Замечательные пределы

Первый замечательный предел:

Второй замечательный предел:

Непрерывность функции

Функция f(x) называется непрерывной в точке а, если она определена в точке а или в некоторой окрестности этой точки и =f(a).

Можно сформулировать четыре условия непрерывности:

1. f(x) должна быть определена в окрестности точки а;

2. должны существовать конечные односторонние пределы 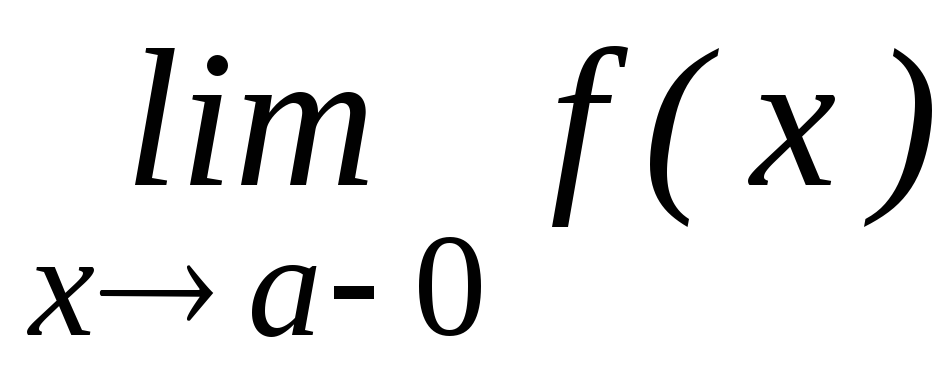и;

3. односторонние пределы должны быть одинаковыми;

4. пределы должны быть равны значению функции в точке а, то есть ==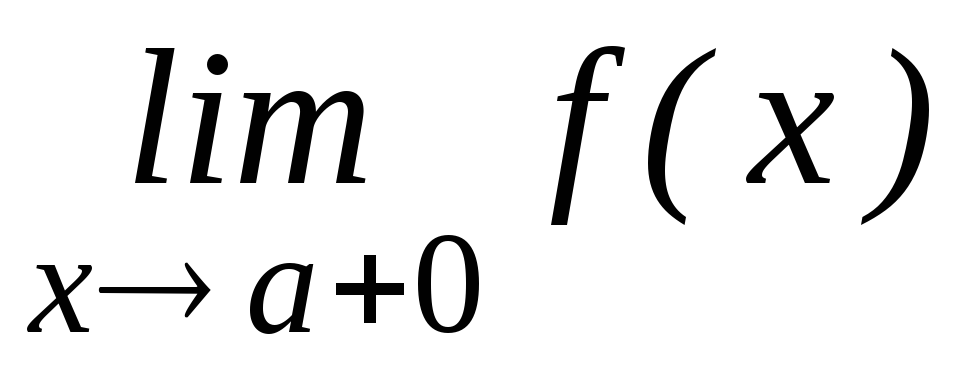f(a).

Функция f(x) называется непрерывной на отрезке [x₁;x₂], если она непрерывна в каждой внутренней точке отрезка, а на границах выполняются условия: =f(x₁), = f(x₂).

Элементарные функции непрерывны во всех точках их области определения.

Разрывы функции

Функция f(x) имеет разрыв в точке а, если она определена слева, и справа от точки а, но в точке а не выполняется хотя бы одно из условий непрерывности.

Различают два основных вида разрыва:

1. Разрывы I рода – а) оба односторонних предела существуют и конечны, но не равны между собой, то есть 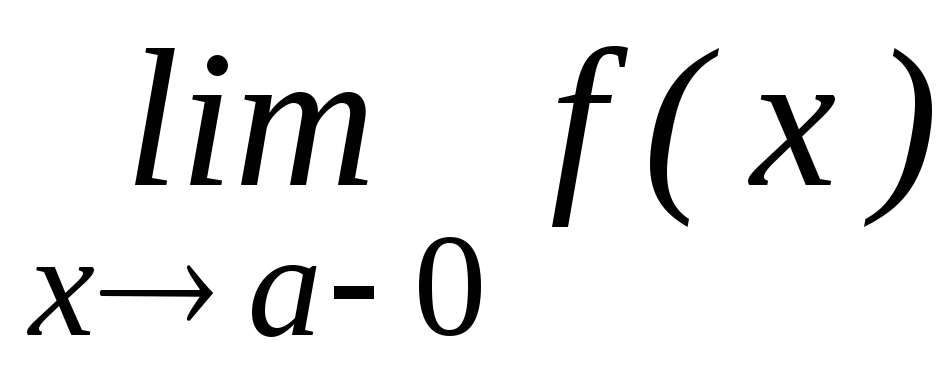≠. Такой разрыв называетсяскачком; б) оба односторонних предела существуют, конечны, равны между собой, но не равны значению функции в точке а, то есть =≠ f(x). Этот предел называется устранимым.

2. Разрыв II рода – хотя бы один из односторонних пределов равен ∞.

_______________

4.2.1. Найти пределы следующих функций: а) ; б); в); г).

Ответ: а) 7; б) 1; в) 1; г) 1.

4.2.2. Раскрыть неопределенность и вычислить пределы:

а) ; б); в); г);

д) ; е).

Ответ: а) -6; б) 1; в) 1/2; г) ; д) 2; е) -1/2.

4.2.3. Раскрыть неопределенность и найти пределы:

а) ; б); в);

г) ; д).

Ответ: а) 1/2; б) -5; в) 0; г) ∞; д) 3.

4.2.4. Раскрыть неопределенности ∞-∞ и 0∞:

а) ; б); в);

г) .

Ответ: а) 1,5; б) 0,5; в) 0; г) -2.

4.2.5. Вычислить пределы:

а) ; б); в); г);

д) ; е); ж);

з) .

Ответ: а) 4; б) 2; в) ; г) 1; д) -1/2; е) 2,25; ж) 1; з) -8.

4.2.6. Найти пределы:

а) ; б); в); г);

д) ; ж).

Ответ: а) е^-5; б) е^-1/3; в) е⁴; г) е²; д) е^-2; ж) е³.

4.2.7. Найти точки разрыва и построить графики функции:

а) ; б); в);

г) .

Ответ: а)II; б) II; в) II; г) I.

4.2.8. Подобрать значения  таким образом, чтобы функции были бы непрерывными:

а) ; б).

Ответ: а) =1; б) не сущ. такого .

_________________

4.2.9. Найти пределы следующих функций:

а) ; б).

Ответ: а) 6; б) 0.

4.2.10. Раскрыть неопределенность :

а) ; б); в);

г) .

Ответ: а) 2/5; б) 4/3; в) 1/20; г) 1,6.

4.2.11. Раскрыть неопределенность :

а) ; б); в);

г) .

Ответ: а) -1/4; б) 2; в) ∞; г) 1/2.

4.2.12. Раскрыть неопределенности ∞-∞ и 0∞:

а) ; б); в); г).

Ответ: а)0; б)0; в)0; г)0.

4.2.13. Найти пределы:

а) ; б); в); г).

Ответ: а) 1/3; б) 8; в) -2; г) 2/5.

4.2.14. Найти пределы:

а) ; б); в); г).

Ответ: а) е⁶; б)е^-3/2 ; в) 1/е²; г)е.

4.2.15. Найти точки разрыва и построить графики функций:

а) ; б); в);

г) .

Ответ: а) II; б) I - устранимый; в) II; г) I – рода.

4.2.16. Найти  таким образом, чтобы следующие функции были непрерывными:

а) ; б).

Ответ: а) =2; б) =16/π.