- •Программа курса
- •Введение Цели и задачи теории автоматического управления
- •Классификация систем автоматического управления
- •Терминология. Основные понятия
- •Математическое описание сау и ее элементов
- •Линеаризация статических характеристик
- •Динамические характеристики звена
- •Свойства преобразования Лапласа
- •Передаточная функция звена
- •Связь оператора s с физикой
- •Частотные характеристики звеньев
- •Логарифмические частотные характеристики лах и лфх
- •Регулярные сигналы
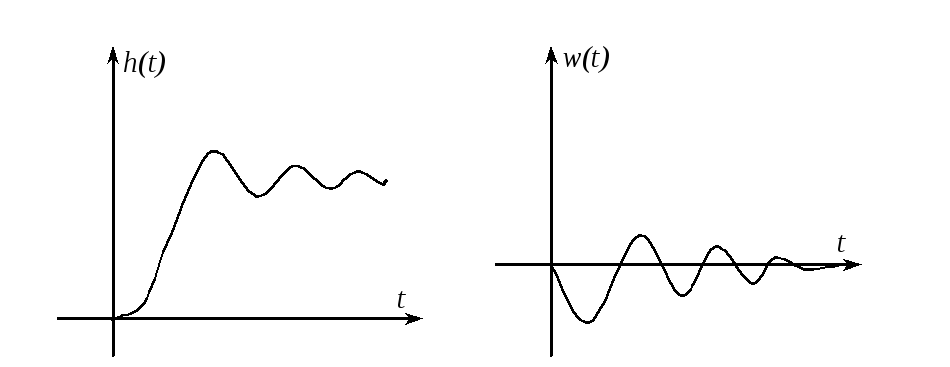
- •Переходная характеристика звена
- •Весовая функция
- •Минимально фазовые и неминимально фазовые звенья
- •Типовые звенья. Характеристики звеньев
- •Идеальное усилительное звено
- •Реальное усилительное звено
- •Идеальное дифференцирующее звено
- •Реальное дифференцирующее звено
- •Интегрирующее звено
- •Форсирующеезвено
- •Квазиинерционное звено
- •Звенья второго порядка. Передаточные функции
- •Частотные характеристики звеньев второго порядка
- •Звено чистого запаздывания
- •Преобразования структурных схем Правила переноса
- •Последовательное соединение звеньев
- •Параллельное соединение звеньев
- •Встречно –параллельное соединение звеньев
- •Замкнутые системы автоматического управления. Виды обратной связи
- •Передаточные функции в системах автоматического управления
- •Передаточная функция разомкнутой системы
- •Устойчивость систем автоматического управления
- •Понятие устойчивости системы
- •Критерии устойчивости
- •Алгебраический критерий устойчивости Раусса. 1875г.
- •Критерий устойчивости Гурвица. 1895 г.
- •О критическом коэффициенте усиления
- •Частотные критерии устойчивости
- •Принцип аргумента
- •Критерий устойчивости Михайлова
- •Частотный критерий устойчивости Найквиста
- •Обобщенная формулировка критерия Найквиста
- •Логарифмический критерий устойчивости (Найквиста)
- •О применении критериев устойчивости
- •Свойства систем автоматического управления
- •Структурная устойчивость (неустойчивость)
- •Запас устойчивости
- •Область устойчивости
- •Метод д-разбиения
- •Оценка качества регулирования
- •Показатели качества переходной характеристики
- •Точность в установившихся режимах
- •Интегральные оценки качества
- •Оценка качества переходного процесса по расположению нулей и полюсов передаточной функции
- •Влияние расположения нулей и полюсов на переходную характеристику
Квазиинерционное звено
Имеется две
разновидности квазиинерционного звена,
представленные передаточными функциями
![]() и
и![]() .
В обоих случаях корни полинома знаменателя
передаточной функции (полюса звена) -
положительные. Следовательно, звено
является не минимально фазовым.
.
В обоих случаях корни полинома знаменателя
передаточной функции (полюса звена) -
положительные. Следовательно, звено
является не минимально фазовым.
Для первого звена его АФЧХ:
![]() .
.
Соответственно
ВЧХ и МЧХ:
![]() ,
,![]() .
.
АЧХ:
![]() (такая же, как у инерционного звена).
(такая же, как у инерционного звена).
ФЧХ:
![]() ,
причем
,
причем![]() ,
а
,
а![]() .
Следовательно, фазовая характеристика
поменяла знак по сравнению с фазовой
характеристикой инерционного звена.
.
Следовательно, фазовая характеристика
поменяла знак по сравнению с фазовой
характеристикой инерционного звена.
Для построения АФЧХ звена выполним следующие преобразования:
![]() ,
,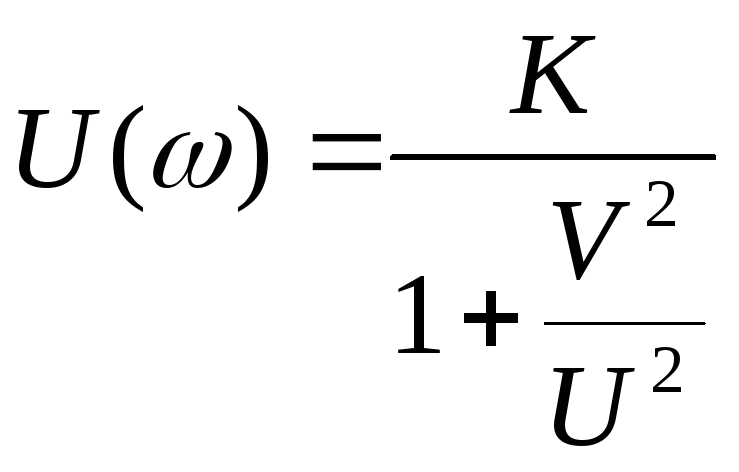 ,
,![]() ,
,
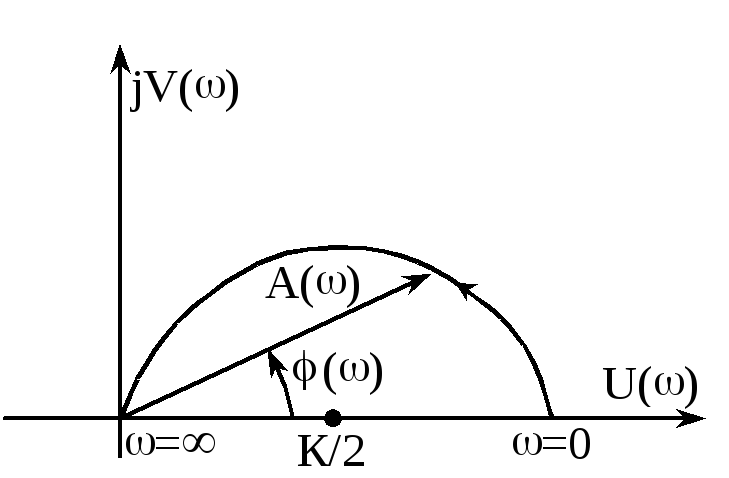
![]() ,
,![]() - получили уравнение окружности. А так
как
- получили уравнение окружности. А так
как![]() и
и![]() ,
то графиком АФЧХ является полуокружность,
расположенная в первом квадранте:
,
то графиком АФЧХ является полуокружность,
расположенная в первом квадранте:
Получим частотные характеристики для второй разновидности квазиинерционного звена.
АФЧХ:
![]() ;
;
ВЧХ:
![]() ;
МЧХ:
;
МЧХ:![]() ;
ФЧХ:
;
ФЧХ:![]()
![]()
![]()
Для построения АФЧХ выполняются аналогичные преобразования:
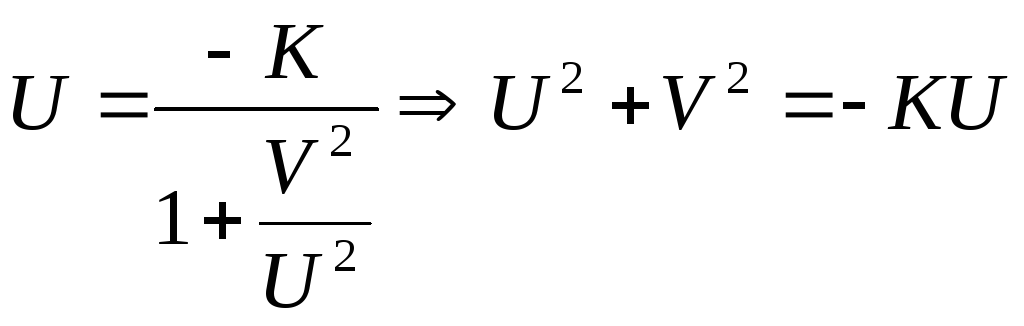 ;
;![]() ;
;![]() .
.
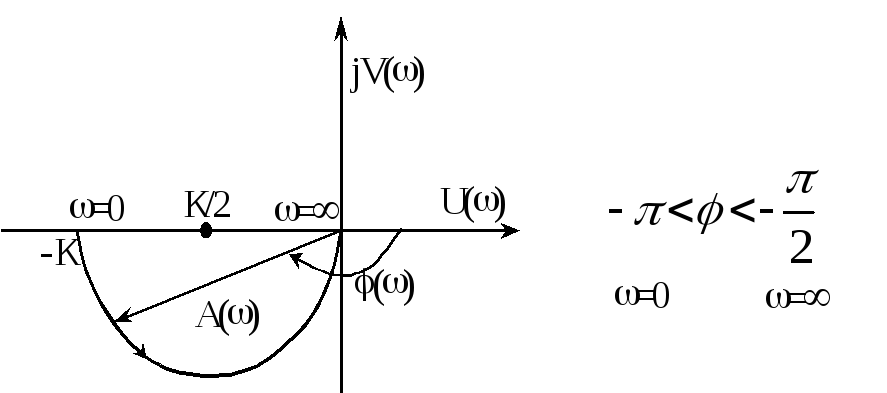
АЧХ:
![]() - совпадает с характеристикой предыдущего
звена и реального усилительного звена.
- совпадает с характеристикой предыдущего
звена и реального усилительного звена.
Звенья второго порядка. Передаточные функции
Математически
модели данных звеньев могут быть
представлены дифференциальным уравнением
![]() и передаточной
функцией
и передаточной
функцией![]() .
.
В зависимости от
величины коэффициентов
![]() это звено может быть апериодическим
второго порядка, колебательным, либо
консервативным.
это звено может быть апериодическим
второго порядка, колебательным, либо
консервативным.
Примером звена второго порядка является RLC-цепочка:
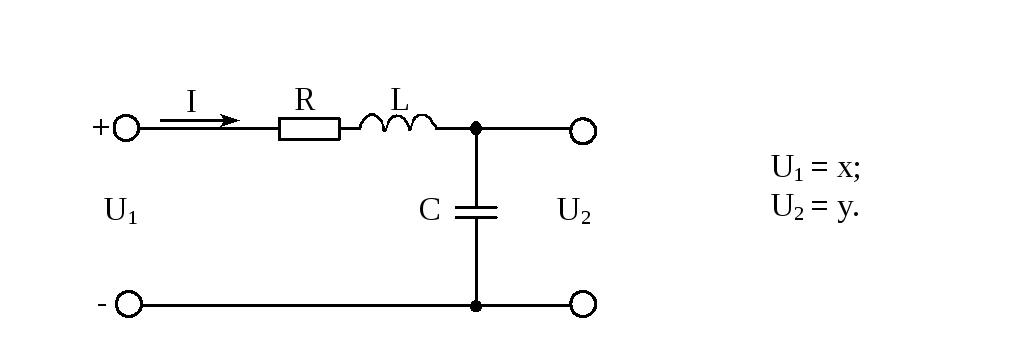 Получим
передаточную функциюRLC-цепочки.
На основании законов Кирхгофа имеем:
Получим
передаточную функциюRLC-цепочки.
На основании законов Кирхгофа имеем:![]() ;
;![]() ;
;![]() .
Далее, после соответствующих подстановок
и преобразований, получаем дифференциальное
уравнение в операторной форме:
.
Далее, после соответствующих подстановок
и преобразований, получаем дифференциальное
уравнение в операторной форме:![]() и передаточную функцию:
и передаточную функцию:
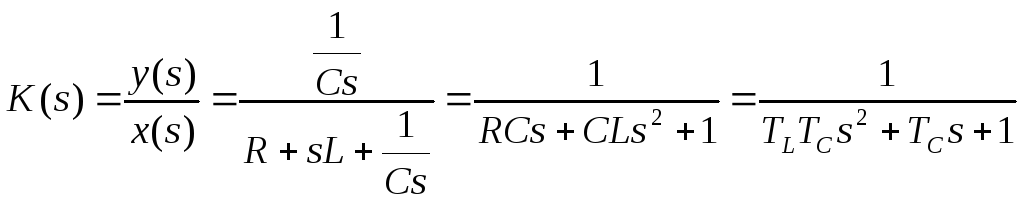 .
.
где постоянные
времени
![]()
![]() .
.
Другим примером может служить двигатель постоянного тока независимого возбуждения

Если составить уравнение якорной цепи и уравнение движения:
![]() ,
,![]()
![]() ;
;![]() ,
то можно получить передаточную функцию:
,
то можно получить передаточную функцию:
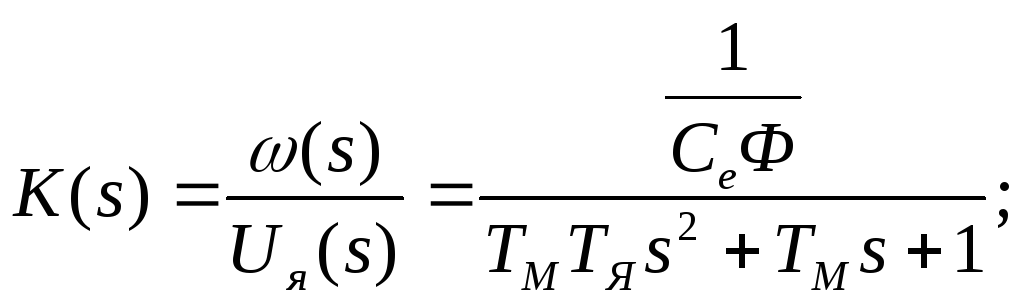 где
где![]()
![]() .
.
В зависимости от постоянных времени ТмиТядвигатель может являться либо колебательным, либо апериодическим звеном второго порядка:
Если ![]() ,
то звено апериодическое 2 порядка;
,
то звено апериодическое 2 порядка;
Если
![]() ,
- колебательное звено;
,
- колебательное звено;
Если ![]() ,
- граничный случай.
,
- граничный случай.
Представим передаточную функция звена второго порядка в виде:
![]() где
где ![]() ;
;
![]() .
.
Характеристическое
уравнение (смотри знаменатель передаточной
функции):
![]() ,
корни которого:
,
корни которого: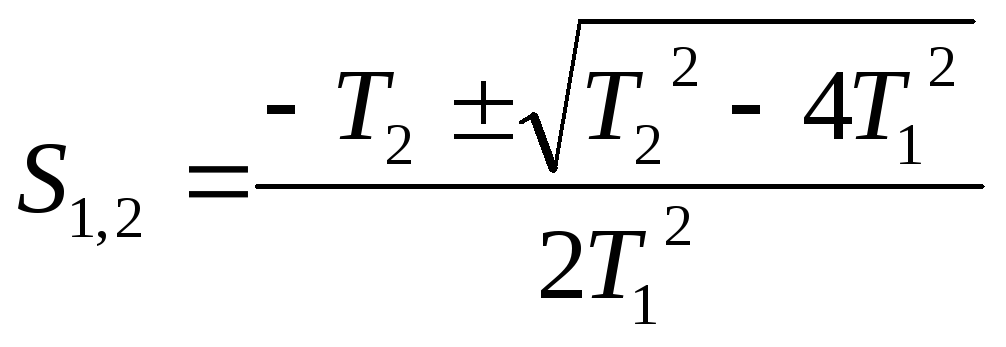 .
.
Если постоянные таковы, что
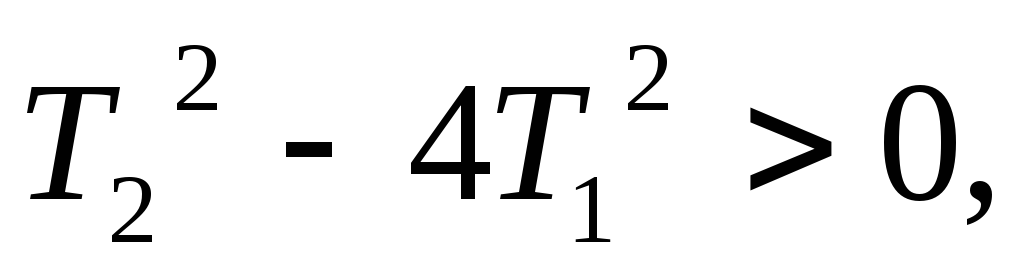
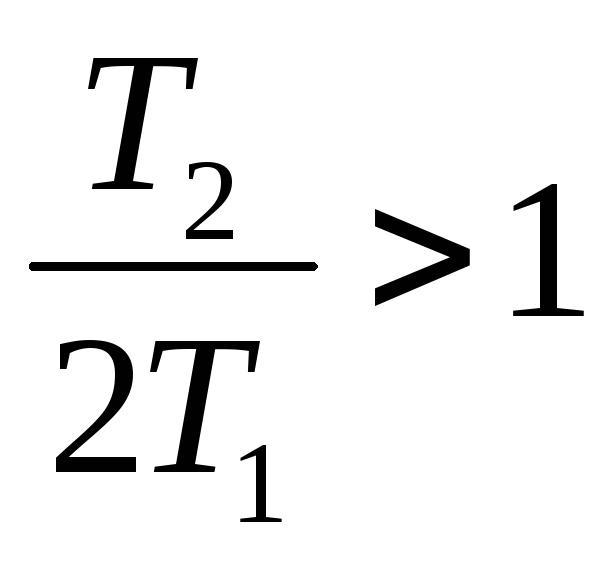 ,
то корни
,
то корни .
Такому звену соответствует апериодическое
движение 2 порядка. Передаточная функция
трансформируется к виду:
.
Такому звену соответствует апериодическое
движение 2 порядка. Передаточная функция
трансформируется к виду: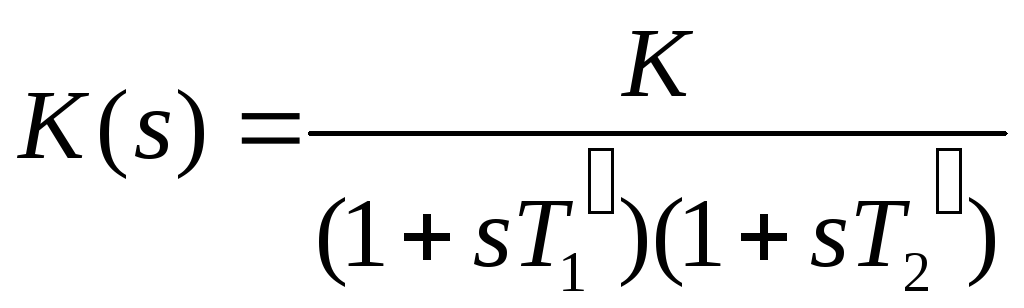 .
.Если
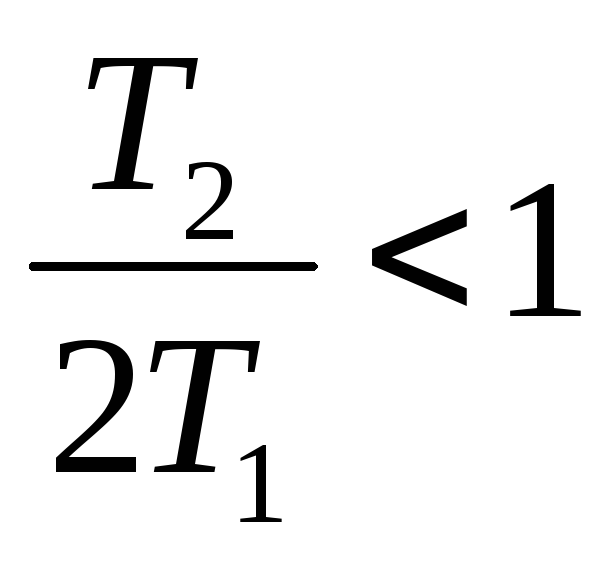 ,
тогда корни
,
тогда корни - движение колебательное.
- движение колебательное.Если
 - граничный случай:
- граничный случай: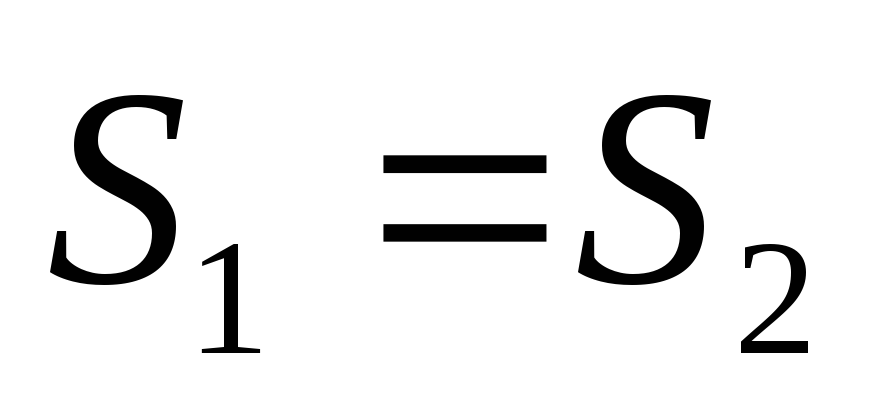 .
.Если
 ,
- консервативное звено. Физически это
означает, что в данном звене отсутствует
рассеяние энергии. Звено теряет свойство
диссипативности. При этом
,
- консервативное звено. Физически это
означает, что в данном звене отсутствует
рассеяние энергии. Звено теряет свойство
диссипативности. При этом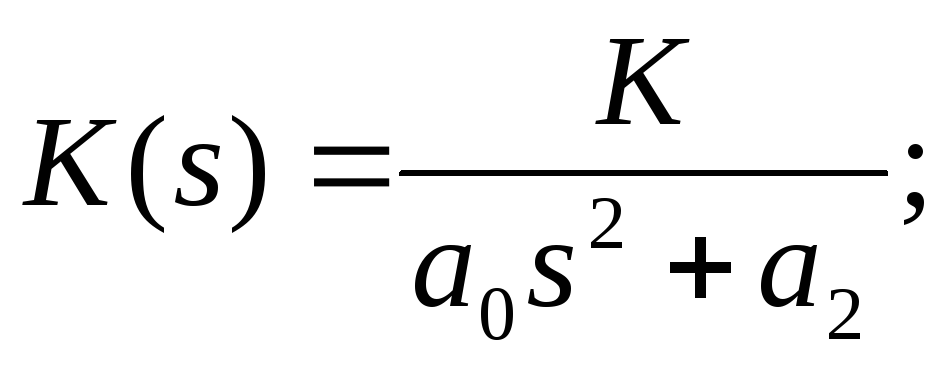
 .
.
Передаточную функцию колебательного звена можно привести к виду:
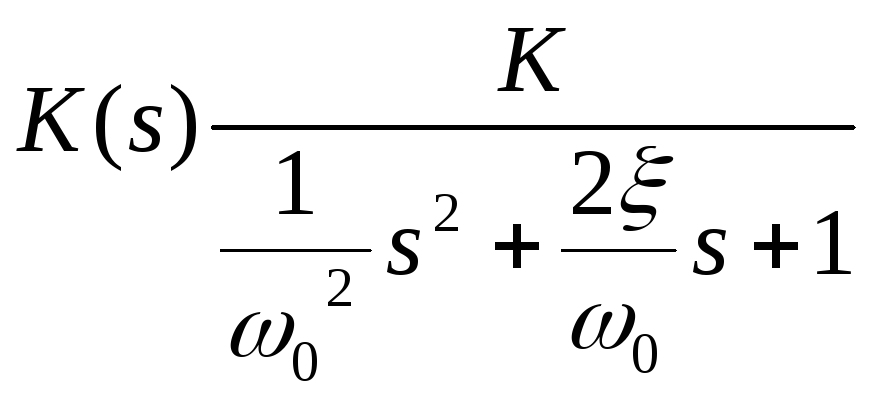 ,
,
где
![]() - частота собственных, недемифированных
колебаний (при
- частота собственных, недемифированных
колебаний (при![]() ).
).
![]() ,
откуда
,
откуда![]() ,
,![]() - коэффициент затухания.
- коэффициент затухания.
1) 0 < <1 - звено колебательное.
2) > 1 - апериодическое звено.
Частотные характеристики звеньев второго порядка
АФЧХ:
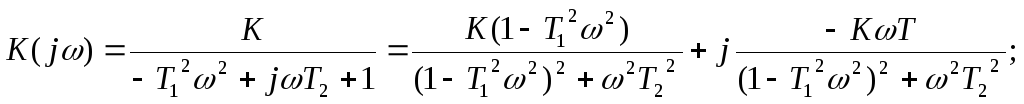
ВЧХ:
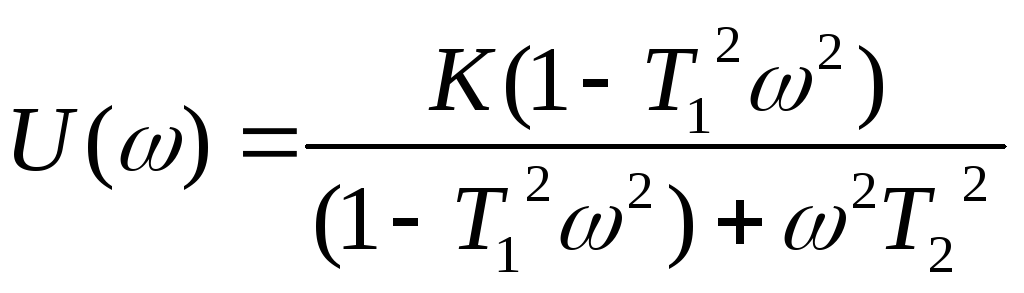 ;
МЧХ:
;
МЧХ: ![]() ;
;
АЧХ:
 ;
;
ЛАХ:
![]() .
.
Ниже приводится изображение частотных характеристик


Для построения логарифмической амплитудной характеристики рассматриваются области частот:
Н.
Ч. ![]()
![]()
![]() ;
;
![]() .
.
В.
Ч. ![]() ;
;
![]() ;
;
![]() .
.
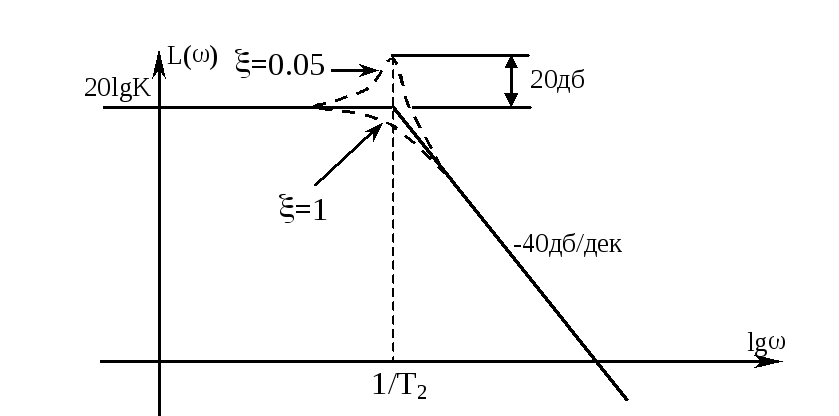
А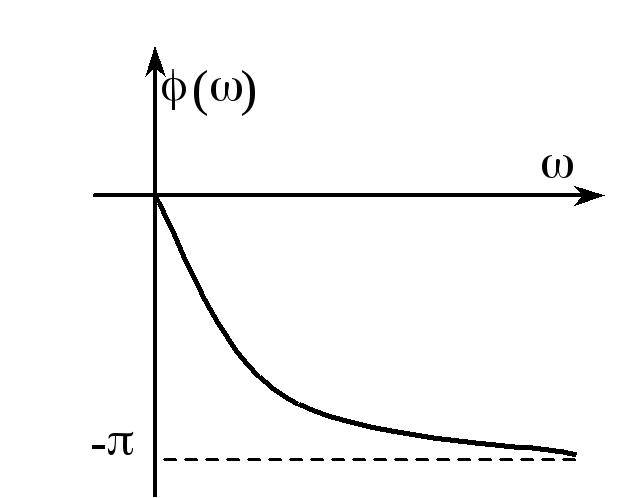 симптотической
ЛАХ пользоваться нельзя. Очень велика
погрешность. При=1
она составляет 6 дб. На практике пользуются
нормированными кривыми поправок
(добавок).
симптотической
ЛАХ пользоваться нельзя. Очень велика
погрешность. При=1
она составляет 6 дб. На практике пользуются
нормированными кривыми поправок
(добавок).
ФЧХ:
 ,
,
 ,
,
![]() при
< 1/T1,
при
< 1/T1,
![]() при
> 1/T1.
при
> 1/T1.
ЛФХ: Логарифмическую фазовую характеристику, как и амплитудную, также можно брать нормированную (из соответствующего справочника):
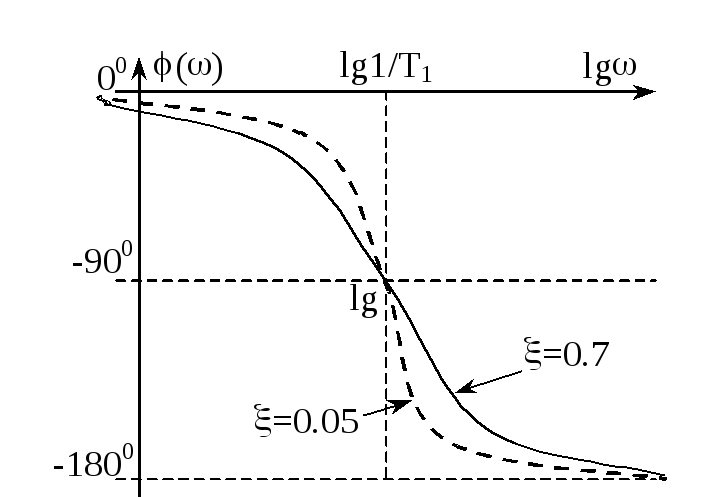
Переходная характеристика звена:
![]() ℒ-1
ℒ-1 .
.
Весовая функция звена определяется путем дифференцирования переходной характеристики.