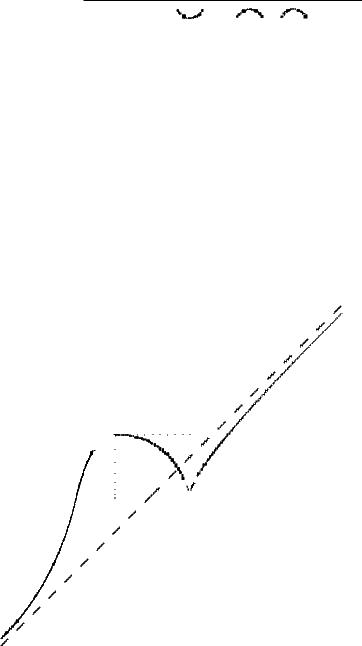
точка x = −1 — точка перегиба заданной функции.

Полученные результаты объединим в таблицу и нарисуем график:

4.13Задания для самостоятельной работы

1.Пусть функция f дифференцируема в точке a, а функция g не дифференцируема в точке a. Доказать, что функция f + g не дифференцируема в точке a. Показать на примерах, что функция f · g может быть как дифференцируемой, так и не дифференцируемой в точке a.

2.Пусть функции f и g не являются дифференцируемыми в точке a. Показать на примерах, что функции f + g и f · g могут быть как дифференцируемыми, так и не дифференцируемыми в точке a.

134

3.Привести пример функции f, которая не дифференцируема в точке a, а функция f2 дифференцируема в точке a.

4.Привести пример такой функции f, что функции f и f2 не является дифференцируемыми в точке a, а функция f3 является дифференцируемой в точке a.

5.Привести пример функции f, которая определена на R и не является дифференцируемой в каждой точке a R, а функция f2 является дифференцируемой в каждой точке a R.

6.Привести пример такой функции f, которая является непрерывной, но не дифференцируемой функцией в точке a, а любая функция fn, n N, n ≥ 2, является дифференцируемой в точке a.

7.Может ли в точке a быть дифференцируемо частное f/g, если

(a)f и g не являются дифференцируемыми в точке a,

(b)f дифференцируема в точке a, а g — нет,

(c)g дифференцируема в точке a, а f — нет.

8.Привести пример функций g : X → Y и f : Y → R таких, что функция g не имеет производной в точке a X, функция f является дифференцируемой точке b = g(a) Y , а суперпозиция f ◦ g дифференцируема в точке a.

9.Привести пример функций g : X → Y и f : Y → R таких, что функция g является дифференцируемой точке a X, функция f не имеет производной в точке b = g(a) Y , а суперпозиция f ◦ g дифференцируема в точке a.

10.Пусть X = (−δ, +δ), δ > 0, функция f является чётной и дифференцируемой в точке x = 0. Доказать, что f0(0) = 0.

11. Пусть X = (−δ, +δ), δ > 0, функция f является дифференцируемой в точке x = 0. Доказать, что если f — чётная функция, то f0 — нечётная функция, если f — нечётная функция, то f0 — чётная функция.

12.Привести пример монотонной и дифференцируемой на R функции, производная которой является периодической функцией.

13.Доказать, что производная периодической, дифференцируемой на R функции, является периодической функцией.

14.Доказать приведённые ранее формулы вычисления производных n-го порядка функций abx+c, sin(ax + b), cos(ax + b).

135

15.Выразить производные до 3-го порядка включительно обратной функции x = f−1(y) через производные функции f(x).

16.Выразить производные fx002 , fx0003 для параметрически заданной функции f : x = ϕ(t), y = ψ(t), t T , если функции ϕ, ψ трижды дифференцируемы на промежутке T .

дважды дифференцируема в точке x = 0?

18. Доказать, что функция f(x) = e−1/x2 , x 6= 0, дифференцируема в

0, x = 0,

точке x = 0 любое число раз, вычислить f(k)(0), k N0.

19. Пусть функция f дважды дифференцируема в точке x0, f(x0) = 0, f0(x0) = 0, f00(x0) 6= 0. Доказать, что в точке x0 функция

f(x) = f(x), x ≥ x0−f(x), x < x0

имеет первую производную, но не имеет второй производной.

20.Пусть функция f имеет первую производную в R и для всех x R f0(x) = c f(x). Доказать, что функция f бесконечно дифференцируема в R и f(n)(0) = cn, если f(0) = 1.

21.Привести пример такой функции f, которая дифференцируема в точке x = 0 любое число раз и последовательность {f(n)(0)} является

(a)ограниченной,

(b)неограниченной сверху (снизу), но ограниченной снизу (сверху),

(c)неограниченной и сверху, и снизу,

(d)монотонной,

(e)немонотонной.

22.Пусть функция f дважды дифференцируема на R, и существуют числа a, b, c такие, что a f00(x)+b f0(x)+c f(x) = 0, x R. Доказать, что функция f бесконечно дифференцируема на R.

23. Пусть функция f дифференцируема на сегменте [a, b], и f0(x) 6= 0 для всех x (a, b). Применимы ли к функции f теоремы Ролля 4.10 и Ферма 4.8?

136

24. Применима ли на сегменте [−1, 1] теорема Лагранжа 4.11 к функциям

25.Применима ли на −π2 , π2 # теорема Коши 4.14 к функциям sin x, x3?

26.Применима ли на сегменте [−1, 1] теорема Ролля к функции |x|?

27.Пусть функция f дифференцируема на интервале (a, b), a, b R и существуют равные конечные пределы f(a + 0) = f(b − 0). Доказать, что существует такая точка γ (a, b), что f0(γ) = 0.

28.Привести пример функции f, которая удовлетворяет условиям теоремы Ролля на сегменте [0, a] и имеет на нём бесконечно много точек γ, в которых f0(γ) = 0.

29.Привести пример функции f, которая удовлетворяет условиям теоремы Ролля на сегменте [a, b] и существует такой сегмент [α, β] [a, b], что f0(x) = 0, x [α, β].

f(x) − ϕ(x) = ax + b.

32.Доказать, что между двумя вещественными корнями многочлена с вещественными коэффициентами всегда лежит вещественный корень его производной.

Доказать, что существует точка γ (a, b), что f(n)(γ) = 0.

34. Пусть функция f непрерывна на промежутке [a, +∞), дифференцируема на интервале (a, +∞), и f(a) < 0, f0(x) ≥ p > 0 для всех x (a, +∞). Доказать, что если уравнение f(x) = 0 имеет на (a, +∞) вещественный корень, то он единственен.

35.Пусть функция f дифференцируема на конечном интервале (a, b) и функция f0 ограничена на нём. Доказать, что функция f ограничена на (a, b) и равномерно непрерывна на нем.

137

36. Пусть функция f дифференцируема на интервале (a, +∞), a > 0 и

37.Пусть функции f и ϕ непрерывны на [a, b] и дифференцируемы на интервале (a, b), f(a) = ϕ(a) и f0(x) > ϕ0(x) для всех x (a, b). Доказать, что f(x) > ϕ(x) для всех x (a, b).

38.Пусть f(x) = xn + px + q, n — четное число. Доказать, что уравнение f(x) = 0 не может иметь более двух разных действительных корней.

39.Пусть f(x) = xn + px + q, где n–нечетное число (n > 1). Доказать, что уравнение f(x) = 0 не может иметь более трех разных действительных корней.

40.Пусть функция f непрерывна на отрезке [1, 2] и дифференцируема на интервале (1, 2). Доказать, что существует такая точка c (1, 2),

что f(2) − f(1) = c2 f0(c). 2

41.Пусть функции f и g непрерывны на [a, b], f(a) < g(a), f(b) > g(b). Доказать, что существует точка c (a, b) : f(c) = g(c).

42.Пусть функция f C[a, b], дважды дифференцируема на промежутке [a, b) и f0(a) = 0. Доказать, что существует точка c (a, b) такая, что

|f(b) − f(a)| ≤ |f00(c)|.

(b − a)2

43. Пусть функция f Cm[a, b], g Cn[a, b], n ≥ 2 и

f(a) = f0(a) = · · · = f(m−1)(a) = 0,

g(a) = g0(a) = · · · = g(n−1)(a) = 0, g(n)(a) 6= 0.

138

46.Пусть функция f n-раз (n > 2) дифференцируема в точке a. Напишите формулу Тейлора для функций f0, f00.

47.С помощью формулы Тейлора доказать, что точка x = 1 является корнем кратности 3 для многочлена p(x) = x5 −x4 −2x3 + 2x2 + x −1.

48.Доказать, что точка a является корнем кратности k ≤ n для многочлена p(x) степени n, тогда и только тогда, когда

при x → a, где Pn(x) — многочлен степени n (n ≥ 2), не следует существования f(n)(a).

139