2. Напряженность поля в диэлектрике. Поляризованность.

При помещении диэлектрика во внешнее поле он поляризуется, то есть приобретает отличный от нуля дипольный момента

,

где - дипольный момент всего диэлектрика,- дипольный момент одной молекулы. Для количественного описания поляризации диэлектрика пользуются векторной величиной – поляризованностью, определяемой как дипольный момент единицы объема диэлектрика

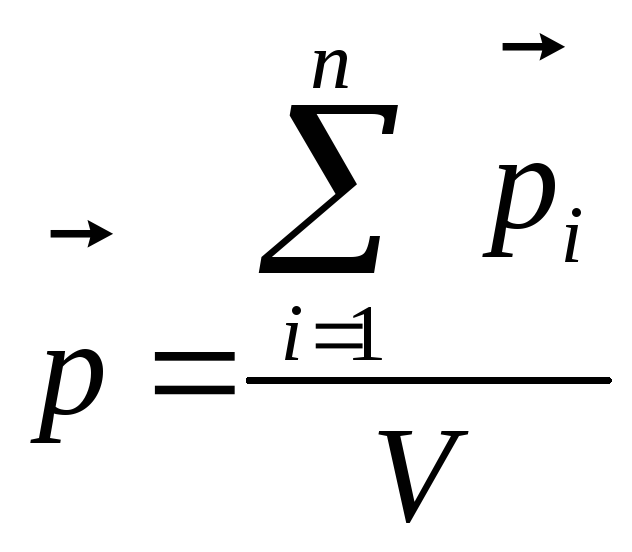, (1)

где - объем диэлектрика,- число молекул в объеме.

Для всех диэлектриков (за исключением сегнетоэлектриков) поляризованность линейно зависит от напряженности поля, еслине слишком велико,

, (2)

где - диэлектрическая восприимчивость вещества.

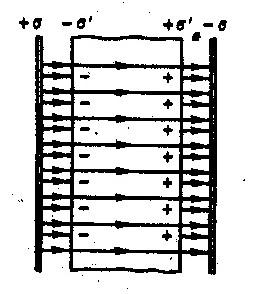
Для установления количественных закономерностей поля в диэлектрике внесем в однородное поле пластинку из диэлектрика. Под действием поля весь диэлектрик поляризуется. Положительные заряды смещаются по полю, отрицательные – против поля. В результате на правой грани будет избыток положительных зарядов, на левой – отрицательных зарядов. Заряды, появляющиеся в результате поляризации называются связанными.

	Концентрация связанных зарядов меньше, чем свободных, поэтому поле создаваемое связанными зарядамине полностью компенсирует поле, создаваемое свободными зарядами. Часть линий напряженности пройдет сквозь диэлектрик, другая часть оборвется на связанных зарядах. Поле, которое будет устанавливаться в диэлектрике равно:
Рис.3.

,

где (поле, создаваемое двумя бесконечными плоскостями). Тогда

. (3)

Определим поверхностную плотность связанных зарядов .Полный дипольный момент пластины диэлектрика равен

, (4)

где - поляризованность диэлектрика,- объем диэлектрика,- площадь грани пластины,- ее толщина.

Дипольный момент пластины можно еще определить как произведение связанного заряда каждой грани на расстояние между ними.

. (5)

Из сравнения (4) и (5) получаем, что

. (6)

Поверхностная плотность связанных зарядов равна поляризованности . Подставив (6) в (3) и учитывая (2) получим

.

Отсюда следует

, (7)

где - диэлектрическая проницаемость среды, показывающая во сколько раз поле ослабляется за счет диэлектрика.

3. Электрическое смещение. Теорема Остроградского-Гаусса для электростатического поля в диэлектрике.

Согласно принципу суперпозиции полей, напряженность поля в диэлектрике равна геометрической сумме напряженностей полей свободных и связанных зарядов

.

Теорема Остроградского-Гаусса для электростатического поля в вакууме может быть распространена на электростатическое поле в среде, если под понимать алгебраическую сумму всех свободных и связанных зарядов, охватываемых замкнутой поверхностью.

(8)

(9)

Подставим (9) в (8)

-

или

.

В обоих интегралах интегрирование проводится по одной и той же замкнутой поверхности . Поэтому

Вектор

(10)

называется электрическим смещением. Размерность [D]=Кл/м ². Тогда теорема Остроградского-Гаусса для электростатического поля в диэлектрике запишется в форме

. (11)

Поток электрического смещения электростатического поля сквозь произвольную замкнутую поверхность, проведенную в поле, равен алгебраической сумме свободных зарядов, охватываемых этой поверхностью.

При расчете полей в среде удобней пользоваться электрическим смещением , так как оно в отличие от напряженности поляне испытывает скачкообразные изменения при переходе через границу диэлектриков.