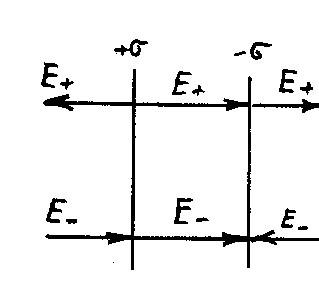
2. Поле двух бесконечных параллельных разноименно заряженных поверхностей.

Плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями +и -. Поле таких плоскостей найдем как суперпозицию полей,

	создаваемых каждой из плоскостей в отдельности (см. рис.4. ). Верхние стрелки соответствуют полю от положительно заряженной поверхности, нижние – от отрицательной поверхности. В области между плоскостями напряженности полей имеют одинаковые направления и складываются, . Вне плоскости – разные и они в сумме дают ноль.
Рис. 4.

3. Поле равномерно заряженной сферической поверхности.

Сферическая поверхность радиуса с общим зарядомзаряжена равномерно с поверхностной плотностью. Поле будет обладать сферической симметрией. Линии напряженности направлены радиально. Построим мысленно сферу радиуса, имеющую общий центр с заряженной сферой.

Рис. 5.	Рис. 6.

Если , то внутрь поверхности попадает весь заряд, тогда по теореме Остроградского-Гаусса

.

Откуда

,

при .

При поле убывает с расстоянием как у точечного заряда. Если, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной поверхности электрическое поле отсутствует. График зависимостиотприведен на рис. 6.

4. Поле равномерно заряженного бесконечного цилиндра (нити).

Бесконечный цилиндр радиуса заряжен равномерно с линейной плотностью,- заряд расположенной на длине. Линии напряженности направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно цилиндра.

	В качестве замкнутой поверхности мысленно построим коаксиальный с заряженным цилиндр радиуса и высотой. Поток векторасквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а поток сквозь боковую поверхность равен. По теореме Остроградского – Гаусса , привеличина=, откуда,.
Рис. 7.

Если , то замкнутая поверхность зарядов не содержит, поэтому поле внутри заряженного цилиндра равно нулю (=0).

Лекция 3

1. Работа по переносу заряда в электростатическом поле. Потенциал поля.

Рассмотрим поле, создаваемое точечным зарядом . В любой точке этого поля на пробный точечный заряддействует сила. Если зарядперемещать в поле, то сила, приложенная к заряду, будет совершать над ним работу (см. рис.).

	При перемещении заряда из точки поля 1 в точку поля 2, сила, действующая на пробный заряд, будет меняться. Рассмотрим перемещение заряда на бесконечно малом участке , где силу можно считать постоянной. Тогда работа ,
Рис.1.

или

.

Работа при перемещении заряда из точки 1 в точку 2 равна

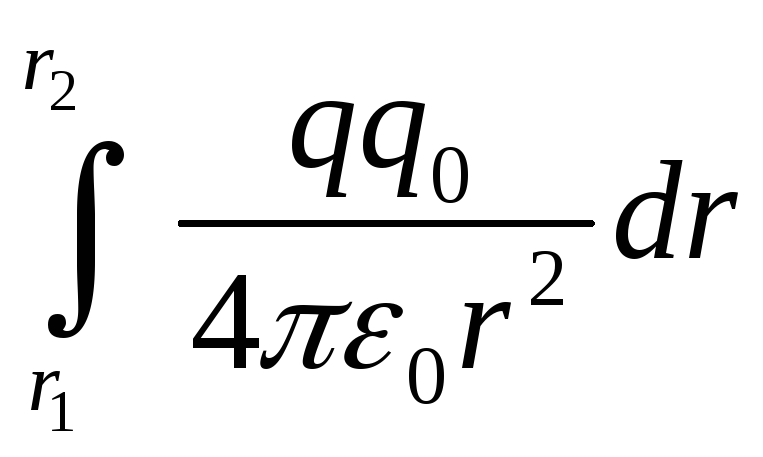^{= = =} (1)

Из формулы (1) видно, что работа по перемещению заряда из точки 1 в точку 2 не зависит от формы траектории, а зависит только от начального и конечного положений заряда в поле. Следовательно, электростатическое поле является потенциальным, как поле силы тяжести.

Работу в потенциальном поле можно представить как разность потенциальных энергий заряда в начальной и конечной точках поля.

(2)

Сопоставление формул (1) и (2) приводит к следующему выражению для потенциальной энергии заряда .

. (3)

Как видно из формулы (3) потенциальная энергия зависит от величины пробного заряда . Разные пробные заряды в одной и той же точке поля будут обладать различными потенциальными энергиями. Однако отношениебудет одинаковым для всех пробных зарядов и может служить характеристикой самого поля. Величина

(4)

Называется потенциалом поля в данной точке.

Физическая величина, являющаяся энергетической характеристикой поля и численно равная отношению потенциальной энергии пробного заряда, помещенного в рассматриваемую точку поля, к этому заряду называется потенциалом поля.

Потенциал величина скалярная.

Из формулы (4) видно, что потенциал численно равен потенциальной энергии, которой обладал бы в данной точке поля единичный положительный заряд.

Потенциал, создаваемый точечным зарядом равен

,

где - расстояние от зарядадо точки поля, где определяется потенциал.

Рассмотрим поле, создаваемое системой точечных зарядов . Работа, совершаемая силами этого поля над пробным зарядом, будет равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности в силу принципа суперпозиции.

, (5)

где

, (6)

- расстояние от зарядадо начального положения заряда,- расстояние от зарядадо конечного положения заряда.

Подставим (6) в (5). Тогда

^- (7)

и потенциальная энергия заряда в поле системы зарядов будет равна

, (8)

а потенциал поля, создаваемый системой точечных зарядов

. (9)

Потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.

Напряженности складываются при наложении полей векторно, а потенциалы – алгебраически. Поэтому вычисление потенциалов намного проще, чем вычисление напряженностей поля.

Из определения потенциала следует, что

.

Следовательно, работа сил поля над зарядом может быть выражена как

. (10)

Работа, совершаемая над зарядом силами поля равна произведению этого заряда на разность потенциалов в начальной и конечной точках.

Если заряд, находящийся в точке с потенциалом , удаляется на бесконечность (где по условию потенциал равен нулю), работа сил поля равна

, а. (11)

Потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки поля на бесконечность.

Из формулы (11) можно установить единицу измерения потенциала [] = Дж/Кл = В.

1В – потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией в 1Дж.