Лекция 1 Электростатика

1. Закон сохранения электрического заряда.

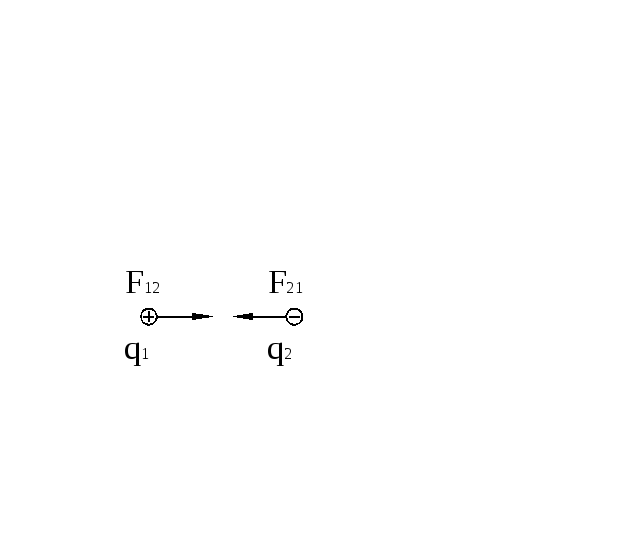
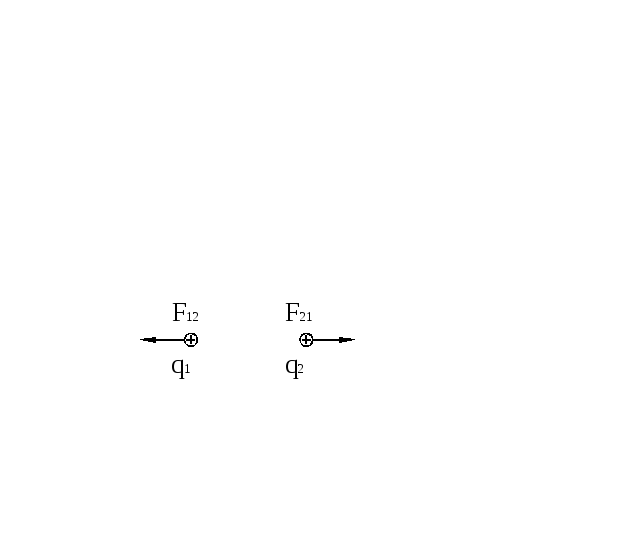
В природе существуют два рода электрических зарядов: положительные и отрицательные. Положительные заряды возникают на стекле, натертом кожей, отрицательные – на янтаре или эбоните, натертых шерстью. Разноименные заряды притягиваются, одноименные – отталкиваются. Электрический заряд любой системы состоит из целого числа элементарных зарядов равных 1,6 10^-19Кл. Отрицательный элементарный заряд имеет электрон, масса которого 9,11 10^-31кг. Наименьшая по массе частица с положительным элементарным зарядом –протон, ядро атома водорода. Масса протона – 1,67^10-27кг.

Античастица позитрон имеет такую же массу как и электрон и положительный элементарный заряд.

Система тел или частиц называется электрически изолированной, если между ней и внешними телами нет обмена электрическими зарядами.

Из обобщения опытных данных установлен фундаментальный закон сохранения электрического заряда: алгебраическая сумма электрических зарядов, образующих электрически изолированную систему, не изменяется при любых процессах, происходящих в этой системе.

В системе могут образоваться электроны за счет ионизации атомов и молекул. Однако, сколько образуется электронов – столько и положительных ионов, и сумма зарядов остается постоянной.

2. Закон Кулона.

Сила взаимодействия неподвижных электрических зарядов подчиняется закону, открытому в 1785 году Кулоном.

Сила электростатического взаимодействия двух точечных зарядов, находящихся в вакууме, прямо пропорциональна произведению этих зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль соединяющей их прямой.

Точечным зарядом называется заряд, расположенный на теле, размерами которого можно пренебречь по сравнению с расстояниями до других заряженных тел

,

где - коэффициент пропорциональности, зависящий от выбора системы единиц. В системе СИ,= 8,85 10^-12Кл²/Нм²- электрическая постоянная,=9 10⁹Нм²/Кл²,- заряды,расстояние между зарядами.

Если заряды взаимодействуют в однородной изотропной среде, то закон Кулона имеет вид

,

где - безразмерная величина, диэлектрическая проницаемость среды, показывающая во сколько раз сила взаимодействия между зарядами в среде меньше силы взаимодействия в вакууме,. Для вакуума= 1.

3. Электрическое поле и его напряженность.

Между электрическими зарядами в пространстве действует кулоновская сила. Значит в этом пространстве существует силовое поле. Поле наряду с веществом является одним из видов материи, посредством которого осуществляется взаимодействие между частицами вещества.

Поле, образованное неподвижными электрическими зарядами называется электростатическим.

Силовой характеристикой поля является напряженность .

Физическая величина, являющаяся силовой характеристикой поля и численно равная отношению силы, действующей со стороны поля на точечный пробный положительный заряд, помещенный в рассматриваемую точку поля, к этому заряду.

.

- величина векторная. Пробный заряддолжен быть настолько мал, чтобы не исказить поля.

Сила, действующая со стороны поля на произвольный заряд, помещенный в поле равна , но при этомуже будет характеризовать поле, искажаемое зарядом.

Электрическое поле будет однородным, если во всех точках напряженность будет одинакова по величине и направлению. Напряженность измеряется в Н/Кл или В/м.

Напряженность поля, создаваемая точечным зарядом, легко найти из закона Кулона

где - расстояние от заряда, создающего поле, до точки, где определяется напряженность.

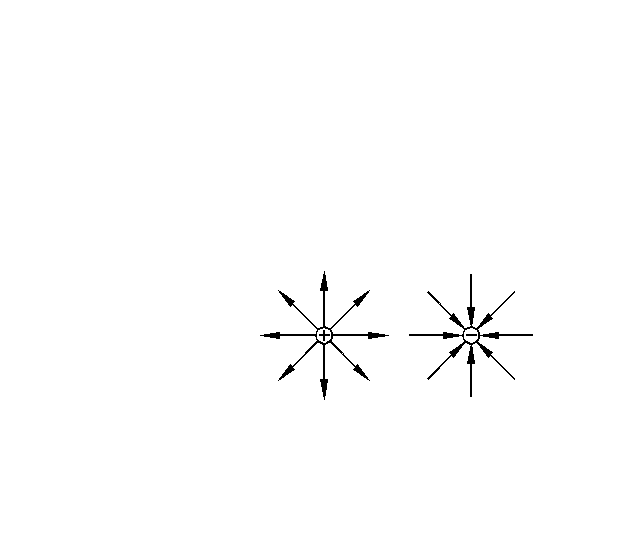
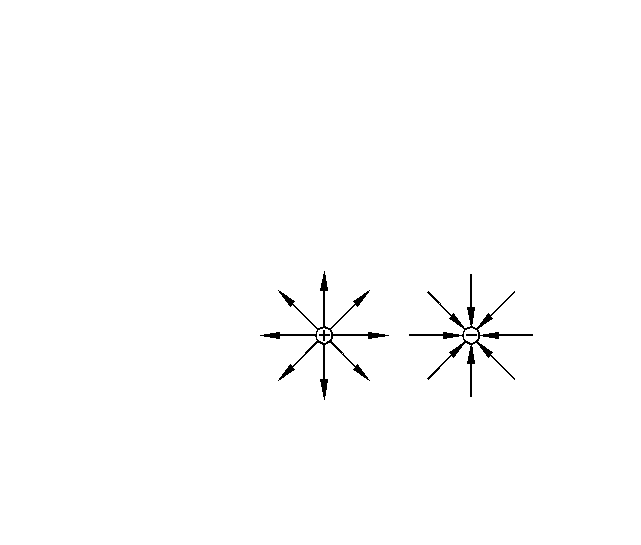
Вектора напряженности для точечного заряда направлены радиально к заряду, если он отрицательный, и от заряда – если он положительный.

Поле, создаваемое точечным зарядом – центральное поле.

Графически изображать поле с помощью векторов напряженности неудобно.

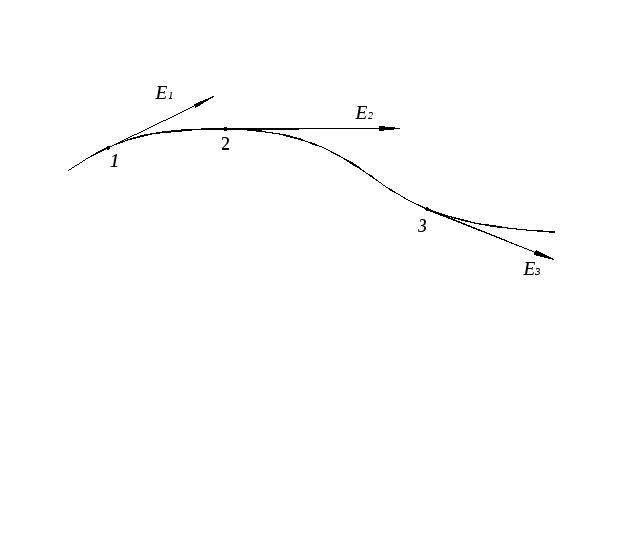
Вектора напряженности накладываются друг на друга. Фарадей предложил изображать поле с помощью силовых линий ( или линий напряженности).Силовыми линиями называются линии, проведенные в поле так, что касательные к ним в каждой точке совпадают по направлению с вектором напряженности поля.

Линия напряженности считается направленной так же, как вектор поля в рассматриваемой точке линии. Например на рассматриваемом рисунке линия напряженности направлена слева направо.

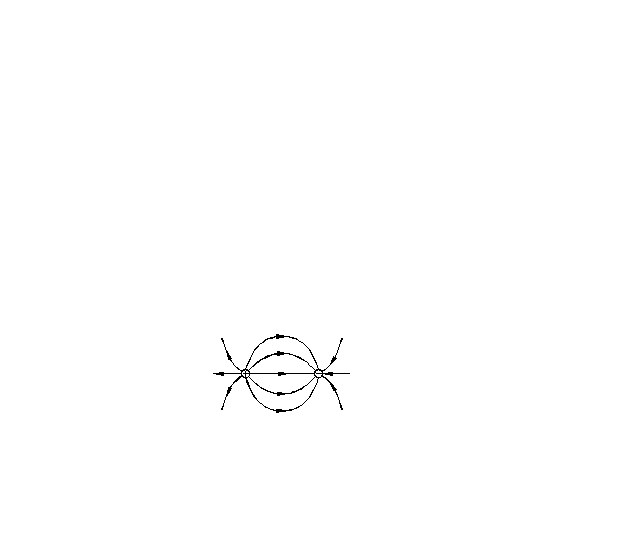
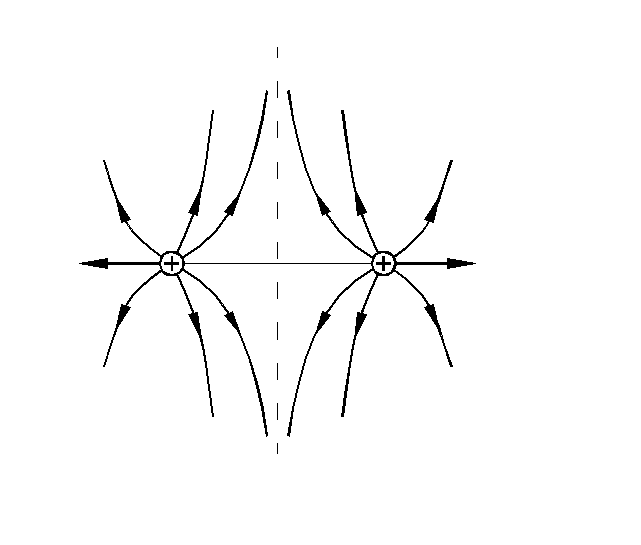
Линии напряженности не пересекаются, так как в каждой точке поля векторимеет только одно направление. Для примера приведем линии напряженности поля, создаваемого двумя точечными зарядами.

Рассмотрим поле, создаваемое системой неподвижных точечных зарядов находящихся в вакууме. Экспериментально было показано, что результирующая сила, действующая на пробный зарядв любой точке поля, равна геометрической сумме сил, приложенных к зарядусо стороны каждого из зарядов

, (1)

где

(2)

и

, (3)

- напряженность поля системы зарядов,

- напряженность поля одногозаряда.

Подставим (2) и (3) в (1) и получим

-

или

=(4)

Уравнение (4) отражает принцип суперпозиции полей (принцип независимости действия электрических полей).

Напряженность электрического поля системы точечных зарядов равна геометрической сумме напряженностей полей каждого из этих зарядов в отдельности.