6. Циркуляция вектора магнитной индукции.

Аналогично циркуляции вектора напряженности электрического поля введем циркуляцию вектора магнитной индукции.

Циркуляцией вектора по заданному замкнутому контуру называется интеграл

.

- вектор элементарной длины, направленный вдоль обхода контура,- составляющая векторав направлении касательной к контуру,- угол между векторами.

Закон полного тока для магнитного поля (теорема о циркуляции вектора ):

Циркуляция вектора по произвольному замкнутому контуру равна произведениюна алгебраическую сумму токов, охватываемых этим контуром.

⁼ ,

- число проводников с током, охватываемых контуромпроизвольной формы.

	Каждый ток учитывается столько раз, сколько он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта. Например, для рисунка 3, =.
Рис.3.

7. Магнитное поле соленоида.

Сравнивая циркуляции ивидим принципиальное различие. Циркуляция электрического поля равна нулю, то есть электростатическое поле потенциально. Работа по замкнутому пути в потенциальном поле равна нулю.

Циркуляция не равна нулю. Такое поле является вихревым. Теорема о циркуляции вектораимеет такое же значение, как теорема Гаусса в электростатике для потока через замкнутую поверхность. Эта теорема позволяет рассчитать индукцию поля без применения закона Био - Савара- Лапласа

	Пусть длина соленоида больше диаметра витка,. Рассчитаем поток векторасквозь соленоид. (см. рис.40. Проведем замкнутый контурсквозь витки соленоида. Внутри соленоида () поле однородно, вне () – неоднородно и очень слабо и им можно пренебречь. Тогда циркуляция векторасквозь замкнутый контурравна ,
Рис.4.

где - угол междуи, внутри соленоида равный нулю,- магнитная проницаемость сердечника внутри соленоида,число витков соленоида,- длина соленоида. Тогда

.

Магнитный поток сквозь один виток соленоида площадью равен

,

А полный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением равен

,

где - индуктивность соленоида.

Отсюда

.

Лекция 11 Магнитное поле в веществе.

1. Магнитные моменты атомов.

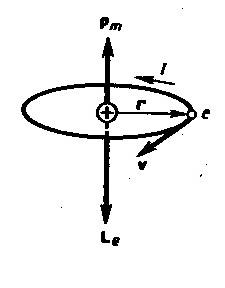
Для объяснения магнитных явлений в веществе рассматривают движение электронов в атоме согласно классической механике. Электрон вращается вокруг ядра по круговой орбите.

	Электрон, движущийся по орбите эквивалентен круговому току и обладает поэтому орбитальным магнитным моментом и модулем, так как- сила тока. - частота вращения электрона,- площадь орбиты. Теперь .
Рис.1.

Направление определяют по правилу буравчика.

Кроме орбитального магнитного момента электрон обладает собственным магнитным моментом – спином . Спин имеет квантовую природу и не имеет аналогов в классике. Общий магнитный момент атома или молекулыравен векторной сумме магнитных моментов (орбитальных и спиновых) входящих в атом электронов

.

Магнитный момент ядра атома в 1000 раз меньше магнитных моментов электронов и они не учитываются.

При попадании вещества в магнитное поле оно намагничивается. Для количественного описания намагничивания вводят векторную величину - намагниченность.

Вектором намагничивания данного вещества называется физическая величина, численно равная магнитному моменту единицы объема

,

- магнитный момент магнетика, равный векторной сумме магнитных моментов отдельных молекул.- измеряется в А/м,- объем магнетика..

Магнитное поле в веществе складывается из двух полей: внешнего поля, создаваемого током, и поля создаваемого намагниченным веществом. Вектор магнитной индукции результирующего поля в магнетике равен векторной сумме магнитных индукций внешнего поля , поля образованного намагничивающим током в вакууме и поля микротоков,

(1)

,

.

Магнитное поле макротока описывается вектором напряженности .

Опыт показывает, что при небольших величина вектора намагничивания в изотропных средах пропорциональна напряженности поля, вызывающего намагничение

,

- магнитная восприимчивость вещества (безразмерная величина).

,

- безразмерная величина представляет собой магнитную проницаемость вещества.

В зависимости от знака и величины восприимчивости все магнетики делятся на три группы:

- диамагнетики ,

- парамагнетики ,

- ферромагнетики .