-
Пропозициональные формулы. Таблицы истинности.
Если формула не содержит кванторов и переменных, то в этом случае она называется пропозициональной формулой или формулой логики высказываний. Другими словами, множество пропозициональных формул можно определить так:
• Пропозициональные (или высказывательные) переменные: X, Y, X1, X2 и т. д. Это простейшие формулы, обозначающие высказывания.
• Если A и B – пропозициональные формулы, то ¬A или A B (− любая пропозициональная связка) также пропозициональные формулы.
• Других способов построения пропозициональных формул нет. Пример: (A ⊃ B∨C) ⊃ (A ⊃ B).
Как следует из соглашения 3, значение пропозициональной формулы полностью определяется конечным набором истинностных значений пропозициональных переменных, из которых она построена. Если таких пропозициональных переменных n, то достаточно перебрать 2n их значений, чтобы выяснить характер зависимости значения формулы от значений ее высказывательных переменных. Систематический перебор всех вариантов значений переменных и вычисление для них значений формулы дает таблицу истинности.
• Оценивание пропозициональной формулы – функция, сопоставляющая всем ее различным элементарным подформулам истину или ложь.
• Таблица истинности – функция, сопоставляющая каждому возможному оцениванию значение формулы при этом оценивании.
Таблица истинности для формулы (A ⊃ B∨C) ⊃ (A ⊃ B).
-
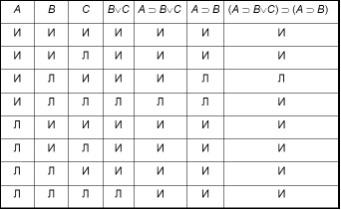
Тавтологии, противоречия и выполнимые формулы. Примеры тавтологий.
• Формула, которая истинна независимо от того, какие значения принимают встречающиеся в ней высказывательные переменные, называется тавтологией (или тождественно истинной формулой). Таким образом, тавтологии – формулы, которые тождественно истинные при любой интерпретации.
• Формула называется выполнимой, если на некотором наборе распределения истинностных значений переменных она принимает значение И.
• Формула называется тождественно ложной или противоречием, если она ложна независимо от того, какие значения принимают встречающиеся в ней высказывательные переменные.
• Формула называется опровержимой, если при некотором распределении истинностных значений переменных она принимает значение Л.
Очевидные следствия данных определений: • A – тавтология тогда и только тогда, когда A не является опровержимой;
• A – тождественно ложна тогда и только тогда, когда A не является выполнимой;
• A – тавтология тогда и только тогда, когда ¬A – тождественно ложна;
• A – тождественно ложна тогда и только тогда, когда ¬A – тавтология;
Важность тавтологий и противоречий для логики в том, что они не зависят от конкретной формализации предметной области.
Избранные важные тавтологии (A, B, C - произвольные формулы):
• A∨¬A (закон исключенного третьего или tertium nondatur);
• A⊃A;
• A ⊃ (B⊃A);
• (A ⊃B) ⊃ ((B⊃C) ⊃ (A⊃C)) (цепное рассуждение);
• (A ⊃ (B⊃C)) ⊃ ((A⊃B) ⊃ (A⊃C));
• (A&B) ⊃A; (A&B) ⊃ B;
• A ⊃ (B ⊃ (A&B));
• A ⊃ (A∨B); B ⊃ (A⊃B);
• (¬B⊃¬A) ⊃ ((¬B⊃A) ⊃ B);
• ((A⊃B) ⊃A) ⊃A (закон Пирса).
Каждую из этих тавтологий можно обосновать, например, составив таблицу и вычислив по ней значение формулы при произвольных значениях A, B и C.