2.5. Естественный способ задания движения точки

Е

Рис. 2.11

стественный способ задания движения точки применяется в случае, когда траектория движения точки заранее известна. Траекторией могут быть как прямая, так и кривая линии (рис. 2.11).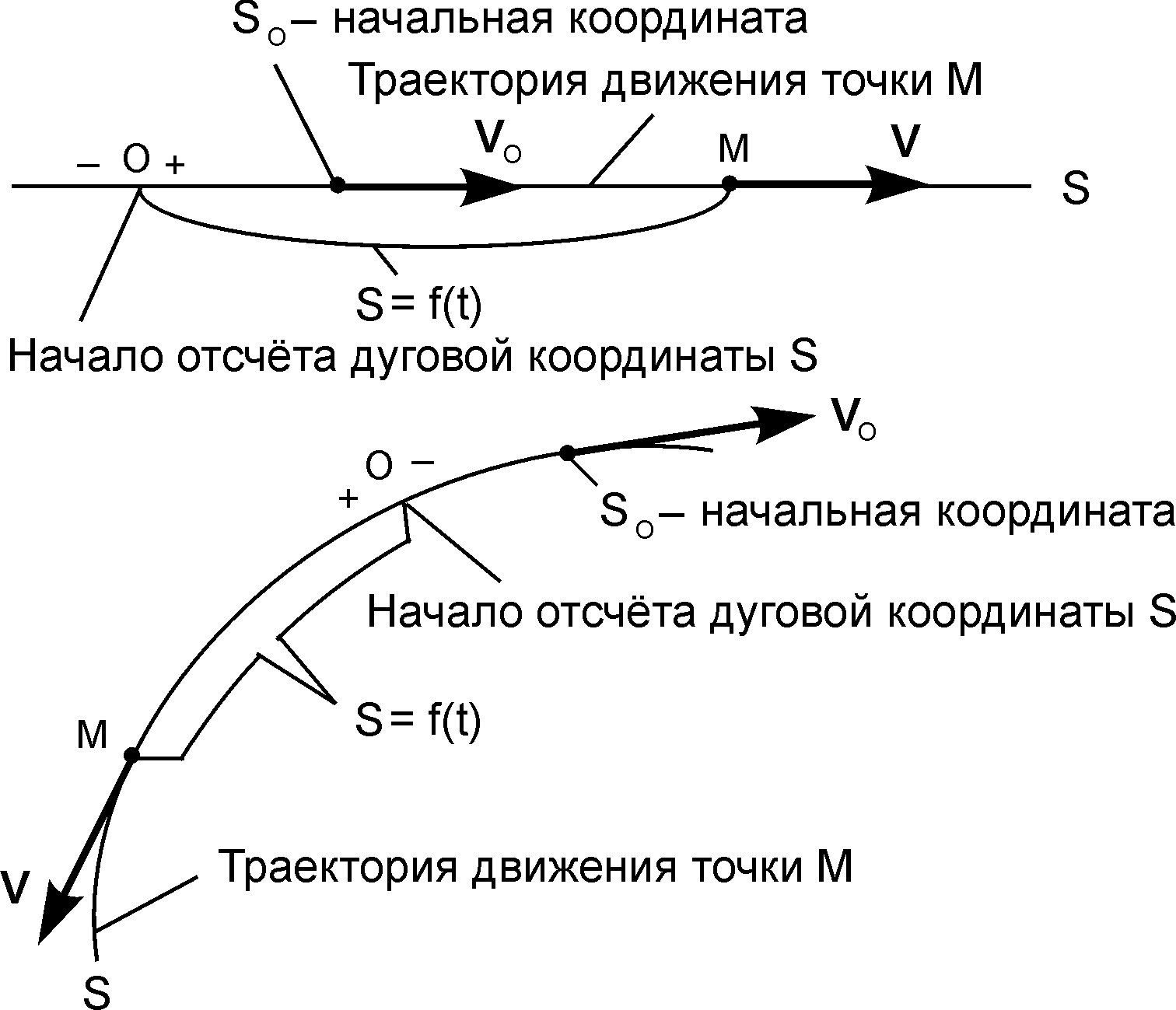

На известной траектории движения точки выбирается неподвижная точка О, которую называют началом отсчёта дуговой координаты. Положение движущейся точки М на траектории определяется дуговой координатой, т. е. расстоянием ОМ = S, отложенным по траектории от начала отсчета О.

Прямую линию на рис. 2.11 можно считать дугой окружности, радиус которой равен бесконечности.

Расстояния, отложенные в одну сторону от точки О, условно считают положительным, а в противоположную сторону – отрицательным, т. е. устанавливается направление отсчета дуговой координаты. При движении точки М расстояние S от этой точки до неподвижной точки О изменяется с течением времени, т. е. дуговая координата S является функцией времени.

S = f(t).

Эту зависимость называют уравнением движения точки в естественных координатах.

Если вид функции S = f(t) известен, то для каждого значения времени t_i можно найти значение дуговой координаты S_i, отложить соответствующее расстояние по траектории от начала отсчета О и указать, где находится движущаяся точка М в этот момент времени.

Таким образом, движение точки определено, если известны следующие элементы: вид траектории движения точки (прямая линия, окружность, эллипс и т. д.); начало отсчёта (точка О) дуговой координаты; положительное и отрицательное (+, –) направления отсчёта дуговой координаты; уравнение движения S = f(t).

Дуговую координату точки не следует смешивать с длиной пути, пройденного точкой за время t.

Пример. Пусть уравнение движения точки имеет вид S = 10·sin(·t) см. При начальном времени t₀ = 0 начальная координата S₀ = 0. При t₁ = 0,5 c S(t₁) = 10 см; при t₂ = 1 c S(t₂) = 0; при t₃ = 1,5 c S(t₃) = – 10 см; при t₄ = 2 c S(t₄) = 0.

Таким образом, за время t₄ = 2 c точка М прошла путь, равный 40 см, а её дуговая координата S₄ в этот момент времени равна нулю.

2.6. Естественные координатные оси

Точка перемещается в пространстве по заданному уравнению движения S = f(t) (рис. 2.12).

Проведём в точке М кривой АВ соприкасающуюся плоскость, нормальную плоскость, перпендикулярную соприкасающейся плоскости, и спрямляющую плоскость, перпендикулярную соприкасающейся и нормальной плоскостям. Пересечением трёх плоскостей образован естественный трёхгранник.

Линию пересечения соприкасающейся и нормальной плоскостей называют главной нормалью.

Линию пересечения спрямляющей и соприкасающейся плоскостей называют касательной.

Линию пересечения спрямляющей и нормальной плоскостей называют бинормалью.

Рис. 2.12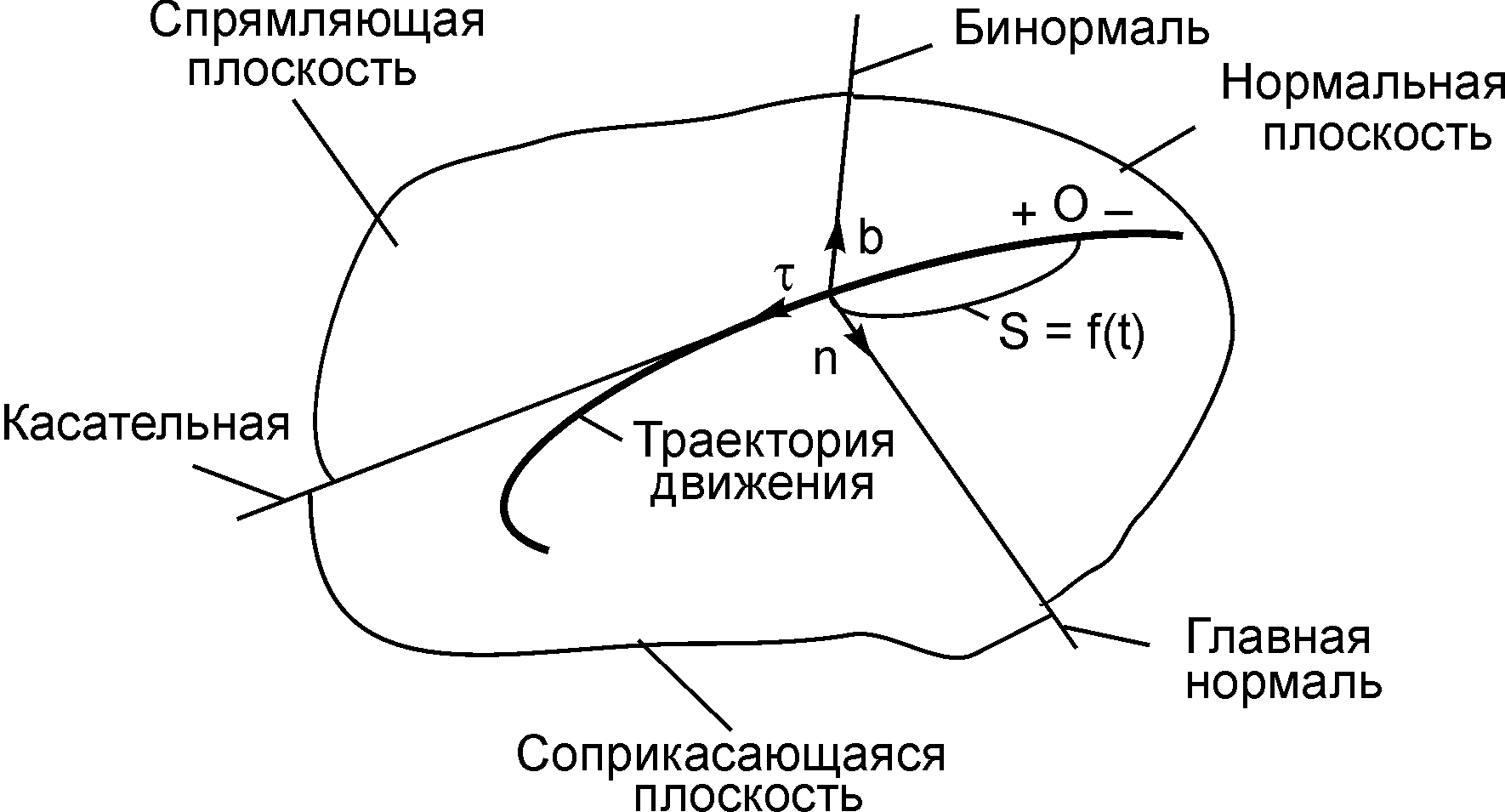

Естественными координатными осями называют три взаимно перпендикулярные оси: касательная (единичный вектор τ всегда направлен в сторону возрастания дуговой координаты S); главная нормаль (единичный вектор n направлен в сторону вогнутости траектории); бинормаль (единичный вектор b перпендикулярен векторам τ и n и направлен так же, как и вектор k по отношению к векторам i, j в правой декартовой системе отсчёта OXYZ) (рис. 2.13).

Рис. 2.13

Если в правой системе отсчёта OXYZ смотреть на единичные векторы I, j с положительного направления оси OZ (навстречу вектору k), то для совпадения направлений векторов i, j вектор i необходимо поворачивать против хода часовой стрелки. По такому же правилу ориентируются в пространстве векторы τ, n, b.

Начало естественных координатных осей всегда располагается в точке (см. рис. 2.12) и при движении по траектории перемещается вместе с ней. Естественные координатные оси, оставаясь взаимно перпендикулярными, изменяют своё направление в пространстве. Следовательно, естественные координатные оси образуют подвижную систему отсчёта (ПСО).

Р

Рис. 2.14

ассмотрим движение точки на плоскостиOXY (рис. 2.14).

На рис. 2.14 орты τ и n расположены в соприкасающейся плоскости, а орт b не виден, так как он перпендикулярен ортам τ и n и плоскости рисунка.

Главная нормаль всегда проходит через центр кривизны траектории движения точки. Здесь ρ – радиус кривизны траектории движения. При движении точки по окружности радиусом R радиус кривизны траектории ρ = R. При движении точки по прямой линии ρ = . В остальных случаях при движении точки по криволинейной траектории радиус её кривизны является переменной величиной.