Раздел второй

2. Кинематика

2.1. Введение в кинематику

Кинематикой называется раздел механики, в котором изучается движение материальных тел в пространстве, вне связи с силами, определяющими это движение.

Механическое движение, т.е. происходящее во времени изменение положения одного тела относительно другого, рассматриваемое в системе отсчёта, которая и связана с этим другим телом.

Система отсчёта может быть как движущейся, так и условно неподвижной. При изучении движений на Земле за неподвижную систему отсчёта (НСО) принимают систему координатных осей, неизменно связанных с Землей. Тело, положение которого по отношению к выбранной системе отсчёта не изменяется, находится в состоянии относительного покоя (по отношению к этой системе отсчёта).

Пространство в механике рассматривается как трёхмерное евклидово пространство. За единицу длины при измерении расстояний принимается метр (м). За единицу времени принимается одна секунда (с). Все кинематические характеристики движения тела (расстояния, скорости, ускорения) рассматриваются как функции времени.

2.2. Координатный способ задания движения точки

Рассматривается движение точки М в неподвижной системе отсчёта OXYZ (рис. 2.1). Единичные векторы (орты) i, j, k показывают положительные направления отсчёта координат X, Y, Z. Движущаяся точка описывает в пространстве некоторую линию, которую называют траекторией движения точки. По виду траектории все движения точки делятся на прямолинейные и криволинейные. Положение точки М в неподвижной системе отсчёта (НСО) определяется тремя координатами X, Y, Z. При движении точки М её координаты изменяются с течением времени. Следовательно, координ

Рис. 2.1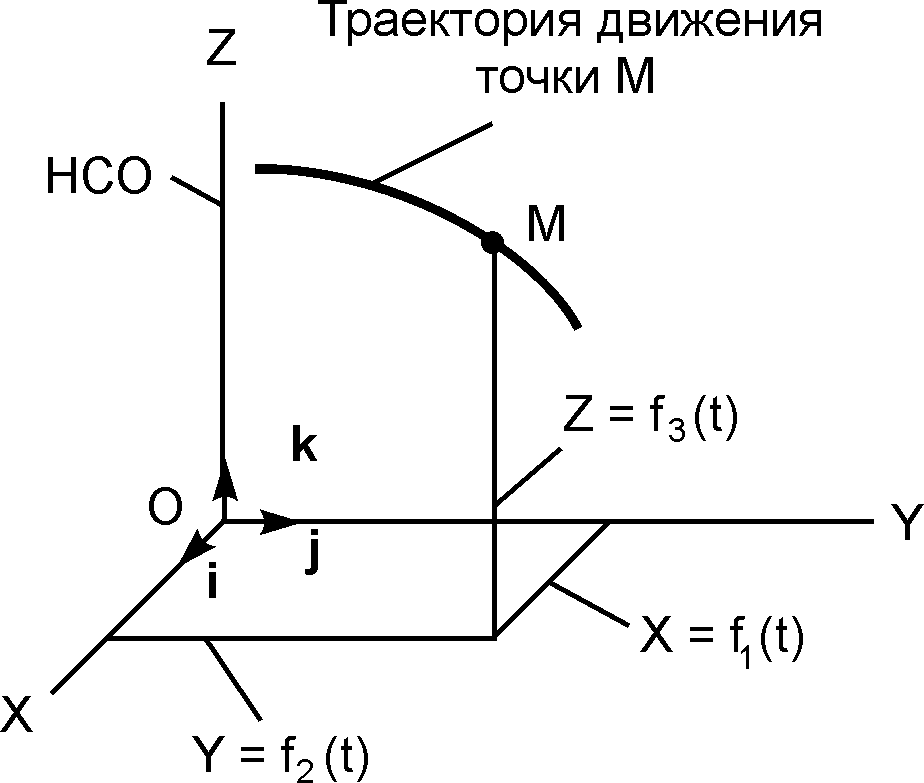

атыX, Y, Z движущейся точки М являются функциями времени t.

Систему трёх уравнений X = f₁(t); Y = f₂(t); Z = f₃(t) называют уравнениями движения точки в пространстве в декартовых координатах.

П

Рис. 2.2

ример: X = 10·t² + 1; Y = 7·t³ + t² + 1; Z = 10·sin(·t). Действительно, имея эти уравнения, можно для любого момента времени найти значения соответствующих координат X, Y, Z и по ним определить положение точки в пространстве в этот момент времени.

Движение точки М на плоскости (рис. 2.2) определяется двумя уравнениями: X = f₁(t); Y = f₂(t). Эти выражения называют уравнениями движения точки на плоскости в декартовой системе отсчёта.

Пример. Заданы уравнения движения точки в плоскости OXY. X = 3·t² + t² + t; Y = 7·cos(·t).

Уравнения движения, определяющие координаты точки в любой момент времени, рассматривают как параметрические уравнения траектории точки. При исключении параметра t из уравнений движения получают уравнение траектории точки в координатной форме (Y = f(t)).

П

Рис. 2.3

ример. Заданы уравнения: X = 4·t (см); Y = 16·t² – 1 (см) движения точки в плоскости OXY. Определить вид траектории движения точки, построить её график и найти положение точки на траектории движения в момент времени t₁ = 0,5 с.

Решение. Из уравнения X = 4·t находим t = X/4. Значение времени t подставляем в уравнение Y = 16·t² – 1. Получаем

Y = 16·(X/4)² – 1 = X² – 1.

Выражение Y = X² – 1 есть уравнение параболы (y= a·x²+b·x+c) с вершиной в точке с координатами (0, – 1). В момент времени t₁ = 0,5 с определяем координаты:

X(t₁) = 4·t₁ = 4·0,5 = 2 см > 0;

Y(t₁) = 16·(t₁)² – 1 = 16·(0,5)² – 1 = 3 см >0.

Показываем положение точки на траектории её движения (рис. 2.3).

Пример. Дано: X = 3·sin(·t), см (1); Y = 3·cos(·t), см (2); t₁ = 0,25 c. Определить вид траектории движения точки и её положение на траектории движения в момент времени t₁.

Решение. Уравнения движения точки представим в следующем виде: (X)² = (3·sin(·t))² (1^I); (Y)² = (3·cos(·t))² (2^I). Для решения используем тригонометрическую формулу sin²(α) + cos²(α) = 1.

Складывая левые и правые части уравнений (1^I) и (2^I), получим (X)² + (Y)² = 3²·(sin²(·t) + cos²(·t)) = 3²·1 или (X)² + (Y)² = 3². Известно, что уравнение (X)² + (Y)² = R² есть уравнение окружности радиусом R с центром в начале координат. Таким образом, точка д

Рис. 2.4

вижется по окружности радиусомR = 3 см (рис. 2.4).

Определяем положение точки на траектории движения в момент времени t₁.

X(t₁) = 3·sin(·t₁) = 3·sin(·0,25) = 3·0,707 = 2,121 см > 0.

Y(t₁) = 3·cos(·t₁) = 3·cos(·0,25) = 3·0,707 = 2,121 см > 0.

Показываем точку на траектории её движения (см. рис. 2.4).

ВНИМАНИЕ! Если точка не попадает на траекторию её движения, то:

1) неверно определен вид траектории движения;

2) неверно рассчитаны значения координат X(t₁), Y(t₁).

Прямолинейное движение точки М определяется одним уравнением движения X = f(t).

Пример. Дано: X = 10·t² + sin(2··t) + 3, см (рис. 2.5).

Рис. 2.5

Определить положение точки на траектории движения в начальный момент времени t₀ = 0 и в момент времени t₁ = 1 c.

Решение.

X(t₀) = 10·(t₀)² + sin(2··t₀) + 3 = 10·0² + sin(2··0) + 3 = 3 см > 0.

X(t₁) = 10·(t₁)² + sin(2··t₁) + 3 = 10·1² + sin(2··1) + 3 = 13 см > 0.

Значения координат X(t₀), X(t₁) наносим на рис. 2.5.