2.3. Скорость точки

Скорость – векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчёта.

Скорость точки всегда направлена по касательной к траектории её движения.

П

Рис. 2.6

усть заданы уравнения движения точки в пространстве:X = f₁(t); Y = f₂(t); Z = f₃(t) (рис. 2.6).

Разложим вектор V скорости точки на составляющие по координатным осям: V = V_OX + V_OY + V_OZ. Векторы V_OX, V_OY, V_OZ называют компонентами скорости по координатным осям. Вектор V скорости можно выразить векторным равенством:

V = i· + j· + k·,

где , , – проекции скорости V на соответствующие координатные оси.

В инженерных расчётах рекомендуется использовать следующие обозначения проекций скорости V на координатные оси: ; ; .

Сравнивая последние формулы, запишем равенство

V = V_OX + V_OY + V_OZ = i· + j· + k·.

Из этого равенства имеем:

V_OX = i·; V_OY = j·; V_OZ = k·.

Проекции скорости на координатные оси системы отсчёта равны первым производным по времени от соответствующих уравнений движения:

= dX/dt; = dY/dt;= dZ/dt,

где точка (·) означает символ однократного дифференцирования функции по времени.

Зная проекции скорости на координатные оси, находят модуль скорости по формуле

.

Ориентацию вектора скорости V в системе отсчёта OXYZ определяют по направляющим косинусам:

cos(V, i) = / V; cos(V, j) = / V; cos(V, k) = / V.

Д

Рис. 2.7

вижение точки в плоскостиOXY (рис. 2.7) задаётся двумя уравнениями движения: X = f₁(t); Y = f₂(t).

Модуль и направление скорости точки в этом случае определяются по формулам:

;

cos(V, i) = / V; cos(V, j) = / V.

П

Рис. 2.8

рямолинейное движение точки (рис. 2.8) задаётся одним уравнениемX = f(t).

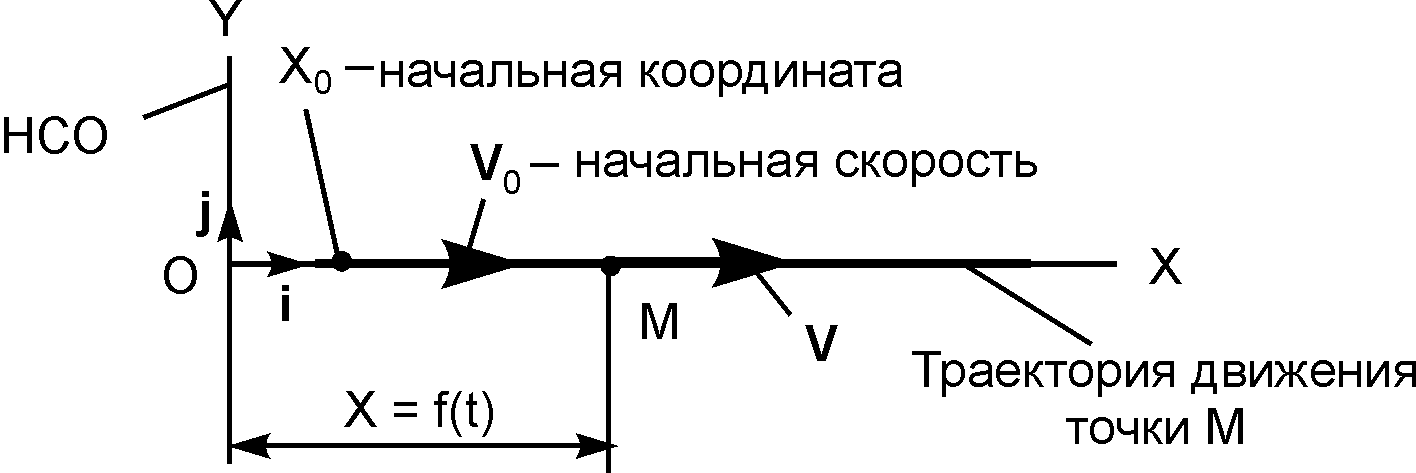
В этом случае модуль скорости точки равен абсолютной величине проекции скорости на координатную ось ОХ.

V = || = |dX/dt|.

При > 0 точка движется в сторону увеличения координаты Х, при < 0 – противоположно направлению оси.

2.4. Ускорение точки

Ускорение – векторная величина, характеризующая быстроту изменения величины и направления скорости.

Ускорение всегда направлено в сторону вогнутости траектории движения.

Рассматривается движение точки на плоскости в системе отсчёта OXY (рис. 2.9) по заданным уравнениям движения X = f₁(t); Y = f₂(t).

Согласно рис. 2.9 запишем векторное равенство

а = а_ОХ + a_OY = i· + j·,

где а – ускорение точки; а_ОХ, a_OY компоненты ускорения по координатным осям; , – проекции ускорения на координатные оси.

Здесь две точки (··) означает символ двойного дифференцирования функции по времени.

Рис. 2.9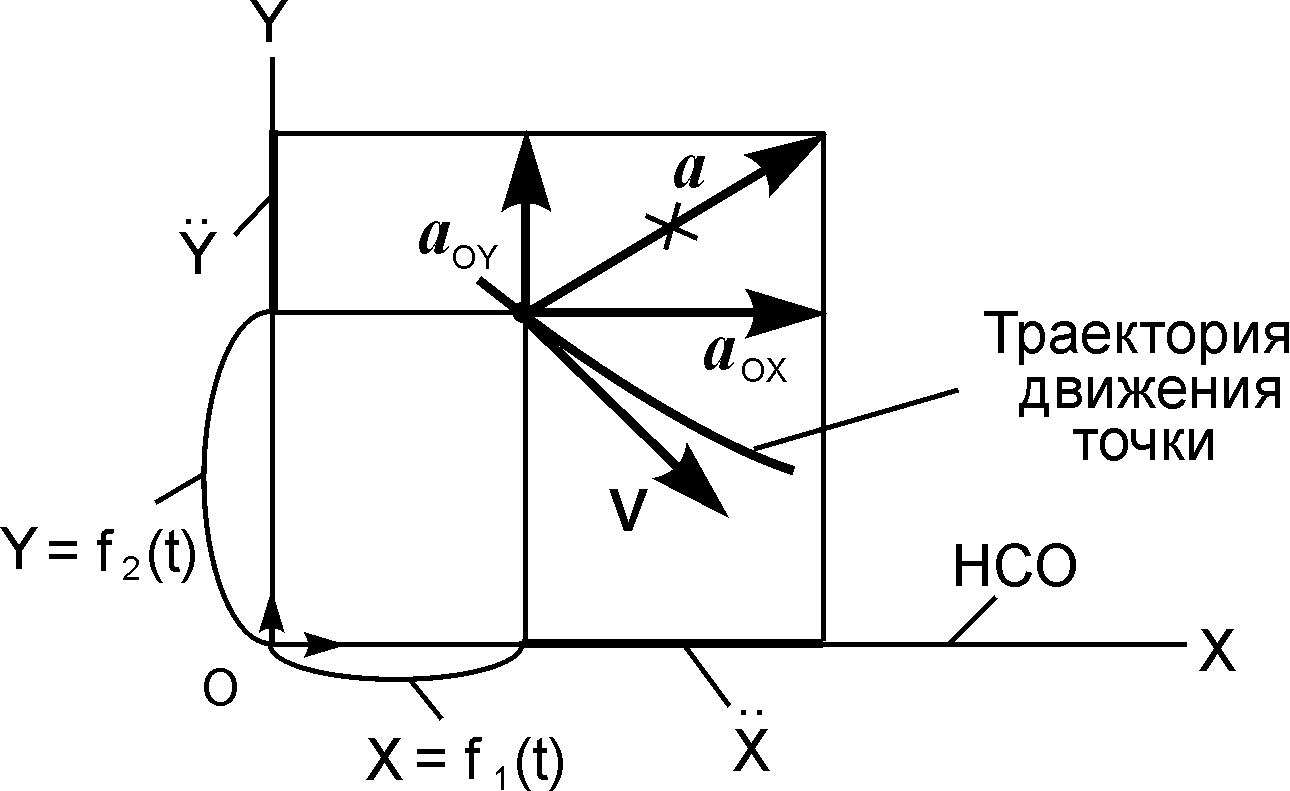

Распространяя полученный результат на пространство (система отсчёта OXYZ), получим

а = а_ОХ + a_OY + a_OZ = i·+ j·+ j·.

Как правило, проекции ускорения а на координатные оси в технической литературе обозначаются так: , , .

Проекции ускорения точки на координатные оси равны вторым производным по времени от соответствующих уравнений движения или первым производным по времени от проекций скорости на соответствующие оси.

= d₂X/dt² = ;

= d₂Y/dt² = ;

= d₂Z/dt² = .

Модуль ускорения находится по следующим формулам:

a = (точка движется в пространстве);

a = (точка движется в плоскости);

a = || (точка движется по прямой линии).

Направляющие косинусы находятся по следующим формулам:

cos(a, i) =/ a;cos(a, j) = / a;cos(a, k) = / a.

Зная направляющие косинусы, вектор ускорения а ориентируют в пространстве.

Рассматривается движение точки по прямой линии согласно заданному уравнению движения X = f(t) (рис. 2.10).

Рис. 2.10

При таком движении справедливо равенство а = а_ОХ = i·. На рис. 2.10 дополнительно показано ускорение а₀ – начальное ускорение точки при t₀ = 0.

Примечания:

1. Если проекции ускорения на координатные оси положительны (> 0, > 0, > 0), то компоненты ускорения по координатным осям (а_ОХ, a_OY, a_OZ) направлены в те же стороны, что и единичные векторы (I, j, k) системы отсчёта OXYZ.

2. Если проекции ускорения на координатные оси отрицательны (< 0, < 0, < 0), то компоненты ускорения по координатным осям (а_ОХ, a_OY, a_OZ) направлены в стороны, противоположные ортам (I, j, k) системы отсчёта OXYZ.

Рассмотрим более подробно движение точки на координатной оси ОХ (рис. 2.10) по заданному уравнению движения X = f(t).

Если проекция скорости V и проекция ускорения а точки совпадают по знаку, то точка движется ускоренно. При > 0 и>0 точка движется в сторону увеличения координаты Х ускоренно. Если< 0 и< 0, то точка движется в сторону уменьшения координаты Х ускоренно. Если> 0 и< 0, то точка движется в сторону увеличения координаты замедленно. Если< 0 и> 0, то точка движется в сторону уменьшения координаты Х замедленно.

Если проекция ускорения на ось ОХ постоянна (=const), то такое движение называют равнопеременным. При условии, что =const ≠ 0, уравнение равнопеременного движения точки записывают в виде

X = X₀ + ₀·t + (·t²)/2,

где X₀ – значение координаты точки в начальный момент времени; ₀ - проекция начальной скорости V₀ на координатную ось ОХ в начальный момент времени.

Если =const > 0, то такое движение называют равноускоренным.

Если =const < 0, то движение точки называют равнозамедленным.

Если = 0, то такое движение называютравномерным. Уравнение равномерного движения имеет вид X = X₀ + ·t.

При условии, что = f(t) ≠ const, для получения уравнения движения выражение = f(t) необходимо дважды проинтегрировать.

Пусть, например, = 2·t. Представим это выражение в виде d/dt = 2·t. Разделим переменные в этом дифференциальном уравнении d= 2·t·dt. Первый интеграл от этого выражения имеет вид = 2·(t²/2) + C₁ = t² + C₁, где С₁ – постоянная интегрирования, которую находят по начальным условиям движения. Пусть при t₀ = 0 проекция начальной скорости V₀ на ось ОХ не равна нулю: ₀ ≠ 0. Тогда при t₀ имеем ₀ = (t₀)² + C₁. Откуда С₁ = ₀. Внося значение постоянной С₁ в выражение, полученное при первом интегрировании, имеем =t² + ₀. Так как =dX/dt, то после разделения переменных имеем следующее дифференциальное уравнение движения dX = t²·dt + ₀·dt. Интегрируя это уравнение, получим X = t³/3 + ₀·t + C₂, где С₂ – постоянная интегрирования, определяемая по начальным условиям движения. Пусть при t₀ = 0 координата Х₀ ≠ 0. Тогда X₀ = (t₀)³/3 + ₀·t₀ + C₂ или С₂ = Х₀. Окончательно имеем уравнение прямолинейного движения

X = (t)³/3 + ₀·t + X_o.

Таким образом, если заданы уравнения движения точки в координатной форме, то можно в любой момент времени определить следующие кинематические характеристики:

1. траекторию движения;

2. положение точки на траектории движения;

3. проекции скорости на координатные оси, а, следовательно, и модуль скорости;

4. ориентацию вектора скорости в системе отсчёта по её направляющим косинусам;

5. проекции ускорения на координатные оси и модуль ускорения;

6. положение вектора ускорения в системе отсчёта по его направляющим косинусам.