§19. Колебания систем с несколькими степенями свободы

 Литература: [3] (§ 43), [8] (§ 23).

 Некоторые важные положения

 Малые свободные колебания консервативной системы с s степенями свободы анализируются аналогично тому, как это делается для одномерного осциллятора (§ 17).

 По аналогии с (17.2) и (17.3) вводятся кинематические параметры:

m_{i j} = m_{j i} = = (19.1)

и динамические параметры:

q = q₀ .

k_{i j} = k_{j i} = (19.2)

Индексы i и j = 1, 2, ..., s. Символ q = {q_j} обозначает совокупность обобщенных координат, q₀ – совокупность обобщенных координат в положении равновесия, которое соответствует минимуму потенциальной функции U(q). Переменные x = q – q₀ характеризуют отклонение от положения равновесия.

В качестве аналога (17.4) получается система s дифференциальных уравнений:

= 0 . (19.3)

Этой системе удовлетворяют функции

x_j = A_j exp(i  t) , (19.4)

где коэффициенты A_j находятся из следующей однородной системы линейных алгебраических уравнений:

A_j = 0 . (19.5)

Физический смысл обобщенных координат имеют, конечно, действительные части комплексных величин x_j.

Нетривиальные решения (A_j  0) система (19.5) имеет при условии, что ее детерминант равен нулю:

Det (k_{i j} – ² m_{i j}) = 0 . (19.6)

Равенство (19.6) представляет собой вековое уравнение для нахождения собственных частот системы ₀ = _ (индекс  = 1, 2, ..., s).

 Общее решение системы (19.3) – суперпозиция функций (19.4):

x_j = С_ exp(i _ t) = Q_ , (19.7)

где Q_ = С_ exp(i _ t). (19.8)

Соотношение (19.7) устанавливает взаимно однозначное соответствие наборов величин {x_j} и {Q_}. Это означает, что вместо обобщенных координат x_j рассматриваемую систему частиц можно описывать также обобщенными координатами Q_. Разумеется, здесь речь идет о действительных частях найденных комплексных функций.

 Обобщенные координаты Q_ многомерного осциллятора, изменяющиеся монохроматически (то есть по гармоническому закону (19.8) с определенной частотой _), называются нормальными координатами, а их изменения с течением времени – нормальными колебаниями.

Поскольку обобщенные координаты независимы, можно возбудить отдельно те или иные нормальные колебания.

 Функция Лагранжа в нормальных координатах принимает канонический вид:

L = , (19.9)

то есть представляет собой сумму лагранжианов независимых линейных гармонических осцилляторов, совершающих нормальные колебания с частотами, которые определяются по формулам

_ = . (19.10)

 Разъяснения и дополнения

 Малые колебания многомерного осциллятора называют гармоническими, так как они описываются линейной комбинацией (19.7) гармонических функций различных частот _. Нормальные колебания – монохроматические.

 Нахождение нормальных колебаний заключается в определении их частот _ и соответствующих им нормальных координат Q_.

Первый способ нахождения нормальных колебаний:

1) по формулам (19.1) и (19.2) вычисляются параметры m_{i j} и k_{i j} системы;

2) посредством решения векового уравнения (19.6) определяются собственные частоты _;

3) для каждой собственной частоты _ находятся коэффициенты А_j из системы (19.5);

4) после подстановки А_j в (19.7) нормальные координаты Q_ выражаются через исходные обобщенные координаты x_j решением этой системы уравнений.

Второй способ нахождения нормальных колебаний:

1) искусственным приемом функция Лагранжа приводится к каноническому виду (19.9);

2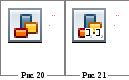)определяются нормальные координаты Q_ и параметры m_ и k_;

3) вычисляются собственные частоты по формулам (19.10).

Первый способ громоздкий, но зато универсальный. Для его реализации целесообразно использовать компьютер. Второй – быстро приводит к цели, если только лагранжиан легко приводится к каноническому виду.

 На рисунке 20 изображена система двух связанных маятников.

На рисунке 21 – та же система (вид сбоку) после отклонения от положения равновесия.

Изменение с течением времени углов ₁ и ₂ происходит, как показывает наблюдение, не по монохроматическому закону, о чем свидетельствует то обстоятельство, что амплитуда колебаний одного маятника постепенно убывает до нуля, после чего снова возрастает, а другого – наоборот.

Можно возбудить по отдельности два нормальных колебания, соответствующих обобщенным координатам Q₁ = ₁ + ₂ и Q₂ = ₁ – ₂.

Первое соответствует синхронному движению маятников, находящихся все время в одинаковых фазах (Q₂ = 0  ₁ = ₂). Второе – движению в противофазах (Q₁ = 0  ₁ = – ₂).

? Задания и контрольные вопросы

1. В чем сходство многомерного и одномерного осцилляторов и чем они отличаются друг от друга?

2*. Получите уравнения (19.3) и (19.5).

3. Расскажите о вековом уравнении и собственных частотах.

4. Расскажите о нормальных координатах и нормальных колебаниях.

5. Что дает право рассматривать многомерный осциллятор как совокупность нескольких независимых одномерных осцилляторов?

6*. Проведите компьютерный анализ многомерного осциллятора первым способом на примере связанных маятников 43.2 [3]. Воспользуйтесь для этого файлом «Изучение М.О.».

7*. Расскажите об анализе многомерного осциллятора преобразованием лагранжиана к каноническому виду.