IV. Движение в центральном поле §14. Задача двух тел

 Литература: [8] (§ 13).

 Разъяснения и дополнения

Рассматривается система двух частиц, изображенная на рис. 12. Массы частиц – m₁ и m₂; потенциальная энергия U зависит от расстояния r = ₁₂  между ними: U = U(r).

Система двух частиц замкнута. Поэтому ее импульс сохраняется: = const. Задача упрощается, если положить= (m₁ + m₂) _C = 0, иначе говоря, если перейти в систему центра масс. В новой системе отсчета положение центра масс С остается неизменным (_C = 0  _C = const). Потребуем далее, чтобы_C = 0, то есть совместим начало отсчета с центром масс. Придем к более простой ситуации, изображенной на рис. 13. Для нее имеют место следующие равенства:

= ₂ – ₁ , (14.1)

₁ = – , (14.2)

₂ = . (14.3)

 Функцию Лагранжа рассматриваемой системы, благодаря соотношениям (14.1) – (14.3), можно привести к виду

L =  ² – U(r), (14.4)

где  = , или=+. (14.5)

Величину  называют приведенной массой.

В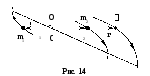ыражение (14.4) означает, чтозадача двух тел сводится к задаче о движении одной частицы ( -точки). Масса -точки равна приведенной массе частиц (14.5). Радиус-вектор характеризует положение второй частицы относительно первой (см. (14.1) и рис. 13). Начало отсчета – центр масс. Потенциальная функция U зависит только от расстояния r до этого центра. Поле, описываемое такой потенциальной функцией, называют центральным.

 Если задача о движении -точки в центральном поле решена (найдено уравнение = (t)), то формулы (14.2) и (14.3) позволяют описать движение каждой частицы.

На рисунке 14 показаны траектории и направления движения -точки и частиц m₁ и m₂. Траектории движения этих частиц и -точки подобны.

? Задания и контрольные вопросы

1*. Приведите примеры конкретных систем, которые описывает задача двух тел.

2. Почему задачу двух тел целесообразно решать в системе центра масс?

3*. Выведите формулы (14.2) и (14.3).

4*. Получите соотношение(14.4).

5. Что такое -точка?

6. Какое поле называют центральным? Приведите примеры центральных полей.

7*. Расскажите, как определяется движение каждой частицы, если известно движение -точки.

§15. Общие закономерности движения частицы в центральном поле

 Литература: [8] (§ 14).

 Некоторые важные положения

 При решении задачи о движении частицы в центральном поле используются полярные координаты r и . Функция Лагранжа в этих координатах имеет вид:

L =  (² + r^{2 2}) – U(r) . (15.1)

 Момент импульса L_Z относительно оси Z, проходящей через центр и коллинеарной вектору , остается постоянным. Он выражается равенством:

L_Z = =  r² = const, (15.2)

в котором L – функция Лагранжа (не путайте с модулем момента импульса ).

Из-за равенства L_Z = const неизменной оказывается и секторная скорость:

= = const , (15.3)

где d = r² d / 2.

Утверждение о постоянстве секторной скорости планеты при ее движении вокруг Солнца получило название второго закона Кеплера.

 Сохранение энергии E частицы приводит к уравнению:

=  , (15.4)

где U_ЭФ = U(r) + U_ЦБ , (15.5)

U_ЦБ =. (15.6)

Величина E включает в себя, помимо кинетической энергии, еще и потенциальную энергию частицы в центральном поле.

 Равенства (15.2) и (15.4) в неявном виде содержат кинематические уравнения движения. Исключая время из этих равенств, получим дифференциальное уравнение траектории:

=  . (15.7)

 Разъяснения и дополнения

 Речь идет, вообще говоря, о движении -точки. Однако если массы двух тел сильно различаются (m₁ >> m₂), то из (14.5) и (14.3) следует, что движение -точки мало отличается от движения частицы меньшей массы относительно другого тела. Поэтому, говоря о движении частицы в центральном поле, можно иметь в виду, например, движение космического корабля с выключенным двигателем относительно Земли или движение -частицы относительно тяжелого атомного ядра.

 Сила, действующая на частицу в центральном поле, коллинеарна радиус-вектору частицы (↑↨).

Это становится понятным, если вспомнить, что = –U. Перпендикулярные к вектору составляющие градиента в сферической системе координат пропорциональны величинам и . Обе эти производные в центральном поле равны нулю.

Вследствие соотношения ↑↨ в центральном поле сохраняется момент импульса :

= = [] = 0  = const. (15.8)

 Сохранение момента импульса означает, что частица в центральном поле движется по траектории, которая лежит в плоскости, перпендикулярной и проходящей через центр поля.

Действительно, = [] =  []. Отсюда следует, что в любой момент времени  и  , то есть плоскость, образованная вектором и бесконечно малым отрезком dt траектории, остается перпендикулярной неизменному вектору .

 Формула (15.4) аналогична (13.1). Это позволяет проводить анализ движения подобно тому, как это делалось в § 13.

Н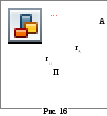а рисунке 15 изображен график эффективной потенциальной энергии (15.5) при некоторых ограничениях на функцию U(r). Предполагается, что, во-первых, U(r) < 0 (притягивающий центр), во-вторых, при r  величина U(r)  0, а при r  0 U(r) << U_ЦБ (15.6).

Энергия E рассматриваемой системы сохраняется, поскольку исходная система двух частиц замкнута и консервативна.

Можно отнести величину E и непосредственно к -точке. Тогда энергия -точки представляет собой сумму ее кинетической энергии и «потенциальной энергии в поле». Придерживаясь школьной терминологии, следовало бы говорить об энергии системы «-точка – поле».

Прямая E = const на рисунке 15 пересекает график в точках П и А, определяющих минимальное (r_П) и максимальное (r_А) расстояния частицы от центра.

В области пространства r_П  r  r_А происходит финитное движение. Эта область на плоскости движения ограничена окружностями с радиусами r_П и r_А соответственно (рис.16). Траектория движения представляет собой, вообще говоря, незамкнутую розетку, часть которой изображена на рисунке 16.

Точки А, наиболее удаленные от центра О, называют апоцентрами, а точки П, наименее удаленные от центра, перицентрами. Про эти точки траектории, а также соответствующие им точки А и П на рисунке 15 говорят, что они являются точками поворота. В них, в соответствии с формулами (15.7) и (15.2), = 0, но 0, то есть происходит поворот радиус-вектора при неизменном его модуле.

Из-за двух знаков перед корнем в формуле (15.7) траектория симметрична относительно линий ОА и ОП – линий абсид.

? Задания и контрольные вопросы

1. Приведите примеры систем, описываемых задачей о движении частицы в центральном поле.

2. К существованию какого интеграла движения приводит центральная симметрия поля и почему?

3*. Объясните, как получаются формулы (15.1) и (15.2).

4. Какие следствия для частицы в центральном поле имеют место в силу того обстоятельства, что сохраняется момент импульса?

5. Расскажите о втором законе Кеплера.

6*. Выведите уравнения, определяющие функции  =  (t) и r = r(t) для частицы в центральном поле.

7. При каких условиях возможны финитные движения частицы в центральном поле?

8. Расскажите о траекториях финитного движения частицы в центральном поле.

9. Расскажите о перицентрах и апоцентрах.

10*. Расскажите о проблеме падения частицы на притягивающий центр.