Вопросы для самоконтроля

1. Биномиальный закон распределения случайной величин.

2. Закон распределения Пуассона.

3. Равномерный закон распределения.

4. Показательный закон распределения.

5. Нормальный закон распределения.

Ответы на тестовые задания

Номер теста	4.1	4.2	4.3	4.4	4.5	4.6	4.7	4.8	4.9	4.10
Правильный ответ	1	3	1	2	2	2	2	1	1	5

Номер теста	4.11	4.12	4.13	4.14	4.15	4.16	4.17	4.18	4.19	4.20
Правильный ответ	5	4	2	1	5	1	3	3	2	2

Номер теста	4.21	4.22	4.23	4.24	4.25	4.26
Правильный ответ	1	1	3	4	5	2

5. Двумерные случайные величины

Двумерной случайной величинойназывается случайная величина (X;Y), задаваемая рядом распределения с двумя входами

y x	y1	…	ym
x1	p11	…	p1m
…	…	…	…
xn	pn1	…	pnm

Так как события {x=x_i;y=y_j} образуют полную группу, то.

Пример 5.1.Двумерная случайная величина задана рядом распределения.

y x	y1 = 1	y2 = 2
x1= 0	0,1	0,4
x2= 3	0,2	p(x2; y2)

Какова вероятность p(x₂;y₂)?

Решение

p(x₂;y₂) = 1 – (0,1 + 0,4 + 0,2) = 0,3.

_{Ответ: 0,3.}

Тест 5.1.Двумерная случайная величина задана рядом распределения

x	y1 = 1	y2 = 2
x1= 0	0,1	0,4
x2 = 3	0,2	p(x2;y2)

Вероятность p(x₂;y₂) равна:

1) 0;

2) 0,3;

3) 0,2;

4) 0,1;

5) 0,4.

Пример 5.2.Двумерная случайная величина задана рядом распределения

x y	y1 = 1	y2 = 2
x1 = 0	0,1	0,4
x2 = 3	0,2	0,3

Записать ряд распределения случайной величины X.

Решение

X	0	3
pi	0,1 + 0,4	0,2 + 0,3

Тест 5.2. Двумерная дискретная величина (X, Y) задана законом распределения

	1	2
0	0,1	0,3
1	0,4	p(x2; y2)

Вероятность p(x₂; y₂) равна:

1) 1;

2) 0,7;

3) 0,6;

4) 0,2;

5) 0.

Тест 5.3.Двумерная случайная величина задана рядом распределения

	y1 = 1	y2 = 2
x1 = 0	0,1	0,4
x2 = 3	0,2	0,3

Вероятность появления x₂ = 3 равна:

1) 0;

2) 0,1;

3) 0,2;

4) 0,3;

5) 0,5.

Тест 5.4.Двумерная случайная величина задана рядом распределения

	y1= 1	y2= 2
x1= 0	0,1	0,4
x2= 3	0,2	0,3

Вероятность появления у₁ = 1 равна:

1) 0;

2) 0,1;

3) 0,2;

4) 0,3;

5) 0,5.

Зависимость между случайными величинами x иy описываеткорреляционный момент:

.

Коэффициентом корреляции случайных величинX и Y, между которыми предполагается линейная корреляционная связь, называется величина, определяемая по формуле

.

Корреляционной матрицей называется матрица вида

.

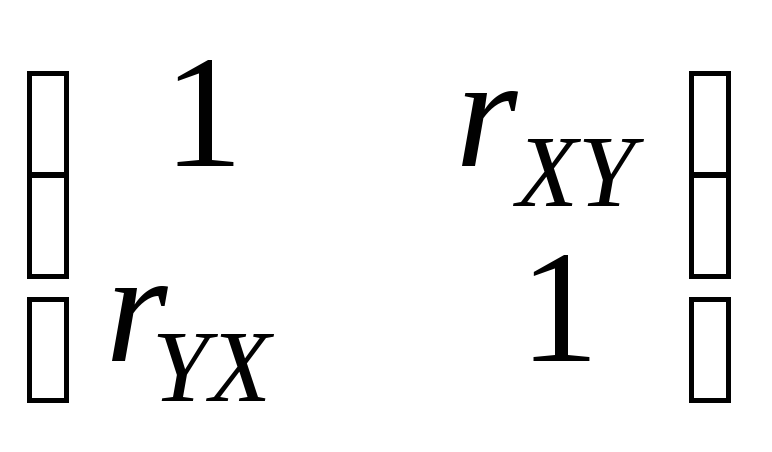Корреляционная матрица также устанавливает взаимосвязь наборов выборочных данных по величине:

• при 0 < r_XY < 1 большим значениям случайной величины X соответствуют большие значения случайной величины Y;

• при –1 < r_XY < 0 большим значениям случайной величины X соответствуют меньшие значения случайной величины Y (или наоборот);

• при r_X = 0 данные двух случайных величин некоррелированы;

• при существует линейная функциональная зависимость между случайными величинамиX и Y.

Пример 5.3. Корреляционный момент k_xy = 270. Какова зависимость между X и Y?

Решение

Так как k_xy имеет размерность, то можно говорить лишь о прямой зависимости междуХиY.

Пример 5.4. Коэффициент корреляцииr_XY = – 0,375. Какова зависимость между ХиY?

Решение

По коэффициенту можно судить о виде зависимости и ее силе. Так как r_XY = – 0,375 < 0, то зависимость обратная, так как, то связь междуХиY высокая.

Тест 5.5. Известно, чтоk_xy= 2,75,_Х= 3,1,_Y= 2,5. Коэффициент корреляции равен:

1) ;

2) ;

3) .

Тест 5.6. Коэффициент корреляцииr_XY = 0. Тогда зависимость междуXиY:

1. прямая линейная;

2. обратная линейная;

3. данные двух случайных величин некоррелированы.

Тест 5.7. Коэффициент корреляцииr_XY = 1. Тогда зависимость между XиY:

1. прямая линейная;

2. обратная линейная;

3. данные двух случайных величин некоррелированы;

4. функциональная прямая линейная.

Тест 5.8. Коэффициент корреляцииr_XY = –1. Тогда зависимость междуXиY:

1. прямая линейная;

2. обратная линейная;

3. данные двух случайных величин некоррелированы;

4. функциональная обратная линейная.