Нормальное ускорение точки С во вращении коромысла 3 вокруг неподвижной оси шарнира D

aCDn =ω32lDC = 0

(ибо угловая скорость мгновенно-неподвижного коромысла ω3 = 0 ) – точка n3

перпендикулярную прямой DC, – направление касательного ускорения aτDC .

Проведенные прямые пересекаются в точке с. Точки s2 и s3 делят длины (bc) и (dc) пополам. Отрезки (πs2) и (πs3) изображают ускорения центров масс S2 и S3.

Угловое ускорение шатуна 2

Нетрудно заметить, что ускорения точек мгновенно-неподвижного коромысла 3, изображенные отрезками (πс) и (πs3), в отличие от скоростей не равны нулю.

Лекция 5. Силовой анализ механизма

5.1 Силовой анализ группы Ассура

На рисунке 5.1 изображена группа Ассура 2-3, составленная кулисой 3 и кулисным камнем 2 кулисного механизма на рисунке 4.1. К ним приложены силы инерции

ускорение (4.9). Направления сил инерции и инерционного момента (рис. 5.1) противоположны ускорениям.

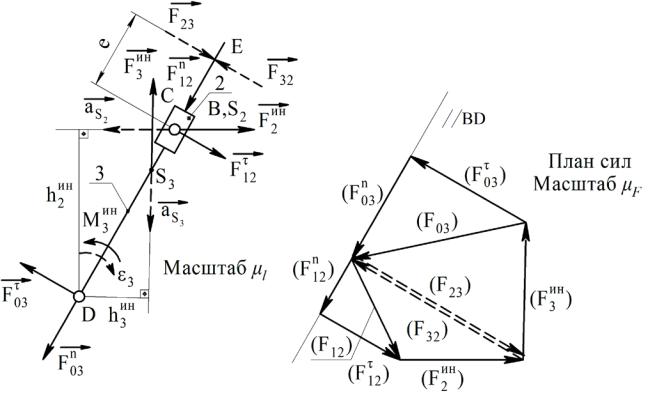
Рассмотрим инерционную нагрузку группы вместе с реакциями F12 и F03 кривошипа 1 и стойки 0. Их направления неизвестны – представляем их

составляющими F12n , F03n , направленными вдоль прямой BD, и F12τ , F03τ , направленными перпендикулярно линии BD. Реакция кулисного камня F23 и реакция кулисы F32 равны по величине и противоположны по направлению и в

случае поступательной пары С перпендикулярны направляющей – прямой DB, однако точка их приложения неизвестна.

Инерционная нагрузка группы «уравновешивается» реакциями в кинематических парах B и D; инерционная нагрузка любого из звеньев группы

30

«уравновешивается» реакциями во внешней и внутренней кинематических парах, в которые входит звено.

Рассмотрим «равновесие» группы в целом (рис. 5.1). Из уравнения моментов

∑mD = −F12τ (DB)µl − F2ин h2инµl + F3ин h3инµl + M3ин = 0

находим составляющую реакции кривошипа F12τ H.

Рисунок 5.1 – Группа 2-3 и ее план сил

В дальнейшем рассматриваем «равновесие» кулисного камня: на него действуют найденная реакция кривошипа F12τ ; заданная сила инерции F2ин ;

неизвестная реакция кулисы F32 , перпендикулярная линии BD, и неизвестная составляющая F12n реакции кривошипа, направленная вдоль прямой BD.

найдем, строя план сил в масштабе µF = F12τ / (F12τ )Н/мм, (F12τ )мм – отрезок, изображающий силу F12τ . Начиная из произвольной точки направления, параллельного прямой BD (и реакции F12n ), проводим отрезок (F12τ )мм,

изображающий силу F12τ , из его конца – отрезок (F2ин )= F2ин / µF мм, из конца отрезка (F2ин ) проводим прямую, параллельную реакции F32 , то есть прямую,

перпендикулярную линии BD, до пересечения с направлением, параллельным прямой BD (и силе F12n ). Многоугольник уравновешенных сил должен (рис. 5.1)

31

замыкаться, искомые реакции F32 и F12n тем самым определены. Реакция кривошипа

пересечения с направлением, параллельным реакции F03n , проведенным из начала вектора (F23 ). Построенный многоугольник сил должен замыкаться, тем самым

неизвестные реакции определены. Реакция стойки

F03 = F03τ + F03n

изображается отрезком (F03 ).

Остается найти расстояние e до точки приложения реакций F23 = −F32 .

Беря уравновешенные силы, действующие на кулисный камень 2, составим уравнение моментов относительно точки B:

2

∑mB = F12τ 0 + F12n 0 + F2ин 0 + F32 e = 0,

откуда расстояние e = 0: реакции F23 , F32 , приложены в точке B (как и все другие силы, действующие на камень 2).

32

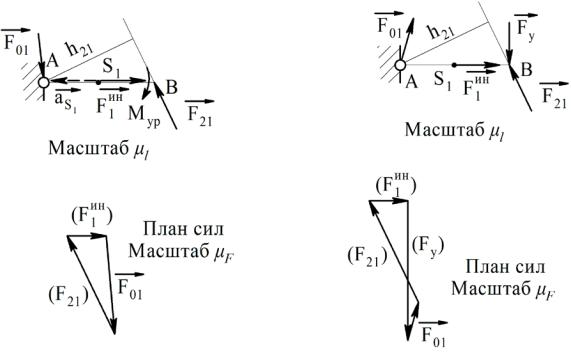
– забыта реакция двигателя [2, с. 273-274], сводящаяся к уравновешивающей силе Fу с заданной линией действия или уравновешивающему моменту Mу. В первом

случае вал двигателя может соединяться с главным валом кривошипа 1 посредством зубчатой передачи, во втором случае – муфтой.

На рисунке 5.2 показан случай реактивного (уравновешивающего) момента. Добавляя его к сумме (5.2), найдем:

кулисного камня 2, равную по модулю реакции (5.1). Прочие силы изображаются отрезками (F1ин )= F1ин / µF , (F01 ). Многоугольник сил F21 + F1ин + F01 = 0 замкнут, отрезок (F01 ), изображающий реакцию стойки, тем самым определен.

На рисунке 5.3 показан случай реактивной (уравновешивающей) силы, перпендикулярной кривошипу. Добавляя к сумме (5.2) момент уравновешивающей силы

mA (Fу )= −Fу l1 Н∙м,

найдем:

33