π = const, β = const, δ = const.

Рисунок 13.2 – Деформация фрагмента бруса

13.2 Гипотеза о ненадавливании продольных волокон

На боковых, верхней и нижней гранях фрагмента (рис. 13.2) нагрузок (и напряжений) нет. Если же на поверхности бруса действуют распределенные по ней силы, давления на продольные волокна намного меньше напряжений σ на их торцах (см. точные решения теории упругости) – давлениями продольных волокон друг на друга можно пренебречь. Гипотеза: продольные волокна не давят друг на друга, напряжений, показанных на рисунке 13.3 штриховыми стрелками, нет.

Рисунок 13.3 – Продольные волокна не давят друг на друга

Напряженное состояние продольного волокна (рис. 13.3) – линейное.

13.3 Закон Гука

Полагая в дальнейшем, что деформация нагруженного бруса упругая (исчезающая при разгрузке) – относительное удлинение продольного волокна

(13.1)

86

где E – характеристика жесткости материала бруса, называемая модулем Юнга, или модулем продольной упругости.

13.4 Распределение нормальных напряжений в поперечном сечении

бруса

Геометрические характеристики в формулах (13.4):

A = ∫dA

A

– площадь сечения;

Sy = ∫xdA, Sx = ∫ydA

AA

–статические моменты площади сечения, равные нулю, если оси x и y –

центральные;

Ix = ∫y2dA, Iy = ∫x2dA

AA

–осевые моменты инерции площади сечения, максимальный и минимальный,

если оси x и y – главные;

Ixy = ∫xydA

A

– центробежный момент инерции площади сечения, равный нулю, если оси x и y – главные.

На рисунке 13.2 оси координат – естественные, то есть центральные главные, следовательно, характеристики

Sx = 0, Sy = 0 , Ixy = 0.

Уравнения (13.4) приобретают вид

N = DA ,

−M x = BIx ,

−M y = PIy ,

87

выражаются через внешние силы – см. выражения (12.8, 12.10) – линейно, соответственно, и напряжения (13.5) выразятся через внешние силы линейно. Следовательно, внутренние силовые факторы (здесь M x , M y и N) и напряжения

(13.5) от группы сил равны алгебраическим суммам внутренних силовых факторов и напряжений от каждой из этих сил в отдельности.

13.6 Простые и сложные деформации бруса

В частном случае зависимости (13.5) напряжения от группы внутренних силовых факторов равны суммам напряжений от каждого из них в отдельности. В этих последних случаях (когда действует только один внутренний силовой фактор) говорят о простых деформациях бруса – растяжении (сжатии) и прямом изгибе. При наличии нескольких внутренних силовых факторов говорят о сложной деформации бруса, или о сложном сопротивлении. Если факторы M x ≠ 0, M y ≠ 0 , N = 0 , сложная деформация бруса представляется суммой двух

прямых изгибов в главных плоскостях инерции бруса xz , yz . Именно таков изгиб

вала в лекции 12. Если все силы, действующие на брус, находятся в одной плоскости, не совпадающей ни с одной из главных плоскостей, изгиб (рис. 13.4) называется косым. Все три фактора в формуле (13.5) действуют при внецентренном растяжении (сжатии) (рис. 13.5). Приведем силу F – равнодействующую внутренних сил к центру тяжести сечения С – началу естественных осей координат x, y:

N = F ,

M x = −FyF ,

M y = −FxF .

Изгибающие моменты здесь отрицательные, так как первая координатная четверть сечения (первый квадрант) растягивается. Положительные изгибающие моменты отвечают сжатию первого квадранта.

88

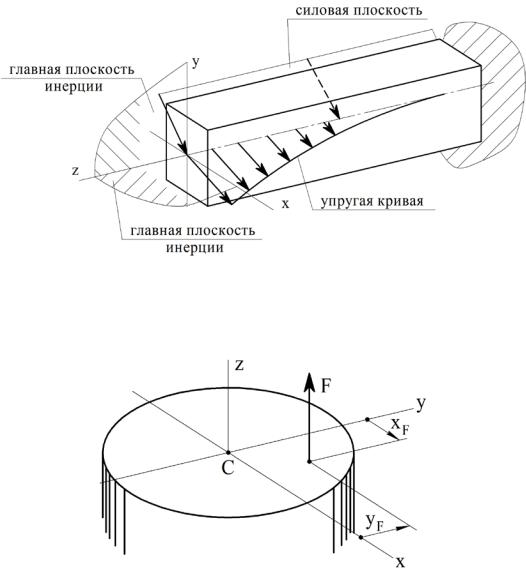
Рисунок 13.4 – Косой изгиб: плоскость искривленной продольной

оси (плоскость прогибов) не совпадает с силовой плоскостью

Рисунок 13.5 – Внецентренное растяжение

13.7 Условие прочности при растяжении (сжатии)

При растяжении (сжатии) действует один внутренний силовой фактор – продольная сила N , положительная при растяжении и отрицательная при сжатии. Такая деформация бруса возникает, когда внешние силы, действующие по одну сторону от поперечного сечения, приводятся к равнодействующей F с линией действия – продольной осью бруса. Нормальные напряжения (рис. 13.6)

практике условие (13.6) усиливают, вводя требуемый «коэффициент безопасности» [s]:

89