Правило знаков для моментов в уравнениях равновесия (16.2): момент силы, "вращающей" вал вокруг взятой оси против хода часовой стрелки (при наблюдении с конца оси), считаем положительным. Например, силы Fм и Ft
"вращают" вал вокруг оси By против хода часовой стрелки – моменты обеих сил в первом уравнении (16.2) положительные; реакция RDx "вращает" вал вокруг оси By по ходу часовой стрелки – ее момент в первом уравнении (16.2) отрицательный.
16.3 Изгибающие моменты
При изгибе в вертикальной плоскости (рис. 16.2) искривляется участок BD , консоль AB поворачивается, не искривляясь. На искривленном участке BD сжатыми оказываются верхние "волокна", в пределах всего участка BD изгибающие моменты Мх считаем положительными.
Изгибающий момент в произвольном сечении Е участка BС найдем, приводя единственную "левую" силу RBу к сечению Е, то есть перенося силу RBу
в сечение Е и добавляя к ней пару сил с моментом (изгибающим моментом) RBуz. Свяжем теперь положительный знак момента с направлением силы RBу :
изгибающий момент вертикальной силы, направленный вверх, положительный. Итак, в пределах участка ВС изгибающий момент
Мх = RBуz,
изменяясь по линейному закону, изменяется от нуля в сечении B (при z = 0 ) до наибольшего RBуl1 в сечении C (при z =l1 ).
В пределах участка DC удобнее пользоваться "правой" силой RDу . Положительный знак ее момента отвечает направлению силы RDу (направлена вверх). В сечении D , очевидно, M x = 0 , наибольший момент на участке DE возникает в наиболее удаленном от силы RDу сечении C :
M x = RDуl1.
Если учесть решение уравнения равновесия (16.1), найдем в сечении C
M x = RDуl1 = RBуl1 = 12 Frl1.
Как видим, величина изгибающего момента не зависит от того, какими силами – левыми или правыми – пользуемся при его вычислении.
График (эпюра) изменения изгибающего момента M x по длине вала
показан на рисунке 16.2.
В горизонтальной плоскости (рис. 16.3) искривляется весь вал. Изгибающий момент M у считаем положительным, если он "создается" силой,
направленной вперед.
На участке АВ изгибающий момент изменяется от нуля (в сечении А) до наибольшего (положительного) Fмl2 , действующего в сечении B .
108
На участке DC воспользуемся правой силой RDX , направленной вперед: изгибающий момент в сечении D M у = 0, в сечении С Му = RDXl1 0. Соответствующая эпюра показана на рисунке 16.3.
16.4 Суммарный изгибающий момент
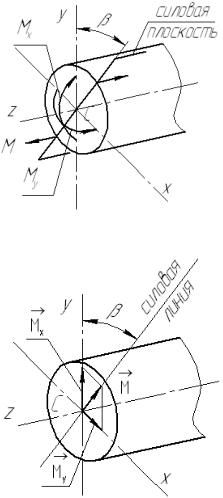
На рисунке 16.4 показаны изгибающие моменты (см. рис. 16.2 и 16.3), действующие во взаимно перпендикулярных плоскостях. Заметим, что их вовсе не обязательно изображать как пары сил, можно и так – дуговыми стрелками. Вообразим, что показанные на рисунке 16.4 стрелки изготовлены из гибкого материала, и прижмем их к плоскости поперечного сечения – получатся векторы
Мх и Му на рисунке 16.5. Их можно сложить по правилу параллелограмма,
заменив два изгибающих момента одним моментом М , равным их геометрической сумме. Оправдание этому сложению в приведении системы пар, то есть в замене нескольких пар одной парой.
Рисунок 16.4 – Изгибающие моменты в поперечном сечении вала
Рисунок 16.5 – Векторы изгибающих моментов складываются
геометрически
109
16.5 Нормальные напряжения в поперечном сечении вала
Нормальные напряжения в случае действия двух изгибающих моментов равны сумме нормальных напряжений (13.5) от каждого из моментов в отдельности:
σ = − |
М |
х |
у − |
М |
у |
х. |
(16.3) |
Ix |
Iу |
|
|||||
|
|
|
|
|
|
||
Изгибающие моменты в формуле (16.3) – см. рис. 16.6 и 16.5 – |
|
||||||
Мх = М cos β, |
Му = М sin β, |
(16.4) |
|||||
где β −угол наклона силовой линии (рис. 16.5), или силовой плоскости (рис.
16.4). Осевые моменты инерции круга |
|
Ix = Iу = Iu |
(16.5) |
(так как круг одинаково расположен относительно осей x и у). Формула (16.3) в
обозначениях (16.4) и (16.5): |
|
|
||
σ = − |
М cos β у − |
М sin β x = − M (xsin β + уcos β). |
(16.6) |
|
|
Iu |
Iu |
Iu |
|
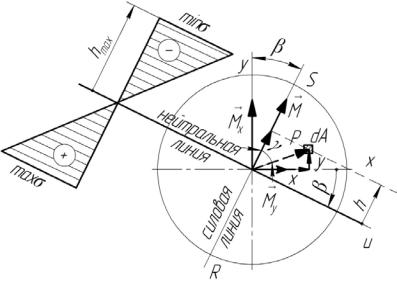
Выражение в скобках формулы (16.6) получается проектированием геометрической суммы х + у = ρ (рис. 16.6) на направление силовой линии:
хsin β + уcos β = ρcosγ = h,
и напряжения (16.6) |
|
σ = − M h. |
(16.7) |
Iu |
|
В точках прямой u , перпендикулярной к силовой линии, h = 0, напряжения (16.7) равны нулю – это нейтральная линия при изгибе. Наибольшие по модулю напряжения действуют в точках, наиболее удаленных от линии u , в точках S и R
(рис. 16.6):
σmax = |
M hmax = |
M |
, |
(16.8) |
|||
|
I |
u |
|
|
W |
|
|
|
|
Iu |
|
u |
|
|
|
Wu = |
|
|
|
(16.9) |
|||
hmax |
|
|
|||||
|
|
|
|
|
|
||
–момент сопротивления круглого сечения вала при изгибе.
16.6Осевой момент инерции и момент сопротивления круглого
сечения
Полярный момент инерции
I p = ∫ρ2dA, = ∫(х2 + у2 )dA= ∫x2dA+ ∫у2dA= Iу + Ix = 2Iu ,
A A A A
откуда осевой момент инерции площади круга (см. формулу (15.10))
110
Iu = 1 I p = πd 4 . 2 64
Момент сопротивления (16.9)
W |
= πd 4 / 64 |
= πd3 |
≈ 0,1d3. |
(16.10) |
|
u |
d / 2 |
32 |
|
|
|
|
|
|
|
||
Момент инерции и момент сопротивления сечения на участке со шпоночным пазом (рис. 16.1) находятся аналогично тому, как это сделано в п. 15.3, 15.4 (см.
формулы (15.11) и (15.15)):
Wu = |
πd3 |
− |
(вt1 )(d −t1 )2 |
(16.11) |
|
32 |
2d |
||||
|
|
|
Рисунок 16.6 – Нормальные напряжения и их эпюра при изгибе вала
16.7 Напряженное состояние в опасных точках поперечного сечения
вала
На рисунке 16.1 показан вал, работающий на изгиб с кручением. Наибольшие нормальные напряжения действуют (рис. 16.6) в точках R и S – точках пересечения окружности – границы сечения с силовой линией.
Наибольшие касательные напряжения действуют (рис. 15.4) в точках границы сечения, в точках R и S тоже. Наиболее опасные точки сечения – точки R и S . Напряжения в них (16.8) и (15.12)
σ |
max |
= |
M |
, |
||
|
|
|
W |
|
||
|
|
|
|
u |
(16.12) |
|
|
|
|
|
T |
||
τ |
max |
= |
, |
|||
Wp |
||||||
|
|
|
||||
где Т −крутящий момент.
111