kFL = 6 NF 0
NF
– коэффициент долговечности, определяемый отношением базового числа циклов NF 0 к расчетному числу циклов перемены напряжений NF , при постоянной
нагрузке NF = 60nT (T – срок службы передачи в часах, n – частота вращения слабого звена передачи). Если NF ≥ NF 0 , следует принять kFL =1.
14.5 Растяжение-сжатие бруса: скорость распространения продольной упругой волны
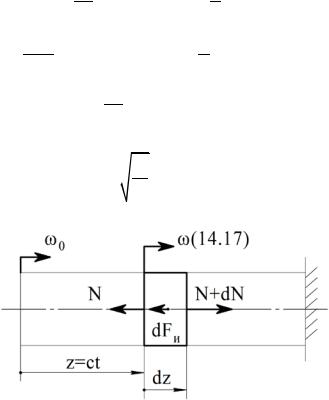
На рисунке 14.4 изображен защемленный брус, торцевое сечение которого колеблется по гармоническому закону
w0 =W0 sin Ωt .
Здесь Ω – круговая (циклическая) частота колебаний, W0 – их амплитуда.
Колебания поперечного сечения бруса, взятого на расстоянии z от торца, начнутся с опозданием (в момент z/c, где c – скорость распространения упругой волны):
|
z |
|
|
ω =W0 sin Ω t − |
|
. |
(14.17) |
|
|||
|
c |
|
|
Бесконечно близкие сечения, показанные на рисунке, колеблются, имея различные начальные фазы, следовательно, получают в один и тот же момент различные смещения ω и ω + dω. Удлинение выделенного на рисунке элемента равно в этот момент dw , относительное удлинение
ε = ddzω.
Нормальные напряжения в поперечном сечении бруса определяются законом Гука
σ = Eε = E ддωz ;
нормальная сила в сечении
N =σ A = EA ддωz .
Элемент бруса движется – нормальные силы на его торцах «уравновешиваются» силой инерции
dFи = ρAdz дд2tω2
( Adz – объем элемента, ρ – плотность материала бруса, ρAdz – масса элемента,
д2ω / дt2 – его ускорение):
dN = dFи ,
то есть
99
EA дд2zω2 dz = ρAdz дд2zω2 ,
E дд2zω2 = ρ дд2zω2 .
Используя здесь закон (14.17), получим
дд2zω2 = −c12 Ω2W0 sin Ω t − cz ,
дд2tω2 = −Ω2W0 sin Ω t − cz ,
E c12 = ρ ;
искомая скорость
c =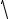 
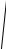Eρ .
Рисунок 14.4 – Колебания поперечных сечений
Лекция 15. Кручение круглого стержня
15.1 Угол сдвига
На рисунке 15.1 показан круглый стержень с продольными и поперечными линиями на поверхности. Рассмотрим деформацию стержня, при которой его продольная ось не удлиняется и не укорачивается, остается прямолинейной, а поперечные сечения стержня, оставаясь перпендикулярными к оси, поворачиваются вокруг оси как жесткие диски, не удаляясь друг от друга и не приближаясь друг к другу. На рисунке 15.1 показано, как деформируются первоначально прямоугольные элементы сетки линий. Эти элементы, становясь параллелограммами, получают сдвиг. Приращения (положительные и отрицательные) первоначально прямых углов называются углами сдвига.
100
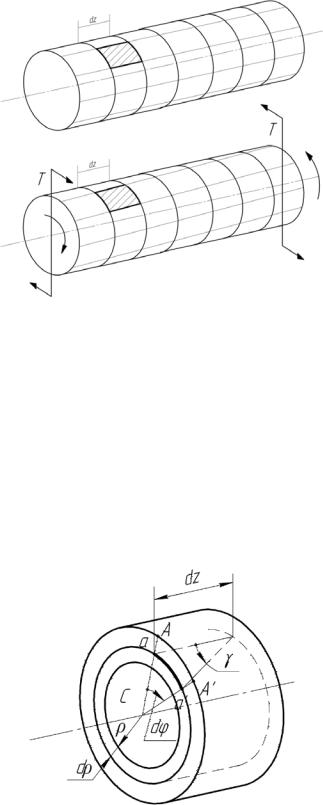
Рисунок 15.1 – Сдвиги прямоугольных элементов |
поверхности |
стержня в его кручении |
|
На рисунке 15.2 показан "вынутый" из стержня бесконечно короткий фрагмент стержня. Пусть переднее сечение (передний торец) фрагмента повернулось относительно заднего торца на угол закручивания dϕ. Любой из
радиусов CА переднего торца поворачивается на тот же угол. Мысленно
"вырежем" из фрагмента бесконечно тонкую трубку и найдем угол сдвига γ на ее поверхности:
γ = |
аа′ |
= Cadϕ |
= ρ dϕ . |
(15.1) |
|
dz |
dz |
dz |
|
Угол сдвига (15.1) пропорционален радиусу трубки.
Рисунок 15.2 – Угол сдвига на поверхности бесконечно тонкой трубки
15.2 Закон парности касательных напряжений
Рассмотрим теперь первоначально прямоугольный элемент трубки (рис. 15.3). Его сдвиг – результат действия касательных сил dT и dT′ на его гранях.
101
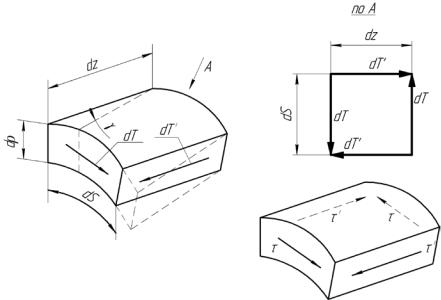
Касательные силы образуют две пары (см. вид по стрелке A), находящиеся в равновесии. Их моменты равны и противоположны по знаку:
dTdz − dT ds = 0. |
(15.2) |
′ |
|
Рисунок 15.3 – Сдвиг элемента трубки на рисунке 15.2, закон парности
касательных напряжений
Касательные силы в уравнении (15.2) равны произведениям касательных напряжений τ и τ′ на площади граней, где они действуют:
dT =τdsdρ, dT |
′ |
=τ dzdρ. |
(15.3) |
|
′ |
|
Вводя силы (15.3) в уравнение (15.2), найдем закон парности касательных
напряжений (рис. 15.3) |
(15.4) |
τ =τ . |
|
′ |
|
15.3 Распределение касательных напряжений при кручении
Закон Гука
τ =Gγ ,
где G −модуль сдвига материала стержня, дает (см. формулу (15.1)) линейное распределение касательных напряжений (рис. 15.4) вдоль любого из радиусов поперечного сечения стержня:
τ = K ρ, |
(15.5) |
где K – неизвестный пока коэффициент пропорциональности. |
Приведем |
касательные силы в поперечном сечении |
|
dT =τdA |
(15.6) |
к центру тяжести сечения C. Как видно на рисунке 15.4, любой из сил dT найдется "пара" – такая же сила, но направленная противоположно первой.
102
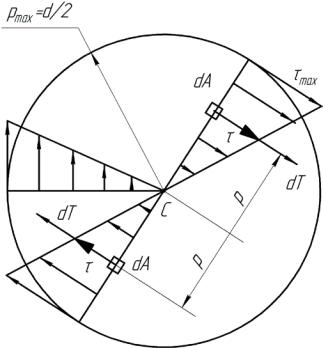
Рисунок 15.4 – Распределение касательных напряжений в сечении
закрученного стержня
Итак, система внутренних сил, действующих в поперечном сечении стержня, – система пар, приводящихся к одной паре. Ее момент (крутящий момент Т ) равен главному моменту сил (15.6)
T = ∫ρ(τdA).
A
Используя здесь напряжения (15.5), найдем: |
|
T = K ∫ρ2dA = KIР, |
(15.7) |
A |
|
где введена геометрическая характеристика круглого сечения |
|
IP = ∫ρ2dA, |
(15.8) |
A |
|
называемая полярным моментом инерции его площади.
К моменту (15.7) приводятся и внешние силы, действующие на часть стержня, расположенную перед "вынутым" фрагментом на рисунке 15.2. Внешние силы, действующие на торцы стержня, должны приводиться к парам, показанным на рисунке 15.1. Соответствующую деформацию называют кручением стержня.
Найдем, наконец, коэффициент K в формуле (15.5) и формулу для касательных напряжений при кручении: формулы (15.7) и (15.5) дают
K = |
T |
, |
τ = |
T |
ρ, |
(15.9) |
|
|
|||||
|
I p |
|
Iρ |
|
||
где полярный момент инерции круга (15.8, 11.13)
I p = |
πd 4 |
. |
(15.10) |
|
32 |
||||
|
|
|
||
|
|
103 |
|