
- •Лекция 1. Понятие о механизме
- •1.1 Классификация кинематических пар [2, с. 31]
- •1.2 Структурные формулы механизмов
- •1.3 Примеры плоских механизмов 3-го семейства
- •Лекция 2. Плоские механизмы с низшими парами V класса
- •2.1 Структурные группы Ассура
- •2.2 Структурные группы второго класса
- •2.3 Примеры групп других классов
- •2.4 Класс механизма
- •2.5 Класс рычажного 4-звенного механизма (рис. 1.10)
- •2.6 Пример
- •2.7 Плоские механизмы с высшими парами IV класса
- •Лекция 3. План скоростей плоского механизма
- •3.1 Условие существования кривошипа в четырехзвенных механизмах
- •3.2 План скоростей
- •3.3 Ошибки механизмов
- •Лекция 4. План ускорений плоского механизма
- •4.1 План ускорений кулисного механизма
- •4.2 План ускорений кривошипно-ползунного механизма
- •4.3 План ускорений кривошипно-коромыслового механизма
- •Лекция 5. Силовой анализ механизма
- •5.1 Силовой анализ группы Ассура
- •5.2 Силовой анализ ведущего звена
- •5.3 Ошибка положения из-за зазора в кинематической паре
- •Лекция 6. Электропривод
- •6.1 Передаточное отношение
- •6.2 Коэффициент полезного действия (КПД)
- •6.3 Выбор электродвигателя привода
- •6.4 Передаточные отношения передач привода
- •6.5 Мощности на валах привода; частоты вращения валов; моменты, вращающие валы
- •Лекция 7. Эвольвентное зацепление
- •7.1 Рабочие поверхности зубьев цилиндрических колес
- •7.2 Эвольвента круга и ее свойства
- •7.3 Эвольвентное зацепление
- •7.4 Передаточное отношение
- •7.5 Основные размеры эвольвентных колес
- •Лекция 8. Силы взаимодействия в эвольвентном зацеплении
- •8.1 Коэффициент торцевого перекрытия
- •8.2 Зацепление прямозубых колес
- •8.3 Зацепление косозубых колес
- •8.4 Силы в косозубом зацеплении
- •Лекция 9. Контактные напряжения в цилиндрических колесах
- •9.1 Удельная расчетная окружная сила
- •9.2 Контактные напряжения
- •9.3 Эквивалентное цилиндрическое прямозубое колесо
- •9.4 Условие прочности в контактном взаимодействии зубьев
- •9.5 Допускаемые контактные напряжения
- •Лекция 10. Передачи зацеплением с непараллельными валами
- •10.1 Конические передачи (с пересекающимися валами)
- •10.2 Эквивалентные цилиндрические колеса
- •10.3 Силы в зацеплении конических колес
- •10.4 Контактные напряжения, расчет на прочность
- •10.5 Червячная передача
- •10.6 Силы в червячной передаче
- •Лекция 11. Геометрические характеристики плоских фигур
- •11.1 Статические моменты площади
- •11.2 Моменты инерции
- •11.3 Геометрические характеристики простейших фигур
- •11.4 Брус (стержень)
- •Лекция 12. Внутренние силовые факторы в поперечном сечении бруса
- •12.1 Внутренние силовые факторы
- •12.2 Внутренние силовые факторы в поперечном сечении вала редуктора
- •12.3 Напряженное состояние в точке бруса (рис. 12.1)
- •12.4 Выражение внутренних силовых факторов через напряжения в поперечном сечении бруса
- •Лекция 13. Нормальные напряжения в поперечном сечении
- •13.1 Гипотеза плоских сечений
- •13.2 Гипотеза о ненадавливании продольных волокон
- •13.3 Закон Гука
- •13.5 Принцип независимости действия сил
- •13.6 Простые и сложные деформации бруса
- •13.7 Условие прочности при растяжении (сжатии)
- •13.8 Нормальные напряжения при прямом изгибе
- •Лекция 14. Нормальные напряжения в статических и динамических задачах
- •14.1 Нормальные напряжения смятия в шпоночных соединениях
- •14.2 Нормальные напряжения при изгибе прямых зубьев зубчатых передач
- •14.3 Нормальные напряжения при изгибе косых зубьев
- •14.4 Открытая зубчатая передача: проектный расчет
- •14.5 Растяжение-сжатие бруса: скорость распространения продольной упругой волны
- •Лекция 15. Кручение круглого стержня
- •15.1 Угол сдвига
- •15.2 Закон парности касательных напряжений
- •15.3 Распределение касательных напряжений при кручении
- •15.4 Моменты сопротивления при кручении
- •15.5 Расчет на прочность
- •Лекция 16. Напряженное состояние вала
- •16.1 Расчетная схема
- •16.2 Опорные реакции
- •16.3 Изгибающие моменты
- •16.4 Суммарный изгибающий момент
- •16.5 Нормальные напряжения в поперечном сечении вала
- •Лекция 17. Упрощенное плоское напряженное состояние (УПНС)
- •17.1 Напряженное состояние в точке
- •17.2 Чистый сдвиг
- •17.3 Нормальные и касательные напряжения в УПНС
- •17.6 Критерий прочности Треска, Сен-Венана
- •17.7 Коэффициент безопасности в УПНС
- •Лекция 18. Циклически изменяющиеся нормальные и касательные напряжения в поперечном сечении вала
- •18.1 Предел выносливости при симметричном цикле
- •18.2 Произвольный цикл напряжений
- •18.3 Диаграмма предельных амплитуд
- •18.4 Запас выносливости
- •18.5 Запасы выносливости вала
- •18.6 Запасы в опасных сечениях вала
- •Лекция 19. Подшипники качения
- •19.1 Основные типы подшипников качения
- •19.2 Серии диаметров и ширин [4, с. 330–331]
- •19.3 Точность подшипников качения [4, c. 331]
- •19.4 Цифровые обозначения подшипников
- •19.5 Выбор типа подшипника
- •19.6 Проверка подшипника на статическую грузоподъемность
- •19.7 Проверка подшипников на долговечность
- •19.8 Схемы установки подшипников
- •19.9 Смазка подшипников закрытых передач
- •Лекция 20. Ременные передачи
- •20.1 Кинематика ременной передачи
- •20.2 Геометрия ременной передачи
- •20.3 Силы в передаче
- •20.4 Формула Эйлера
- •20.5 Фактор трения
- •Лекция 21. Напряжения в ремне
- •21.1 Напряжения от центробежных сил
- •21.2 Напряжения при изгибе ремня
- •21.3 Напряжения в ремне
- •21.4 Расчет клиноременной передачи
- •21.5 Допускаемое полезное напряжение
- •21.6 Силы, действующие на валы ременной передачи
- •Лекция 22. Цепная передача
- •22.1 Конструкция втулочно-роликовой цепи и звездочек
- •22.2 Передаточное число
- •22.3 Удары в передаче
- •22.4 Износ цепи
- •22.5 Оптимальное число зубьев
- •22.6 Давление в шарнирах цепи
- •22.7 Допускаемое давление в шарнирах цепи
- •22.8 Практический расчет цепной передачи
- •Лекция 23. Резьбовые соединения
- •23.1 Крепёжные и ходовые резьбы
- •23.2 Основные виды резьбовых соединений
- •23.3 Амонтоново трение
- •23.4 Трение в резьбе
- •23.5 Резьба метрическая
- •23.6 Расчёт затянутого болта на прочность
- •Лекция 24. Расчетные схемы механической части электропривода
- •24.1 Приведение масс
- •24.2 Приведение сил
- •24.3 Приведение жесткостей механических связей
- •24.4 Двухмассовая упругая система
- •24.5 Пуск двигателя
- •Литература
|
|
|
|
|
|
|
|
|
(Ka′)3/2 |
2 |
|
|
|
|
|||
a |
= |
z |
2 |
+1 |
|
|
|
|
T K |
|
, |
(10.11) |
|||||
|
|
|
3 |
|
|
|
|
|
|
|
|||||||
q |
|
z2 |
|
|
|
||||||||||||
W |
|
|
|
|
|
[σH ] |
|
2 |
H |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
q |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
коэффициент
(Ka′)3/2 =5400
(при Т2 в Н∙м, [σH ] в МПа, а в мм, стальном червяке, бронзовом (чугунном) венце
колеса). Требуемое условием контактной выносливости расстояние (10.11) позволяет вписать передачу в стандартное межосевое расстояние.
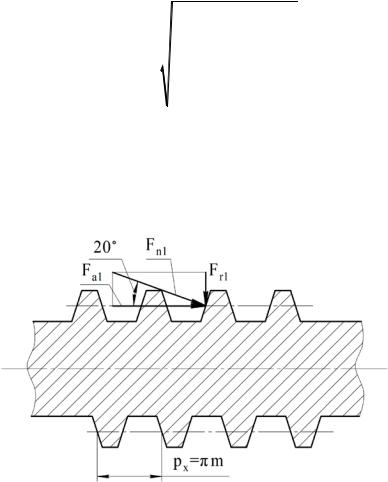
Рисунок 10.7 – Осевой шаг нарезки архимедова червяка;
силы, действующие на червяк
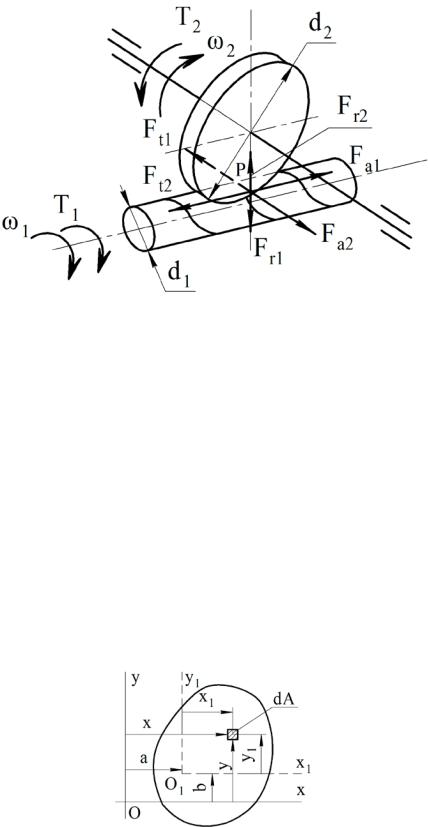
10.6 Силы в червячной передаче
На рисунке 10.8 показана окружная сила
Ft1 = |
2T1 |
(10.12) |
|
d1 |
|
на червяке (с правой нарезкой) (создающая момент, уравновешивающий вращающий момент Т1) и окружная сила на колесе
Ft 2 |
= |
2T2 |
(10.13) |
|
|
d2 |
|
(создающая момент, движущий колесо). Сила (10.12) имеет пару во взаимодействии червяка с колесом – осевую силу на колесе:
Fa2 = Ft1 ;
сила (10.13) – осевую силу на червяке:
Fa1 = Ft 2 .
71
Радиальные силы раздвигают червяк и колесо. Радиальная сила на червяк (рис.
10.7)
Fr1 = Fa1 tg20° = Ft 2tg20°.
Такая же радиальная сила действует на колесо.
Рисунок 10.8 – Сила в червячном зацеплении
Лекция 11. Геометрические характеристики плоских фигур
11.1 Статические моменты площади
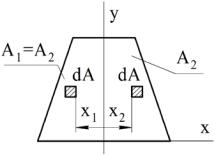
Рассмотрим (рис.11.1) произвольную плоскую фигуру, отнесенную к осям x, y. Статические моменты площади фигуры
Sx = ∫ydA, |
Sy = ∫xdA , |
(11.1) |
A |
A |
|
где интегрирование распространяется на всю площадь фигуры А. Поскольку ординаты y и абсциссы x элементов площади dA могут быть как положительными, так и отрицательными, статические моменты (11.1)
Sx >< 0, Sy >< 0.
Если статический момент, например, Sx равен нулю, ось x – центральная (содержащая центр тяжести фигуры).
Рисунок 11.1 – К написанию формул (11.2)
72
Перейдем к новым |
осям x1 , |
y1 , параллельным прежним осям x, y. |
|
Преобразование координат производится по формулам (рис. 11.1) |
|||
|
x1 |
= x − a, |
(11.2) |
|
y1 = y −b . |
||
|
|
||
Используем формулы (11.2) в определениях (11.1): |
|||
Sx1 = ∫y1dA = ∫(y −b)dA = ∫ydA −b∫dA = Sx −bA, |
|||
A |
A |
A |
A |
Sy1 = Sy − aA .
Пусть оси x1 , y1 центральные, О1 – центр тяжести фигуры. Координаты центра тяжести в осях x, y
xc = a = |
Sy |
, |
yc =b = |
S |
x |
. |
(11.3) |
A |
|
|
|||||
|
|
|
A |
|
|||
Если центр тяжести фигуры известен, статические моменты фигуры относительно произвольных осей х, у
Sx = Ayc , |
Sy = Axc . |
(11.4) |
Формулы (11.3), (11.4) можно использовать в определении координат центра тяжести составных фигур:
|
|
|
|
|
n |
|
|
|
|
n |
|
y |
= |
S |
|
= |
∑Ak yck |
, x |
= |
Sy |
= |
∑Ak xck |
, |
x |
k=1 |
k=1 |
|||||||||
|
c |
A |
|
n |
c |
|
A |
|
n |
|
|
|
|
|
∑Ak |
|
|
|
∑Ak |
|
|||
|
|
|
|
|
k=1 |
|
|
|
|
k=1 |
|
где Ak , yck , xck – площадь и координаты центра тяжести k-ой части фигуры, n –
число частей.
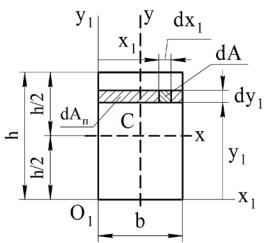
Если фигура симметрична (рис. 11.2), ее статический момент относительно оси симметрии равен нулю, ось симметрии – центральная ось. Действительно,
Sy = ∫xdA = ∫x1dA + ∫x2dA = ∫(−x2 )dA + ∫x2dA = 0.
A |
A1 |
A2 |
A2 |
A2 |
Рисунок 11.2 – Симметричная фигура
11.2 Моменты инерции
Геометрические характеристики второго порядка – моменты инерции:
осевые
73

Ix = ∫y2dA > 0 , |
Iy = ∫x2dA > 0 |
(11.5) |
A |
A |
|
и центробежный |
|
|
Ixy = ∫xydA<>0. |
(11.6) |
|
A |
|
|
перейдем в интегралах (11.5, 11.6) от координат х, у к координатам (11.2) при учете определений (11.1):
Ix1 = ∫y12dA = ∫(y −b)2 dA = ∫y2dA − 2b∫ydA +b2 ∫dA = Ix − 2bSx +b2 A,
A |
A |
A |
A |
A |
|
|
Ix1y1 = ∫x1 y1dA = ∫(x − a)(y −b)dA = ∫xydA − a∫ydA −b∫xdA + ab∫dA = |
(11.7) |
|||||
A |
A |
A |
A |
A |
A |
|
= Ixy − aSx −bSy + abA.
Если оси x , y центральные, статические моменты Sx ,Sy равны нулю: моменты инерции (11.7)
Ix = Ix +b2 A , |
Iy = Iy + a2 A, |
Ix y = Ixy + abA. |
(11.8) |
|
1 |
1 |
1 |
1 |
|
При переходе от центральных осей к нецентральным осевые моменты инерции (11.8) возрастают, центральный момент инерции (11.8) может возрасти, но может и уменьшиться (в зависимости от знаков координат a,b нового начала О1, в
прежних осях x , y).
Центробежный момент инерции относительно осей, одна из которых ось симметрии, равен нулю. В общем случае всегда найдется пара взаимно перпендикулярных осей u, v, относительно которых Iuv = 0 . Такие оси называются
главными. Главные оси найдутся и среди центральных, они называются главными центральными (естественными) и играют в прикладной механике важную роль.
11.3 Геометрические характеристики простейших фигур
К простейшим относим прямоугольник и круг. Рассмотрим (рис. 11.3) прямоугольник и найдем координаты его центра тяжести. Статические моменты бесконечно узкой полоски, показанной на рисунке,
dSx1 = ∫ y1 (dy1dx1 )= y1dy1 ∫b dx1 =by1dy1 ,
dAП |
0 |
(размер полоски dy1 и ординату y1 |
выносим за знак интеграла, поскольку у всех |
элементов полоски эти величины одинаковы). Статический момент прямоугольника
Sx1 = ∫dSx1 =∫h by1dy1 |
= bh2 |
, |
|
A |
0 |
2 |
|
ордината центра тяжести
y1c = Sx1 = bh2 = h ,
A 2bh 2
74
абсцисса центра тяжести, очевидно,
x1c = b2 .
Центр тяжести прямоугольника находится на пересечении его диагоналей.
Рисунок 11.3 – Прямоугольное сечение
Центробежный момент инерции полоски |
|
||||
dIx1y1 = ∫ x1 y1dx1dy1 = y1dy1 ∫b x1dx1 |
= y1 b2 |
dy1 , |
|||
dAП |
|
|
0 |
2 |
|
|
|
|
|
||
Ix1y1 = ∫dIx1y1 = ∫h y1 b2 |
dy1 = b2h2 . |
|
|||
A |
0 |
2 |
|
4 |
|
Найдем центробежный момент инерции относительно осей x1 , y. Оси x1 , y1 не центральные, воспользуемся формулой (11.7):
Ix y = Ix y − |
b |
Sx |
−0 Sy + |
b |
0 A = |
b2h2 |
− |
b |
|
bh2 |
= 0. |
|||
2 |
2 |
4 |
2 |
2 |
||||||||||
1 |
1 |
1 |
1 |
1 |
|
|
|
|
||||||
Результат очевидный, ибо ось y – ось симметрии прямоугольника. Таким же будет центробежный момент инерции относительно центральных осей x и y – это главные центральные оси.
Найдем главные оси в точке О1. На рисунке 11.4 показаны произвольные оси u и v. Новые координаты элемента площади dA находятся из рассмотрения заштрихованных треугольников:
u= x1 cosα + y1 sinα , v = −x1 sinα + y1 cosα .
Моменты инерции относительно новых осей u и v
Iu = ∫v2dA = ∫(−x1 sinα + y1 cosα)2 dA =(sinα)2 ∫x12dA −(2sinα cosα)
A |
A |
|
A |
(11.9) |
|
∫x1 y1dA +(cosα)2 |
∫y12dA = Iy1 sin2 |
α − Ix1y1 sin 2α + Ix1 cos2 |
|||
α, |
|||||
A |
|
A |
|
|
|
75
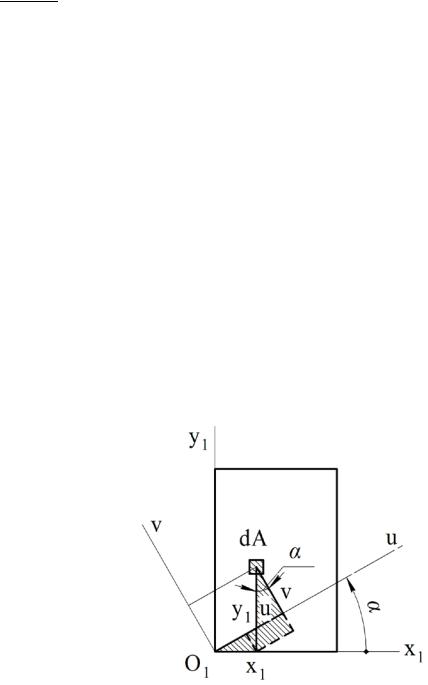
Iuv = ∫uvdA = ∫(x1 cosα + y1 sinα)(−x1 sinα + y1 cosα)dA =
AA
=−(cosαsinα)∫x12dA −(sin2 α)∫x1 y1dA + cos2 α∫x1 y1dA +(cosαsinα)∫y12dA =
A A A A
= Ix1 −2 Iy1 sin 2α + Ix1y1 cos2α.
Если оси u и v – главные, центробежный момент инерции
Iuv = 0 ;
угол, определяющий направление главных осей, находится из уравнения
|
2Ix y |
||
tg2α = − |
|
1 1 |
. |
Ix |
|
||
|
− Iy |
||
|
1 |
1 |
|
Покажем, что осевой момент инерции (11.9) относительно главной оси экстремален: производная, отвечающая экстремуму функции Iu (α),
dIu =(2sinα cosα)Iy1 − 2Ix y |
cos2α −(2cosαsinα)Ix = 0 , |
|
||||||
dα |
1 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
откуда |
|
|
|
2Ix y |
|
|
||
|
|
|
|
|
|
|||
|
tg2α = − |
|
1 |
1 |
. |
|
(11.10) |
|
|
|
|
|
|
||||
|
|
|
|
Ix − Iy |
|
|
||
|
|
|
1 |
1 |
|
|
|
|
Уравнению (11.10) удовлетворяют |
|
два |
значения угла α : α1 |
и α2 =α1 +90°. |
||||
Действительно, |
|
|
|
|
|
|
|
|
tg2α2 = tg2(α1 +90°)= tg(2α1 +180°)= tg2α1 .
Рисунок 11.4 – Преобразование координат при повороте осей
Уравнению (11.10) удовлетворяют два значения угла α : α1 и α2 =α1 +90°. Действительно,
tg2α2 = tg2(α1 +90°)= tg(2α1 +180°)= tg2α1 .
76
Угол α1 , определяющий взаимно перпендикулярные оси экстремальных моментов инерции Imax , Imin , совпадают с углом, определяющим пару главных осей. Оси x, y на рисунке 11.3 – главные оси. Относительно одной из них момент инерции (Ix )
максимален. Относительно другой (Iy ) минимален. Найдем их (рассматривая рисунок 11.3):
h/2 |
2 |
= |
by3 |
|
h/2 |
|
|
||||||
Imax = Ix = ∫ |
(bdy1 )y1 |
|
1 |
|
|
|
−h/2 |
|
|
|
3 |
|
−h/2 |
|
hb3 |
|
||||
Imin = Iy = |
|
|
||||
12 |
. |
|
|
|||
|
|
|
|
|
||
= |
bh3 |
, |
|
12 |
|||
|
(11.11) |
||
|
|
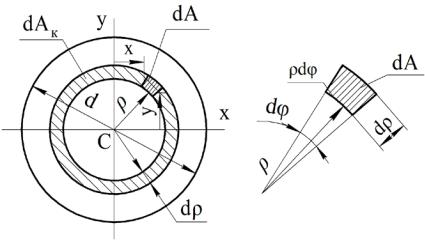
Займемся кругом (рис. 11.5). Все центральные оси его главные. Главные центральные моменты инерции круга
Ix = ∫y2dA, |
Iy = ∫x2dA |
|
|
равны. Сложим их: |
A |
A |
|
(y2 + x2 )dA = ∫ρ2dA = I p , |
|
||
Ix + Iy = ∫ |
(11.12) |
||
A |
|
A |
|
где последний интеграл называется полярным моментом инерции круга.
Рисунок 11.5 – К вычислению полярного момента инерции (11.13)
Выделим в круге бесконечно узкое кольцо. Его полярный момент инерции dIρ = ∫ ρ2 (dρρdϕ)= ρ3dρ2∫π dϕ = 2πρ3dρ,
dAk |
0 |
полярный момент инерции круга в целом
Iρ = ∫dIρ = d∫/2 |
2πρ3dρ = |
πρ4 |
|
d /2 |
= |
πd 4 . |
(11.13) |
|
|
||||||||
A |
0 |
|
2 |
|
0 |
|
32 |
|
|
|
|
|
|
|
|||
Деля момент инерции (11.13) на 2 – см. сумму (11.12), – получим формулу для главного центрального момента инерции круга:
77
