[σсм] – допускаемое напряжение на смятие того из материалов деталей или болта, который слабее. Условие равнопрочности всех частей соединения на рисунке
23.16
h2 = 2h1.
Требуемый диаметр болта находится из обоих условий, принимается больший из них.
Рисунок 23.16 – Болт, вставленный в отверстия деталей без зазора, работает
на срез и смятие
Лекция 24. Расчетные схемы механической части электропривода
Кинематические схемы приводов (вроде тех, что изображены на рисунках 24.2, 24.4) не отражают податливости всех элементов кинематических цепей (под нагрузкой все они деформируются в той или иной степени). Вместе с этим невозможно сравнивать массы элементов привода, движущиеся с различными скоростями. То же относится и к силам, действующим на них.
Именно, поэтому необходимы расчетные механические схемы приводов, в которых массы (и моменты инерции), силы (и моменты) и жесткости механических связей заменены эквивалентными величинами, приведенными к одной и той же расчетной скорости (обычно к угловой скорости ротора двигателя).
Основные требования [5, с. 20] при этом: сохранение запаса потенциальной энергии деформаций механических связей и кинетической энергии системы, а также мощностей (работ в единицу времени), действующих в системе сил и моментов.
24.1 Приведение масс
Из равенства кинетических энергий
Iкпр2ω12 = Iк2ωк2
161
находим приведенный момент инерции к-ой массы, вращающейся с угловой скоростью ωк :
I |
|
= |
I |
ω |
2 |
= |
|
I |
к |
= |
I |
к |
, |
|
|||
кпр |
|
к |
|
к |
|
|
|
|
|||||||||
|
ω12 |
|
|
ω |
|
|
|
(24.1) |
|||||||||
|
|
|
|
|
|
2 |
|
i12 |
к |
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωк |
|
|
|
|
|
|
|
|
где ω1 – угловая скорость |
|
ротора |
|
двигателя, i1 к =ω1 / ωк |
– передаточное |
||||||||||||
отношение от вала двигателя (вала приведения) к к-му валу вращающейся массы. В случае j-ой массы, движущейся поступательно (со скоростью Vj ),
|
|
|
|
I |
|
|
ω2 |
|
|
m V 2 |
|
|
|
|
||
|
|
|
|
|
j пр 1 |
= |
|
|
j |
j |
|
, |
|
|
||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
2 |
|
|
||
|
|
|
|
|
2 |
|
|
|
Vj |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
I |
jпр |
= |
mjVj |
|
= m |
|
|
|
= m ρ2 |
, |
||||||
ω2 |
|
ω |
|
|||||||||||||
|
|
|
|
j |
|
|
|
j |
1 j |
|
||||||
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|||
где ρ1 j =Vj / ω1 – радиус приведения массы mj .
24.2 Приведение сил
Из равенства мощностей
Mпркω1 = Mкωк
находим приведенный вращающий момент:
Mпрк = |
Mкωк |
= |
|
Mк |
|
= |
Mк |
. |
|
|
|
|
|
||||||
|
|
ω1 |
|
|
(24.2) |
||||
|
ω1 |
|
i1к |
||||||
|
|
|
|
ωк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приведенная сила в поступательном движении j-го звена
|
F V |
j |
V |
j |
|
|
|
Fпр j = |
j |
= Fj |
|
|
= Fjρ`1 j . |
||
ω1 |
|
ω1 |
|||||
|
|
|
|
|
|||
24.3 Приведение жесткостей механических связей
Полагая связь упругой (подчиняющейся (рис. 24.1) закону Гука), найдем потенциальную энергию деформаций связи – она равна работе «момента» Т на угловом перемещении – угле «закручивания» φ (площади графика на рисунке
24.1):
U = 12 (C∆ϕ)∆ϕ = 12 C (∆ϕ)2 ,
где С – жесткость связи (коэффициент пропорциональности в законе Гука), φ – «угол закручивания» связи. Из равенства потенциальных энергий
12 Cкпр (∆ϕ1 )2 = 12 Cк (∆ϕк )2 ,
162
Рисунок 24.1 – К вычислению потенциальной энергии деформаций
упругой связи
находим приведенную жесткость к-ой связи, работающей на кручение:
C |
|
= |
C |
к |
(∆ϕ |
к |
)2 |
= |
|
C |
к |
|
= |
C |
к |
, |
|
кпр |
(∆ϕ1 )2 |
|
|
|
2 |
|
|
(24.3) |
|||||||||
|
|
|
|
∆ϕ |
|
i12к |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ϕк |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где отношение угловых перемещений равно передаточному отношению i1к . В случае связи, работающей на растяжение–сжатие:
|
|
1 C |
(∆ϕ )2 = |
1 C |
|
( |
∆l |
)2 , |
|
|
|
||||||
|
|
2 1 |
|
1 |
|
|
2 |
|
к |
|
|
к |
|
|
|
(24.4) |
|
C |
|
Cк (∆lк )2 |
=C |
|
|
∆l |
к |
|
2 |
=C |
|
2 |
|||||
= |
|
|
|
|
к |
|
|
|
|
ρ |
|
. |
|||||
(∆ϕ1 ) |
2 |
|
|
|
|
|
|
||||||||||
1 |
|
|
|
∆ϕ1 |
|
к |
1к |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
24.4 Двухмассовая упругая система
Обратимся к кинематической схеме привода вентилятора (рис. 24.2).
Рисунок 24.2 – Кинематическая схема электропривода вентилятора: Д – ротор двигателя, СМ – упругая соединительная муфта, В – рабочее колесо вентилятора
Расчетные механические схемы представлены на рисунке 24.3. На нем (схема а) показаны относительно большие массы ротора двигателя и рабочего
колеса вентилятора (с моментами инерции I1 , I4 ), сравнительно небольшие массы полумуфт I2 , I3 , относительно высокие жесткости валов двигателя и
рабочего колеса C1 , C3 и жесткость наиболее податливой связи полумуфт C2 . Представление о моментах инерции дают размеры соответствующих элементов
163
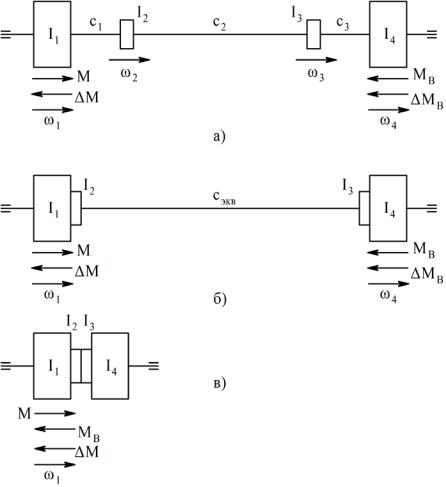
схемы, о податливостях безмассовых механических связей – длины соответствующих отрезков вала.
Имея в виду, что движение многомассовых упругих систем, в основном, определяется наибольшими массами и наименьшими жесткостями, перейдем к рассмотрению двухмассовой упругой системы (схема б). В ней наибольшие массы
I1 и I4 объединены с массами полумуфт I2 и I3 (сравнительно небольшими
отличиями скоростей ω2 и ω3 от скоростей ω1 и ω4 пренебрегаем), податливости валов суммируются:
1 |
= |
1 |
+ |
1 |
+ |
1 |
. |
|
|
||||
|
C |
|
C |
C |
|
|
|
|
|||||
|
экв |
|
|
2 |
|
C |
|
|
|||||
|
|
|
1 |
|
|
|
3 |
|
1 |
|
|||
В некоторых задачах возможно пренебречь податливостью |
(полагая |
||||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Cэкв |
||
эквивалентную жесткость Cэкв бесконечно большой) и рассматривать (схема в)
жесткое приведенное механическое звено.
Заметим [5, с. 25]: двухмассовая схема (б) достаточно хорошо заменяет реальную систему (рис. 24.2), чего нельзя сказать о схеме в.
Рисунок 24.3 – Расчетные механические схемы электропривода
вентилятора: М – момент, развиваемый двигателем, МВ – момент полезного сопротивления на рабочем колесе, М и МВ – моменты потерь на трение в подшипниках
164