S2 = Ft |
|
1 |
|
, |
|
|||||||
e f α −1 |
|
|||||||||||
S |
|
= F |
|
|
|
e f α |
, |
|
(20.12) |
|||
|
|
|
|
|
|
|
|
|||||
1 |
|
t e f α −1 |
|
|
|
|||||||
S |
|
= |
1 |
F |
|
e f α +1 |
. |
|||||
|
2 |
|
|
|
|
1 |
||||||
|
0 |
|
|
|
t e f α − |
|
||||||
20.5 Фактор трения
Назовем произведение fα фактором трения и найдем, что при fα→0 все силы (20.12) становятся бесконечно большими; передача полезной нагрузки становится невозможной. Передача работает тем лучше, чем больше фактор трения fα. Увеличить его можно, используя натяжной ролик (рис. 20.7) или повышая трение в передаче.
На рисунке 20.8 показан фрагмент клинового ремня в канавке (ручье) шкива. Силы трения действуют на конических поверхностях ручья. Нормальные реакции этих поверхностей, возникающие под давлением на фрагмент (см. силу dP), находятся из уравнения равновесия фрагмента
2dN sin ϕ2 = dP :
dN = dPϕ . 2sin 2
Рисунок 20.7 – Передача с натяжным роликом
Рисунок 20.8 – Силы трения в клиноременной передаче
138
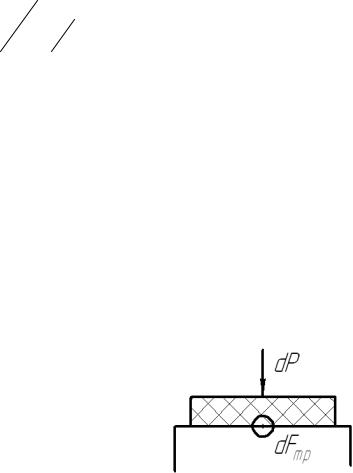
Суммарная сила трения |
|
|
|
|
|
|
|
|
|
|
f |
|
|
′ |
dFтр = 2 fdN = |
|
ϕ |
|
|
|
dP = f dP, |
|||
|
|
2 |
|
|
sin |
|
|
||
где f ′ = |
f |
ϕ |
– приведенный коэффициент трения. |
|
sin |
|
2 |
В плоскоременной передаче (рис. 20.9) dFтр = fdP.
Для стандартных клиновых ремней φ = 40°, f´ / f ≈ 3. Трение в клиноременной передаче примерно в 3 раза больше трения в плоскоременной передаче.
Соответственно, угол обхвата (20.4) в клиноременной передаче может быть снижен до 120° (и даже до 90°) против α ≥ 150° в плоскоременной передаче; межосевое расстояние может быть снижено:
0,55(D1 + D2 ) + h ≤ a ≤ 2(D1 + D2 ), |
(20.13) |
где h – толщина ремня (рис. 20.2), против
a ≥ 2(D1 + D2 );
передаточное число (отношение), наоборот, может быть увеличено до 7 (даже до 10) – против u ≤ 5 плоскоременной передачи.
Рисунок 20.9 – Сила трения в плоскоременной передаче
Лекция 21. Напряжения в ремне
21.1 Напряжения от центробежных сил
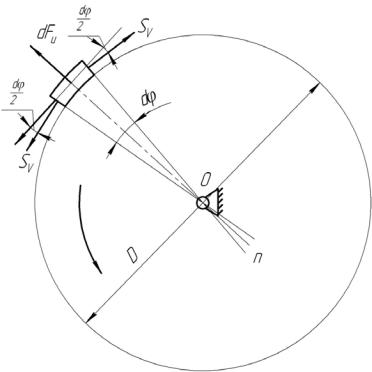
Всякий бесконечно короткий фрагмент (элемент) ремня, огибая любой из шкивов, движется по окружности – испытывая воздействие центробежных сил инерции dFи (рис. 21.1). Дополнительное натяжение ремня находится из уравнения проекций на нормаль к поверхности шкива:
−dF |
+ |
2S |
v |
sin |
dϕ |
|
= |
0, |
(21.1) |
|||
|
|
|
||||||||||
и |
|
|
|
|
2 |
|
|
|
|
|
||
где сила инерции |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
2 |
|
|
dFи = |
γ |
|
A D dϕ |
|
|
|
, |
|||||
|
|
D |
/ 2 |
|||||||||
|
g |
|
|
2 |
|
|
|
|||||
|
|
|
|
|
|
139 |
|
|
|
|
|
|
γ / g – плотность материала (γ – удельный вес, g – ускорение свободного падения), А – площадь поперечного сечения, 0,5Ddφ – длина элемента ремня, в
скобках масса элемента, V 2 / (D / 2) |
|
– центростремительное ускорение; синус |
||||||
бесконечно малого угла dϕ / 2 может быть заменен углом dϕ / 2 (см. п. 20.4). |
||||||||
Уравнение (21.1) переписывается: |
|
|||||||
|
γ |
Adϕ |
|
2 |
= Svdϕ; |
|
||
|
|
V |
|
|||||
g |
|
|
|
|
|
|
||
дополнительное натяжение ремня |
γ AV 2 , |
|
||||||
|
|
Sv = |
(21.2) |
|||||
напряжения в ремне |
|
|
|
g |
|
|
|
|
|
|
|
Sv |
|
|
γ V 2. |
|
|
|
|
σv = |
|
|
= |
(21.3) |
||
|
|
|
A |
|||||
|
|
|
|
|
g |
|
||
Дополнительное натяжение (21.2) ослабляет контакт ремня со шкивами, уменьшая силы трения и снижая нагрузочную способность передачи. Однако, снижение это заметно только при высоких скоростях ремня (V > 25м/с).
Рисунок 21.1 – Центробежная сила и дополнительное натяжение
21.2 Напряжения при изгибе ремня
Ремень, огибая любой из шкивов, искривляется – изгибается. На рисунке 21.2 показан бесконечно короткий фрагмент (элемент) ремня. Наибольшее удлинение получает наружный слой ремня:
140
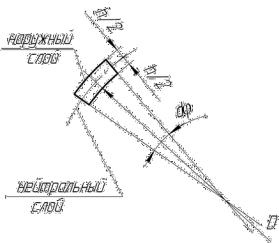
ε |
|
= (D / 2 + h)dϕ −(D / 2 + h / 2)dϕ |
= |
h / 2 |
≈ |
h |
max |
|
|
||||
|
(D / 2 + h / 2)dϕ |
|
(D / 2 + h / 2) |
|
D |
|
|
|
|
|
(так как толщина ремня h много меньше диаметра шкива). Наибольшие напряжения при изгибе ремня (по закону Гука)
σи = Eεmax = E |
h |
. |
(21.4) |
|
|||
|
D |
|
|
Напряжения (21.4) не играют никакой полезной роли, более того они, как увидим далее, – главная причина разрушения ремня от усталости.
Напряжения (21.4) можно снизить, если увеличить отношение D
h . Его рекомендуемые значения для плоских ремней
40 ≥ Dh1 ≥30,
для клиновых ремней
20 ≥ Dh1 ≥15.
Рисунок 21.2 – Элемент ремня при его изгибе на шкиве
21.3 Напряжения в ремне
Разность натяжений ветвей ремня (20.6, 20.7) равна с друг ой стороны полезной нагрузке (20.9): дополнительное усилие к предварительному натяжению ремня
∆S = Ft / 2,
то есть натяжения (20.6, 20.7) ветвей ремня
|
|
|
S = S |
0 |
+ |
1 F , |
|
|
|
|
|
||||||||
|
|
|
|
1 |
|
|
|
|
2 |
t |
|
|
|
|
|
(21.5) |
|||
|
|
|
S |
|
= S |
|
|
|
1 F |
|
|
|
|
|
|||||
|
|
|
|
|
|
− |
; |
|
|
|
|
|
|||||||
соответствующие напряжения |
|
2 |
|
|
|
0 |
|
|
2 |
t |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
σ |
1 |
= |
S0 |
|
+ |
1 |
Ft |
|
=σ |
0 |
+ |
1 |
σ |
F |
, |
(21.6) |
|||
|
|
A |
|
|
2 A |
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
141 |
|
|
|
|
|
|
|
σ |
2 |
=σ |
0 |
− |
1 |
σ |
F |
, |
(21.7) |
где |
|
|
2 |
|
|
|
|||
σ0 = S0 / |
А |
|
|
(21.8) |
|||||
|
|
|
|||||||
– напряжение предварительного натяжения, σF = Ft / А– полезное напряжение.
Наибольшие напряжения получим, если к напряжениям (21.6) добавим напряжения (21.4) (напряжения (21.3) считаем пренебрежимо малыми):
σmax =σ0 + |
σF |
+σи; |
(21.9) |
|
|
||||
наименьшие напряжения |
2 |
|
|
|
|
σF |
|
||
σmin =σ0 |
− |
(21.10) |
||
|
|
2 |
|
|
равны напряжениям (21.7).
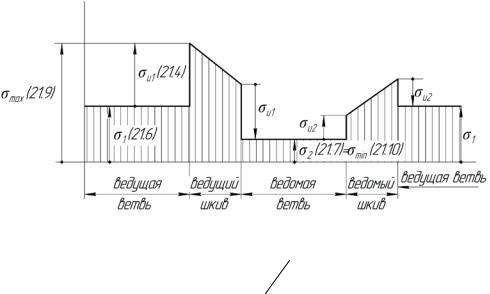
На рисунке 21.3 показан цикл напряжений в поперечном сечении ремня. Напряжения σи, возникая в момент набегания ремня на шкив и исчезая в момент сбегания ремня со шкива, делают напряжения в ремне изменяющимися циклически. Вместе с этим возникает проблема долговечности ремня. Выдерживая до усталостного разрушения определенное число циклов – пробегов, ремень тем долговечнее, чем меньше число его пробегов в единицу времени
ν = V , |
(21.11) |
L
где L – длина ремня (20.5). Плоские ремни допускают [ν] = 5 с-1, клиновые [ν] = = 20 с-1.
Рисунок 21.3 – Циклически изменяющиеся напряжения в ремне: напряжения при изгибе на ведущем шкиве (21.4), напряжения при изгибе
на ведомом шкивеσи2 = Eh D2 <σи1
Уравнение кривой выносливости ремня (ремней)
σmaxm N = const,
где σmax – наибольшее напряжение в ремне (ремнях),
N=(2ν 3600)Lh
–число циклов (перегибов) ремня за срок службы Lh час, m (= 8 для клиновых
ремней, = 5 для плоских ремней) – показатель кривой выносливости. Принимая за
142