Моменты сопротивления при изгибе и кручении (16.10) и (15.14) в формулах
(16.12)
W = 0,1d3 |
, |
W = 0,2d3 |
, |
u |
|
ρ |
|
суммарный изгибающий момент (рис. 16.5)
M =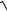 
M x2 +M у2.
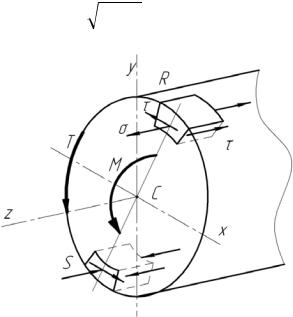
Рисунок 16.7 – Нормальные и касательные напряжения на поперечных и
продольных площадках в окрестностях опасных точек
На рисунке 16.7 показаны бесконечно малые элементы, содержащие опасные точки сечения, на их гранях нормальные и касательные напряжения, подчиненные закону парности (15.4). Две грани элементов свободны от напряжений. Напряженное состояние на рисунке 16.7 называется плоским.
Вдобавок, нормальные напряжения действуют только на двух гранях из шести. Этот частный случай плоского напряженного состояния называют упрощенным.
Лекция 17. Упрощенное плоское напряженное состояние (УПНС)
17.1 Напряженное состояние в точке
УПНС на рисунке 17.1 есть результат наложения (суперпозиции) чистого сдвига (ЧС) на рисунке 17.3 на линейное напряженное состояние (ЛНС) на рисунке 17.2. Первое имеем (рис. 15.3) при кручении круглого стержня, второе (рис.13.2) – при изгибе (и при растяжении-сжатии). Нормальные напряжения на рисунке 17.1 (растягивающие) считаем положительными, касательные напряжения, "вращающие" элемент по ходу часовой стрелки, – положительными; на "горизонтальных" площадках они отрицательные.
112
Рисунок 17.1 – УПНС: |
исходные |
напряжения, |
напряжения |
на |
|||
произвольной |
площадке; |
главные |
напряжения, |
||||
экстремальные касательные напряжения |
|
|
|
||||
Изучить напряженное состояние в точке – значит найти напряжения на любой площадке, проходящей через точку, или на любой площадке, проведенной внутри элемента, содержащего точку. Напряжения pα в УПНС, представленные
на рисунке 17.1 составляющими ραх, ρα у , найдем, суммируя такие же напряжения
на той же площадке в ЛНС и ЧС.
Отделим мысленно левую часть элемента, находящегося в равновесии, от правой. Силы на рисунке 17.2
dN =σdA, dPαx = pαxdAα |
(17.1) |
получены умножением напряжений на площади граней элемента, площадь наклонной грани
dA |
= |
dA |
. |
|
|
|
|||
α |
|
cosα |
|
|
|
|
|
||
Силы (17.1) уравновешены, следовательно: |
|
|||
dN = dPαx , |
|
|||
напряжения |
|
|
|
|
pαx |
=σ cosα. |
(17.2) |
||
Рисунок 17.2 – ЛНС
113
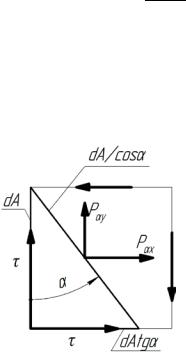
17.2 Чистый сдвиг
Силы, действующие на грани левой части элемента, равновесии,
dT =τdA, dT′ =τ (dA)tgα ;
dPαx = pαxdA / cosα, dPα у = pα у cosdAα .
Уравнения равновесия
dT = −dPα у, dT′ = −dPαх;
напряжения
ρα у = −τ cosα, ραх = −τ sinα .
Рисунок 17.3 – Чистый сдвиг
находящегося в
(17.3)
17.3 Нормальные и касательные напряжения в УПНС
Составляющие напряжения pα в УПНС найдутся суммированием составляющих (17.2) и (17.3):
pαх =σ cosα −τ sinα, |
(17.4) |
|
pα у = −τ cosα. |
||
|
Нормальные напряжения – проекция напряжений pα , или сумма проекций напряжений (17.4) на нормаль n к площадке; касательные напряжения – сумма
проекций напряжений (17.4) на ось t : |
|
|
σα = прn.pα = прn.pαх + прn.pα у =(σ cosα −τ sinα)cosα −τ cosαsinα; |
|
|
τα = прt .pα = прt .pαx − прt .pα у =(σ cosα −τ sinα)sinα +τ cosα cosα, |
|
|
или |
|
|
σα =σ cos2 α −τ sin 2α, |
(17.5) |
|
τα = 1σ sin 2α +τ cos2α. |
||
|
||
2 |
|
|
Введем в формулы (17.5) выражение |
|
|
114 |
|
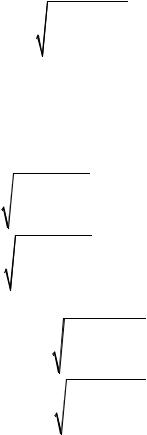
cos2 α =1+ cos2α , 2
и выразим напряжения (17.5) через функции двойного угла:
σα = σ |
+ |
σ cos2α −τ sin 2α, |
|
|
|||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
(17.6) |
τα = |
σ sin 2α +τ cos2α. |
|
|||||||||
|
|
||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
17.4 Максимумы и минимумы нормальных и касательных |
|||||||||||
напряжений в УПНС |
|
|
|
|
|
|
|
|
|
|
|
Функции |
|
|
|
|
|
|
|
|
|
|
|
ϕ (α)= σ cos2α −τ sin 2α, |
|
|
|||||||||
1 |
|
2 |
|
|
|
|
|
|
|
|
(17.7) |
|
|
|
|
|
|
|
|
|
|
||
ϕ2 (α)= |
σ sin 2α + cos2α, |
|
|||||||||
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
входящие в формулы (17.6), можно написать в виде |
|
||||||||||
ϕ (α)= A |
σ / 2 cos2α − τ sin 2α |
|
, |
||||||||
1 |
|
A |
|
|
|
A |
|
|
|
||
|
|
|
|
|
|
|
|
||||
ϕ2 (α)= A |
σ / 2 |
sin 2α + |
τ |
|
|
, |
|||||
|
A |
|
A |
cos2α |
|||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ 2 |
+τ |
2 |
. |
|
|
|
|
A = |
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
Коэффициенты при cos2α и sin 2α не превышают единицы, а сумма их квадратов равна единице; следовательно, можно положить
|
σ / 2 |
|
= cos β, |
τ =sin β, |
|||||||||||
|
A |
|
|
|
|
|
|
A |
|
|
|
|
|
||
что позволит написать: функции (17.7) |
|
|
|
|
|
|
|
||||||||
ϕ |
(α)= |
|
σ 2 |
+τ2 |
|
cos(2α + β), |
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
(17.8) |
||
|
|
|
|
σ 2 |
|
|
|
|
|
|
|
|
|
||
ϕ2 (α)= |
|
+τ |
2 |
|
sin(2α + β); |
||||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
максимумы и минимумы функций (17.8) |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ϕ1max |
= ± |
|
σ |
2 |
+τ |
2 |
, |
|
||||||
|
|
|
|
|
|
|
|||||||||
|
min |
|
|
2 |
|
|
|
|
|
(17.9) |
|||||
|
|
|
|
|
|
|
σ |
|
2 |
|
2 |
|
|||
|
ϕ2max |
= ± |
|
|
|
+τ |
. |
||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
min |
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
115 |
|
|
|
|
||
Введем максимумы и минимумы (17.9) в формулы (17.6) и найдем максимум и минимум нормальных напряжений (главные напряжения)
σmax = |
σ |
± |
σ |
2 |
2 |
(17.10) |
||
2 |
|
2 |
|
+τ |
|
|||
min |
|
|
|
|
|
|
||
и максимум и минимум касательных напряжений
τmax = ± |
σ |
2 |
+τ |
2 |
. |
(17.11) |
|
|
2 |
|
|
||||
min |
|
|
|
|
|
|
|
Максимумы и минимумы (17.9) имеют место при углах 2α , разнящихся на 180°, то есть на взаимно перпендикулярных площадках: главные площадки, где действуют напряжения (17.10), взаимно перпендикулярны; площадки, где действуют экстремальные напряжения (17.11), взаимно перпендикулярны.
Равные значения функций (17.8) имеют место при углах 2α , разнящихся на 90°: площадки с напряжениями (17.11) наклонены к площадкам с главными
напряжениями (17.10) под углами 45 (рис. 17.2).
Заметим: когда cos(2α + β) в первой из функций (17.8) делается максимальным или минимальным, sin(2α + β) во второй из функций делается равным нулю; когда sin(2α + β) становится максимальным или минимальным, cos(2α + β)= 0. Иными словами, на главных площадках касательных напряжений
нет; однако, на площадках с экстремальными касательными напряжениями нормальные напряжения (17.6) равны σ / 2.
17.5 Прочность при линейном напряженном состоянии и чистом
сдвиге
Максимум и минимум (17.10) нормальных напряжений в ЛНС (τ = 0)
σmax =σ, σmin = 0 |
(17.12) |
действуют на исходных поперечных и продольных площадках (рис. 17.2). Максимум и минимум (17.11) касательных напряжений в ЧС (σ = 0)
τmax =τ , τmin = −τ |
(17.13) |
действуют на исходных поперечных и продольных площадках (рис. 17.3). Именно этими обстоятельствами объясняется интерес к напряжениям в
поперечных сечениях стержня при растяжении (сжатии), изгибе и кручении. Соответствующие условия прочности (см. экстремумы (17.12–17.13))
σ |
max |
=σ ≤ σ |
, τ |
max |
=τ ≤ τ |
, |
(17.14) |
|
[ ] |
|
[ ] |
|
допускаемые напряжения
σ |
= |
|
σпред |
, |
τ |
= |
τпред |
. |
(17.15) |
[ ] |
|
|
[s] |
[ ] |
|
[s] |
|||
Предельные напряжения в определениях (17.15) связываются с наступлением текучести материала стержня, то есть
116