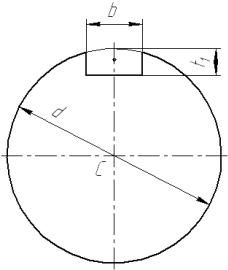
Вращающие моменты могут передаваться валу посредством шпонок, размещаемых в шпоночных пазах. Полярный момент инерции (15.8) сечения на рис. 15.5
I p = I pK − I pn ,
где I pK −полярный момент инерции круга (15.10); Iρп −полярный момент инерции
отрицательной площади сечения шпоночного паза, равный произведению этой площади на квадрат расстояния ее центра тяжести от центра С, то есть
I p = |
πd 4 |
d |
− |
t |
2 |
πd 4 |
− |
(вt1 )(d |
−t1 )2 |
(15.11) |
||
32 |
−(вt1 ) |
2 |
1 |
|
= |
32 |
4 |
. |
||||
|
|
|
2 |
|
|
|
|
|
||||
Рисунок 15.5 – К вычислению полярного момента инерции (15.11)
15.4 Моменты сопротивления при кручении
Наибольшие касательные напряжения (15.9) действуют (рис. 15.4) на периферии сечения:
τmax = |
T |
ρmax = |
T |
. |
(15.12) |
||||
|
|
||||||||
|
I p |
|
|
|
|
Wp |
|
||
Момент сопротивления сечения при кручении в формуле (15.12) |
|
||||||||
Wp = |
|
I p |
. |
|
|
(15.13) |
|||
|
|
|
|
||||||
|
|
|
|
ρmax |
|
|
|
||
Если сечения сплошные круговые, |
радиус ρmax = d / 2 и момент |
(15.13) (см. |
|||||||
полярный момент инерции (15.10)) |
|
|
|
|
|
|
|
||
Wp = πd 4 / 32 |
= |
πd3 |
≈ 0,2d3 . |
(15.14) |
|||||
d / 2 |
|
|
16 |
|
|
|
|||
Если сечение взято на участке со шпоночным пазом, радиус ρmax = d / 2 |
и момент |
|||||
(15.13) (см. формулу (15.11)) |
|
(вt1 )(d −t1 )2 |
|
|
||
Wp = |
πd3 |
− |
. |
(15.15) |
||
16 |
2d |
|||||
|
|
|
|
|||
|
|
|
104 |
|
|
|
15.5 Расчет на прочность
Выходные концы валов (с насаженными на них полумуфтами, шкивами, звездочками) работают на кручение. Условие прочности вала
τ |
max |
≤ τ |
] |
, |
|
|||
|
|
[ |
|
|
||||
или (см. наибольшее касательное напряжение (15.12)) |
|
|||||||
|
T |
|
≤[τ], |
(15.16) |
||||
Wp |
||||||||
|
|
|
|
|||||
где момент сопротивления круглого сечения дается формулой (15.14).
Из условия (15.16) находится требуемый диаметр выходного конца вала:
d ≥ 3 |
|
T |
|
|
, |
(15.17) |
|
0,2 |
|
τ |
] |
||||
|
|
|
[ |
|
|
||
допускаемое касательное напряжение [τ]= 20...25 МПа.
Найденный диаметр (15.17) и длина выходного участка вала согласуются с диаметром насадочного отверстия и длиной ступицы соединительной муфты (в курсовом проекте упругой втулочно-пальцевой МУВП или зубчатой МЗ), способной передать расчетный момент:
Тp = KT,
K – коэффициент режима работы привода, или же с длинами ступиц шкива, звездочки ременной, цепной передач.
Лекция 16. Напряженное состояние вала
16.1 Расчетная схема
На рисунке 16.1 показан быстроходный вал прямозубого редуктора в приводе, построенном по схеме ЭД →СМ → ЗП →ОП → П(см. лекцию 6). На
него действуют окружная и радиальная силы в зацеплении шестерни с колесом, сила кривошипного эффекта работающей муфты
Fм ≈125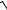
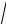ТБ
и момент, передаваемый полумуфтой.
Перенесем все силы на ось вала: радиальная сила Fr в зацеплении переносится вдоль линии действия, окружная сила Ft −параллельным переносом. Во втором случае наряду с силой Ft , приложенной в точке С на оси вала, "возникает" пара сил с моментом, уравновешивающим вращающий момент ТБ .
Действительно, момент "возникшей" пары, равный моменту переносимой силы Ft относительно новой точке приложения:
F d1 |
= |
2ТБ |
d1 |
=Т |
|
. |
|
|
|||||
t 2 |
|
d 2 |
|
Б |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
105 |
|
|
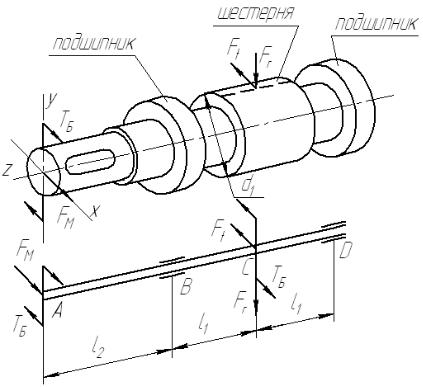
Рисунок 16.1 – Быстроходный вал редуктора и его расчетная схема
16.2 Опорные реакции
Силы, действующие на вал, воспринимаются подшипниками, передающими их корпусу редуктора. Со стороны корпуса действуют опорные реакции. Подшипники воспринимают их своими внешними кольцами и при посредстве тел качения (шариков или роликов) передают эти силы своим внутренним кольцам и, наконец, валу.
Представим все заданные силы на валу двумя системами сил – силами, действующими в вертикальной на рисунке плоскости YZ , и силами, действующими в горизонтальной плоскости XZ ; соответственно, и опорные реакции представляются своими вертикальными и горизонтальными составляющими.
На рисунке 16.2 показаны вертикальные силы. Единственная заданная сила Fr приложена в середине пролета ВD, опорные реакции, уравновешивающие
силу Fr , очевидно, равны по величине. Уравнение проекций ΣY = 0, или
Rву − Fr + RDу = 0,
дает |
|
|
1 F . |
|
R |
= R |
= |
(16.1) |
|
ву |
Dу |
|
2 r |
|
106
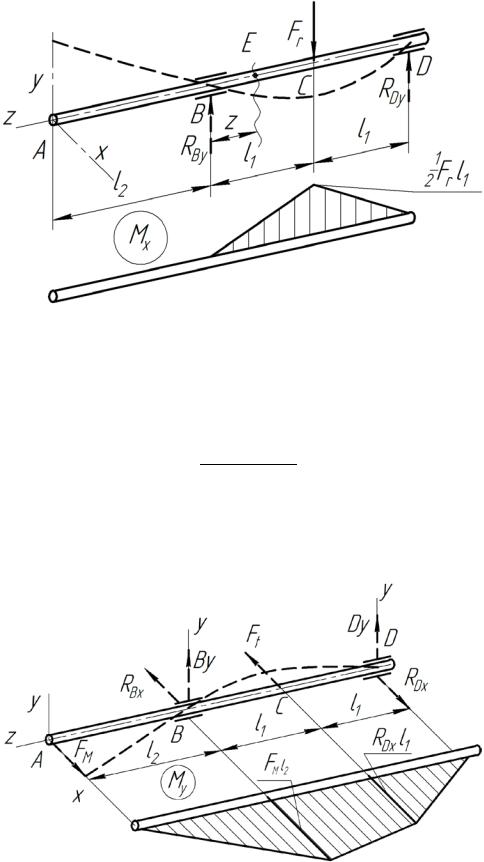
Рисунок 16.2 – Опорные реакции и изгибающие моменты в вертикальной
плоскости
На рисунке 16.3 показаны горизонтальные силы. Опорные реакции удобно найти из уравнений моментов:
ΣmBy = 0, −RDx 2l1 + Ft l1 + Fмl2 = 0,
RDx = Ft l1 +lFм l2 ;
2 1
ΣmDy = 0, Fм (l2 + 2l1 )− RBx 2l1 − Ftl1 = 0, |
(16.2) |
||
|
|||
R = |
Fм (l2 + 2l1 )− Ft l1 |
. |
|
|
|
||
Bx |
2l1 |
|
|
|
|
||
Рисунок 16.3 – Опорные реакции и изгибающие моменты в горизонтальной плоскости
107