
Элементарная математика / Ponarin-I
.pdf
Пусть CD — биссектриса треугольника ABC. На основании п. 2.4
AD = b и поэтому
DB a
|
|
|
|
|
|
|
|
|
= |
CA + (b/a)CB |
= |
|
aCA + bCB |
. |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
CD |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + b/a |
|
a + b |
||||||||||||||||||||||
Находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CD2 |
= |
|
(a2CA2 + 2ab(CA |
· CB) + b2CB2) = |
|||||||||||||||||||||||||||||||||
(a + b)2 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
(2a2b2 + 2ab(CA · CB)). |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a + b)2 |
||||||||||||||
По теореме косинусов 2 |
|
|
· |
|
|
= a2 + b2 − c2. Следовательно, |
|||||||||||||||||||||||||||||||
CA |
CB |
||||||||||||||||||||||||||||||||||||
lc2 = |
ab |
(2ab + a2 + b2 − c2) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
(a + b)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
= |
|
|
|
ab |
|
|
((a + b)2 |
− |
c2) = |
ab(a + b + c)(a + b − c) |
. |
|||||||||||||||||||||
|
|
|
|
|
(a + b)2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a + b)2 |
||||||||||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
l2 = |
ab(a + b + c)(a + b − c) |
(3.17) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
(a + b)2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4abp(p − c) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 = |
|
. |
|
|
|
(3.18) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
(a + b)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
З а д а ч а. Доказать, что если две биссектрисы треугольника равны, то он равнобедренный (теорема Ш т е й н е р а—Л е м у с а).
Эта задача была послана в 1840 году великому швейцарскому геометру Якобу Штейнеру С. Л. Лемусом с просьбой дать чисто геометрическое ее решение. Доказательство Штейнера было очень сложным и побудило других математиков искать более простое. Задача активно решалась более 20 лет. Некоторые математики обращались к решению этой задачи и в XX веке.
Алгебраическое решение по формуле (3.17) достаточно просто. Так как по условию la = lb, то
bc(a + b + c)(b + c − a) |
= |
ac(a + b + c)(c + a − b) |
, |
(b + c)2 |
|
(a + c)2 |
|
что эквивалентно равенству
b(a + c)2(b + c − a) = a(b + c)2(c + a − b).
31

Произведя умножение и надлежащую группировку слагаемых, получим:
(a3b − ab3) + 3abc(a − b) + c2(a2 − b2) + c3(a − b) = 0
и далее (a − b)(a2b + ab2 + ac2 + bc2 + c3 + 3abc) = 0.
Числа a, b и c положительны, поэтому сумма во вторых скобках положительна. Следовательно, a − b = 0, a = b.
Упражнения
3.1.Докажите, что для прямоугольного треугольника с катетами a
иb и гипотенузой с имеет место равенство:
r = 12 (a + b − c).
3.2.Докажите, что высота прямоугольного треугольника, опущенная на гипотенузу, равна сумме радиусов окружностей, вписанных в данный треугольник и в треугольники, на которые его делит эта высота.
3.3.Докажите, что площадь прямоугольного треугольника равна произведению длин отрезков, на которые делит его гипотенузу точка касания вписанной окружности.
3.4.Дан квадрат со стороной a. Через его центр, вершину и середину стороны, не содержащей эту вершину, проведена окружность. Найдите
еерадиус.
3.5.Если p и q — радиусы окружностей, проходящих через вершину A треугольника ABC и касающихся прямой BC в точках B и C, то pq = R2. Докажите.
3.6.Докажите, что для любого треугольника имеет место тождество:
a(sin B − sin C) + b(sin C − sin A) + c(sin A − sin B) = 0.
3.7.Если диагонали вписанного четырехугольника перпендикулярны, то сумма квадратов его противоположных сторон равна квадрату диаметра описанной окружности. Докажите.
3.8.Постройте треугольник по двум сторонам, если медиана, проведенная к третьей стороне, делит угол треугольника в отношении 1 : 2.
3.9.Через вершину A треугольника ABC внутри него проведены две прямые, образующие равные углы со сторонами AB и AC и пересекающие сторону BC в точках M и N. Докажите, что
BM · BN = AB2
CM CN AC2
(теорема Ш т е й н е р а).
32

3.10. Докажите, что расстояние между основаниями перпендикуляров, проведенных из какой-либо вершины вписанного в окружность четырехугольника к двум его сторонам, не зависит от выбора вершины.
Докажите следующие формулы площади треугольника (3.11—3.20).
3.11.S = 1 c2 sin A sin B . 2 sin C
3.12.S = 2R2 sin A sin B sin C.
3.13.S = 14 (a2 sin 2B + b2 sin 2A).
3.14.S = p2 tg A2 tg B2 tg C2 .
3.15.S = Rr(sin A + sin B + sin C).
3.16.S = 4Rr cos A2 cos B2 cos C2 .
3.17.S2 = abcp sin A2 sin B2 sin C2 .
p2
3.18. S = ctg(A/2) + ctg(B/2) + ctg(C/2) .
3.19. 4S2 = CA2 · CB2 − (CA · CB)2.
3.20. 16S2 = a2(b2 + c2 − a2) + b2(c2 + a2 − b2) + c2(a2 + b2 − c2).
3.21. Докажите, что в любом треугольнике ABC
r = 4R sin A2 sin B2 sin C2 .
3.22. На стороне AB треугольника ABC в одной полуплоскости с ним построен правильный треугольник ABC1. Докажите, что
CC12 = 12 (a2 + b2 + c2) − 2S√3,
где a, b и c — длины сторон треугольника ABC, S — его площадь. Докажите следующие соотношения для произвольного треугольника
ABC (3.23—3.25).
3.23.a2 = b2 + c2 − 4S ctg A.
3.24.a2 = (b + c)2 − 4S ctg A2 .
3.25.a2 = (b − c)2 + 4S tg A2 .
3.26.Углы треугольника ABC связаны условием:
cos2 A + cos2 B + cos2 C = 1.
Определите его вид.
3.27.Окружность радиуса R проходит через вершины A и B треугольника ABC и касается прямой AC в точке A. Найдите площадь треугольника ABC, если BAC = a и ABC = b.
3.28.Докажите, что в треугольнике ABC ортогональная проекция
биссектрисы CD на сторону CB имеет длину |
2p(p − c) |
. |
|
a + b |
|
33
3.29. В треугольник ABC вписана окружность радиуса r. Найдите длины сторон треугольника с вершинами в точках касания, если углы треугольника ABC равны a, b и g. Докажите, что площадь этого тре-
угольника равна pr2 .
2R
3.30. Докажите, что для любого треугольника выполняется соотношение:
a2 + b2 + c2 = 2p2 − 2r2 − 8Rr.
3.31. Найдите отношение произведения биссектрис острых углов прямоугольного треугольника к произведению радиусов его описанной
ивписанной окружностей.
§4. Четыре замечательные точки треугольника
Вгеометрии треугольника важную роль играют его четыре замечательные точки: точка пересечения медиан — центроид, центры вписанной и описанной окружностей, точка пересечения высот — ортоцентр. Рассмотрим подробнее их свойства.
4.1. Центроид треугольника. Его существование и основное свойство основано на следующей теореме о пересечении медиан треугольника.
Теорема. Три медианы треугольника пересекаются в одной точке G, которая делит каждую из них в отношении 2 : 1, считая от
|
|
|
|
вершины треугольника. |
|
|
|
|
C |
|
|
Из множества имеющихся доказательств |
|||
|
|
|
|
этой теоремы приведем четыре. |
|
||
|
|
|
|
Д о к а з а т е л ь с т в о 1. |
Пусть A1, |
B1 |
|
|
B1 |
A1 |
|
и C1 — середины сторон BC, CA и AB тре- |
|||
|
|
|
|
угольника ABC соответственно (рис. 25). |
|
||
|
G |
|
|
Пусть |
G — точка пересечения двух |
ме- |
|
|
P |
Q |
|
диан AA1 |
и BB1. Докажем сначала, |
что |
|
A |
C1 |
|
B |
||||
|
AG : GA1 = BG : GB1 = 2. |
|
|
||||
|
|
|
|
|
|
||
|
Рис. 25 |
|
|
Для этого возьмем середины P и Q отрез- |
|||
|
|
|
|
ков AG и BG. По теореме о средней линии |
|||
треугольника отрезки B1A1 и P Q равны половине стороны AB и па- |
|||||||
раллельны ей. Поэтому четырехугольник A1B1P Q — параллелограмм. |
|||||||
Тогда точка G пересечения его диагоналей P A1 и QB1 |
делит каждую |
||||||
из них пополам. Следовательно, точки P и G делят медиану AA1 на три |
|||||||
равные части, а точки Q и G делят медиану BB1 также на три равные |
|||||||
части. Итак, точка G пересечения двух медиан треугольника делит каж- |
|||||||
дую из них в отношении 2 : 1, считая от вершины. Докажем теперь, что |
|||||||
34
третья медиана CC1 содержит точку G. Согласно доказанному, точка |
|||
пересечения медиан AA1 и CC1 делит каждую из них в отношении 2 : 1. |
|||
На медиане AA1 такой точкой является точка G, поэтому она и будет |
|||
точкой пересечения прямых AA1 и CC1. Доказательство закончено. |
|||
|
Д о к а з а т е л ь с т в о 2 (векторное). Выберем произвольную точ- |
||
ку O в качестве общего начала векторов. На медиане AA1 возьмем точ- |
|||
ку G, делящую ее в отношении 2 : 1, считая от точки A (рис. 26). Тогда |
|||
|
O |
на основании формулы деления отрезка в данном |
|
|
отношении (п. 3.5) будем иметь: |
|
|
|
C |
|
|
|
A1 |
OA1 = 1 (OB + OC) и OG = OA + 2OA1 . |
|
|
G |
2 |
1 + 2 |
|
Отсюда |
|
|
A |
B |
|
|
|
Рис. 26 |
1 |
|
|
OG = 3 (OA + OB + OC). |
(4.1) |
|
|
|
||
В это выражение векторы OA, OB и OC вершин треугольника ABC |
|||
входят равноправно (симметрично). Поэтому векторы точек, делящих |
|||
другие две медианы в отношении 2 : 1, будут иметь то же выраже- |
|||
ние (4.1). Это и означает, что делящие точки совпадают. |
|
|
|
Следствие. Точка O совпадает с центроидом G треугольника ABC |
|||
тогда и только тогда, когда |
|
|
|
¯ |
|
|
|
OA + OB + OC = 0, |
|
|
|
иначе говоря, равенство |
|
|
|
¯ |
|
|
(4.2) |
GA + GB + GC = 0 |
|
|
|
есть характеристическое свойство центроида G треугольника ABC. |
|||
Третье доказательство теоремы о медианах треугольника основано |
|||
на таком характеристическом свойстве медианы тре- |
|
A |
|
угольника. |
|
|
|
|
|
|
|
Лемма. Для того, чтобы точка M принадлежа- |
|
|
|
ла прямой, содержащей медиану AA1 треугольника |
|
M |
|
ABC, необходимо и достаточно, чтобы треугольни- |
|
E |
|
ки AMB и AMC были равновелики и противополож- |
B |
A1 |
C |
но ориентированы. |
|
D |
|
Н е о б х о д и м о с т ь. Пусть A1 — середина сторо- |
|
Рис. 27 |
|
ны BC и M (AA1). Проведем высоты BE и CD в |
|
|
|
треугольниках AMB и AMC (рис. 27). Из равенства прямоугольных |
|||
треугольников BEA1 и CDA1 (по гипотенузе и острому углу) следу- |
|||
ет равенство BE = CD, которое влечет за собой равенство площадей |
|||
треугольников AMB и AMC. Они ориентированы противоположно. |
|||
35
Д о с т а т о ч н о с т ь. Пусть треугольники AMB и AMC равновелики и противоположно ориентированы. Тогда BE = CD. Если прямая AM пересекает прямую BC в точке A1, то A1 — середина стороны BC. Это следует из равенства тех же прямоугольных треугольников BEA1 и CDA1 (по катету и острому углу). Если бы AM была параллельна BC, то треугольники AMB и AMC были бы равновелики, но ориентированы одинаково, что противоречит условию.
Д о к а з а т е л ь с т в о 3 (теоремы о медианах). Пусть G — точка пересечения медиан AA1 и BB1. Тогда согласно лемме треугольники AGB и AGC равновелики, треугольники AGB и BGC также равновелики. Отсюда следует равновеликость треугольников AGC и BGC, которая по достаточному условию леммы эквивалентна тому, что G (CC1). Тремя медианами треугольник ABC разбился на шесть равновеликих треугольников. Поэтому
|
|
|
AG : GA1 = SAGC : SA1GC = 2. |
||
|
Аналогично BG : GB1 = 2 и CG : GC1 = 2. |
||||
|
Закончив это доказательство, сделаем одно замечание. В силу рав- |
||||
новеликости треугольников ABG, BCG и CAG точка G пересечения |
|||||
медиан треугольника ABC часто носит название центра тяжести |
|||||
этого треугольника, поскольку для материального треугольника, пред- |
|||||
ставляющего собой однородную пластинку, эта точка совпадает с фи- |
|||||
зическим центром тяжести. Однако если материальный треугольник |
|||||
|
|
C |
представляет собой совокупность трех однород- |
||
|
|
ных стержней, то его физический центр тяжести |
|||
|
|
|
|||
|
P |
M B1 |
уже не совпадает с точкой пересечения медиан, а |
||
|
A1 |
будет центром окружности, вписанной в середин- |
|||
|
Q |
|
ный треугольник A1B1C1. |
||
|
G |
|
Д о к а з а т е л ь с т в о 4 (методом параллель- |
||
B |
C1 |
A |
ного проектирования). Медиану CC1 разделим |
||
точками |
M и |
G на три равные части: CM = |
|||
|
Рис. 28 |
|
= MG = GC1, проведем прямую AG и параллель- |
||
|
|
|
ные ей прямые MP и C1Q, пересекающие сторону |
||
BC в точках A1, P и Q соответственно (рис.28). На основании теоремы |
|||||
Фалеса (п. 2.2) сторона BC разделилась точками Q, A1 и P на четыре |
|||||
равные части. Следовательно, A1 — середина BC. Аналогично прямая |
|||||
BG пересекает AC в ее середине B1. Так как P M — средняя линия тре- |
|||||
угольника A1GC и QC1 — средняя линия треугольника ABA1, |
|||||
|
|
|
AA1 = |
2QC1 = CC1 = 3, |
|
|
|
|
GA1 |
2P M |
CM |
откуда AG : GA1 = 2, и аналогично BG : GB1 = 2. |
|||||
|
|
|
|
36 |
|
4.2. Центр вписанной в треугольник окружности. Биссектрисы треугольника пересекаются в одной точке I, которая равноудалена от трех сторон треугольника и потому является центром вписанной в треугольник окружности. Доказательство имеется в школьных учебниках.
В каких отношениях делятся биссектрисы треугольника точкой I их пересечения? Решим эту задачу.
Пусть биссектрисы треугольника ABC пересекают его стороны AB,
BC и CA соответственно в точках C1, A1 и B1. Тогда BA1 : A1C = cb (п.2.4) и BA1 + A1C = a, откуда BA1 = bac+ c и A1C = bab+ c. Так как CI — биссектриса треугольника AA1C, то
|
|
|
|
AI |
= |
AC |
|
= b : |
ab |
|
= |
|
b + c |
. |
|
|
|
|||||
|
|
|
|
|
A1C |
b + c |
|
|
||||||||||||||
|
|
|
IA1 |
|
|
|
|
|
|
a |
|
|
|
|
|
|||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AI |
= |
b + c |
, |
|
BI |
|
= |
c + a |
, |
|
|
CI |
= |
a + b |
. |
(4.3) |
|||||
|
IA1 |
a |
|
|
|
|
|
|
IC1 |
|
||||||||||||
|
|
|
|
|
IB1 |
b |
|
|
|
|
c |
|
||||||||||
Далее, фиксируем некоторую точку O в качестве начала векторов (рис. 29) и выразим вектор OI центра вписанной окружности через векторы OA, OB, OC вершин треугольника и
Cдлины его сторон:
|
|
|
BA1 |
c |
|
|
bOB + cOC |
|
|
B1 |
A1 |
A1C |
= b |
|
OA1 = |
b + c |
, |
O |
|
|
|
|
OA + b + cOC |
|||
|
|
AI |
b + c |
|
|
|||
|
|
|
|
|
a |
|
||
|
|
|
IA1 = |
a |
OI = |
|
||
|
I |
|
1 + b + c . |
|||||
|
|
|
|
|
|
|
|
|
A |
C1 |
B |
|
|
|
|
a |
|
Итак, |
|
|
|
|
|
|||
|
Рис. 29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OI = a OA + b OB + c OC . |
(4.4) |
||||
|
|
|
|
|
|
a + b + c |
|
|
Следствие. Точка I является точкой пересечения биссектрис тогда и только тогда, когда
¯ |
(4.5) |
a IA + b IB + c IC = 0. |
4.3. Ортоцентр треугольника. Существование этой замечательной точки утверждается теоремой о пересечении высот треугольника.
Теорема. Прямые, содержащие высоты треугольника, пересекаются в одной точке (она называется ортоцентром треугольника).
Рассмотрим три доказательства этой теоремы.
37
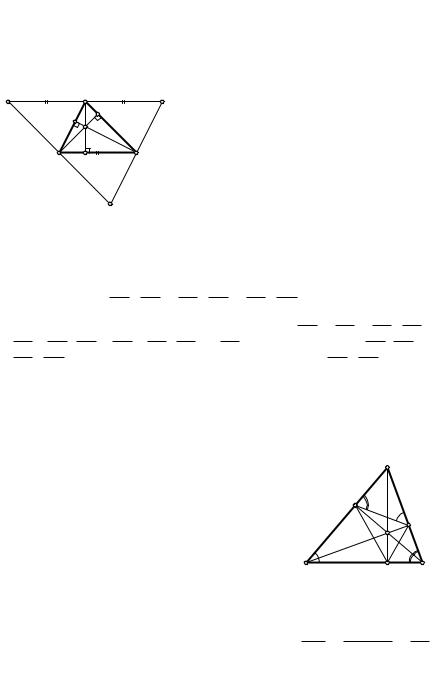
Д о к а з а т е л ь с т в о |
1. |
Через вершины треугольника ABC прове- |
|||
дем прямые, параллельные его противоположным сторонам. Тогда |
|||||
точки A, B и C будут серединами сторон полученного треуголь- |
|||||
ника |
A2B2C2 (рис. 30). Действительно, четырехугольники ABA2C и |
||||
ABCB2 — параллелограммы и поэтому CA2 = AB = CB2. Аналогично |
|||||
B2 |
C |
A2 |
точки |
A и B — середины отрезков B2C2 |
|
и C2A2 |
. Высоты AA1, BB1, CC1 треуголь- |
||||
|
A1 |
|
|||
|
|
ника ABC суть серединные перпендикуля- |
|||
|
B1 |
|
|||
Hры к сторонам треугольника A2B2C2. Они,
A |
|
B |
как известно, пересекаются в одной точ- |
||
C1 |
ке — центре окружности, описанной около |
||||
|
|
||||
|
|
|
треугольника A2B2C2. |
|
|
|
|
|
Следствие. Центр описанной |
около |
|
|
|
C2 |
треугольника окружности является ор- |
||
|
Рис. 30 |
|
тоцентром треугольника с вершинами в |
||
|
|
|
серединах сторон данного треугольника. |
||
Д о к а з а т е л ь с т в о 2 |
(векторное). Для любых четырех точек A, |
||||
B, C и D имеет место векторное тождество: |
|
||||
|
|
AB · CD + BC · AD + CA · BD = 0, |
(4.6) |
||
в чем легко убедиться, выполнив подстановки: CD = AD − AC, BC = |
|||||
= AC −AB, BD = AD −AB, CA = −AC. Если, в частности, BC ·AD = 0 |
|||||
иCA · BD = 0, то из тождества (4.6) следует, что и AB · CD = 0. Геометрически это означает, что если прямые BC и AD перпендикулярны
ипрямые CA и BD перпендикулярны, то перпендикулярны и прямые AB и CD. Иными словами, если точка D есть точка пересечения двух высот AA1 и BB1 треугольника ABC, то через нее проходит и третья высота CC1.
Ортоцентр треугольника ABC будем обо- |
|
C |
|
|
значать буквой H, если на то нет других ука- |
|
|
|
|
заний. |
|
|
B1 |
|
Очевидно замечательное свойство |
орто- |
|
|
|
|
|
A1 |
||
центра H непрямоугольного треугольника |
|
|
||
|
|
|
||
ABC: каждая из четырех точек A, B, C, H |
|
H |
|
|
является ортоцентром треугольника, обра- |
|
|
|
|
зованного тремя другими точками. |
A |
C1 |
B |
|
Д о к а з а т е л ь с т в о 3. Рассмотрим тре- |
|
Рис. 31 |
|
|
угольник A1B1C1 с вершинами в основаниях |
|
|
||
|
|
|
||
высот остроугольного треугольника ABC (рис. 31). Он называется ор- |
||||
тотреугольником треугольника ABC. Находим: |
CA1 = CA cos C |
= CA . |
||
|
|
CB1 |
CB cos C |
CB |
38 |
|
|
|
|
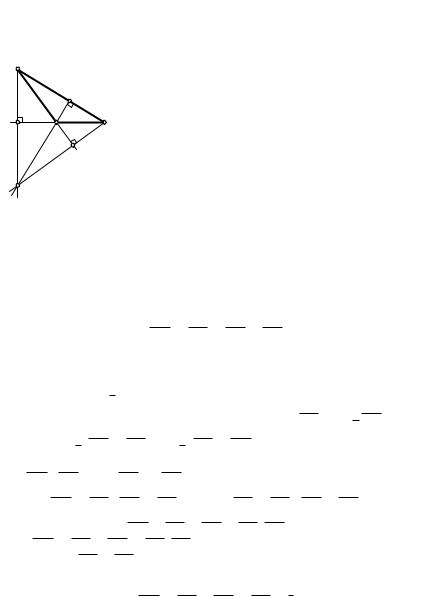
Поэтому 4A1B1C 4ABC, вследствие чего CA1B1 = BAC и, значит, |
||||
AA1B1 = 90◦ − A. Аналогично находим, что AA1C1 = 90◦ − A. Сле- |
||||
довательно, AA1 — биссектриса угла B1A1C1. На равных правах BB1 |
||||
|
C |
и CC1 — две |
другие биссектрисы |
треугольника |
|
A1B1C1. Итак, высоты остроугольного треуголь- |
|||
|
|
|||
|
A1 |
ника являются биссектрисами его ортотреуголь- |
||
|
никa. Они пересекаются в центре вписанной в него |
|||
|
|
|||
|
|
окружности. Теорема доказана для остроугольно- |
||
C1 |
A |
B го треугольника. Пусть теперь угол BAC тупой и |
||
|
B1 |
высоты BB1 |
и CC1 треугольника ABC пересека- |
|
|
ются в точке H (рис.32). Тогда углы треугольника |
|||
|
|
|||
H |
|
BCH острые (это непрямые углы прямоугольных |
||
|
|
треугольников) и CB1 и BC1 — его высоты, пе- |
||
|
Рис. 32 |
ресекающиеся в точке A. По доказанному третья |
||
|
|
высота проходит через A, т. е. HA BC. Доказа- |
||
|
|
тельство закончено. |
|
|
|
Следствие. Ортоцентр остроугольного треугольника служит цен- |
|||
тром окружности, вписанной в его ортотреугольник. |
|
|||
|
Теорема. Если O — центр окружности, описанной около треуголь- |
|||
ника ABC, H — его ортоцентр, то |
|
|||
|
|
OH = OA + OB + OC. |
(4.7) |
|
|
Д о к а з а т е л ь с т в о 1. Данный треугольник ABC гомотетичен его |
|||
серединному треугольнику A1B1C1 при гомотетии с центром G и коэф- |
||||
фициентом k = −21 . При этой гомотетии A → A1 и H → O (поскольку |
||||
O — ортоцентр треугольника A1B1C1). Поэтому OA1 = −21 HA, что эк- |
||||
вивалентно 21 (OB + OC) = −21 (OA − OH), откуда и следует (4.7). |
||||
|
Д о к а з а т е л ь с т в о 2. Для точек H и O запишем векторные усло- |
|||
вия AH · BC = 0 и OB2 = OC2. Представим их так: |
|
|||
|
(OH − OA)(OC − OB) = 0, |
(OC + OB)(OC − OB) = 0. |
||
Вычитая, получим: (OH − OA − OB − OC)BC = 0. Аналогичным обра- |
||||
зом (OH − OA − OB − OC)CA = 0. |
|
|||
|
Векторы BC и CA ненулевые и неколлинеарны. Поэтому последние |
|||
два равенства могут выполняться совместно лишь тогда, когда |
||||
OH − OA − OB − OC = 0.
4.4. Связь между четырьмя замечательными точками треугольника.
Если O — центр описанной около треугольника ABC окружности, то
39

равенства (4.1) и (4.7) выполняются совместно, а из них следует:
OH = 3OG.
Это значит, что точки O, G, H лежат на одной прямой, причем центроид G делит отрезок OH в отношении 1 : 2. Прямая, содержащая эти точки, называется п р я м о й Э й л е р а треугольника (рис. 33).
Расстояние между центрами O и I описанной и вписанной окружностей и радиусы R и r этих окружностей связаны замечательной формулой:
OI2 = R2 − 2Rr, |
(4.8) |
называемой ф о р м ул о й Э й л е р а. Вот два доказательства этой формулы.
P
C
C |
K |
|
|
|
|
|
O |
N |
|
|
M |
I |
|
|
|
|
GH |
|
A |
B |
O |
|
||
A |
B |
|
D |
Рис. 33 |
|
|
Рис. 34 |
Д о к а з а т е л ь с т в о |
1. |
Пусть биссектриса угла C треугольника |
|
ABC пересекает описанную около него окружность в точке D (рис.34). Проведем диаметр DP этой окружности и перпендикуляр IK из центра I вписанной окружности на сторону AC. Тогда IK = r, DP = 2R. Пусть прямая OI пересекает окружность в точках M и N. По теореме о секущих (п. 2.5)
CI · ID = IM · IN = (R + d)(R − d) = R2 − d2,
где d = OI. Это же произведение CI · ID вычислим иначе. Из подобия прямоугольных треугольников P AD и CKI (по равным острым
углам при вершинах P и C) имеем CI2R = ADr . Но AD = ID (задача 1.8). Поэтому CI · ID = 2Rr. Следовательно, R2 − d2 = 2Rr, что совпадает
с(4.8).
До к а з а т е л ь с т в о 2. Обращаясь к равенству (4.4), будем теперь полагать, что точка O — центр описанной окружности. Тогда находим
40
