
Элементарная математика / Ponarin-I
.pdf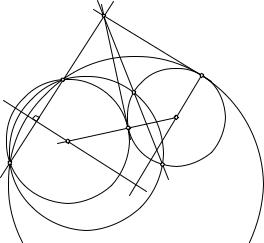
центров данного пучка, ортогональную a1 и a2 (рис. 132). Построим радикальную ось m окружности g и точки M. Она пересекает линию центров в центре X искомой окружности (критерий 1).
Единственность окружности пучка, содержащей данную точку M, доказывается рассуждением от противного. Пусть через M проходят две окружности x1 и x2 пучка, заданного окружностями a1 и a2. Тогда через точку M должны проходить все окружности пучка, что невозможно, поскольку M не принадлежит радикальной оси пучка.
З а д а ч а. Построить окружность, содержащую две данные точки A и B и касающуюся данной окружности a.
Р е ш е н и е. Искомая окружность x принадлежит эллиптическому пучку окружностей, пересекающихся в точках A и B. Пусть w — произвольная окружность этого пучка, пересекающая данную окружность a в точках M и N (рис. 133). Радикальные оси AB, MN и t окружностей a, w, x, взятых попарно, пересекаются в радикальном центре P , который можно построить, так как прямые AB и MN имеются. Далее строятся точки T и T1 касания с окружностью a прямых t и t1, проходящих через точку P , а по ним и центры X и X1 искомых окружностей. Исследование незатруднительно. Возможны 2, 1, 0 решений.
|
P |
|
|
t1 |
|
|
t |
|
A |
|
T1 |
|
|
|
|
M |
|
|
|
O |
X |
T |
x1 |
B |
N |
a |
|
|
 X1
X1
x
w
Рис. 133
Упражнения
131
17.1.Постройте окружность, касающуюся двух данных окружностей, при этом одной из них в данной точке.
17.2.Постройте окружность, проходящую через две данные точки A
иB и касающуюся данной прямой.
17.3.Постройте окружность, касающуюся данной окружности w и данной прямой в данной ее точке A.
17.4.Докажите, что два центра гомотетий двух окружностей являются концами диаметра окружности, которая принадлежит пучку окружностей, заданному двумя данными окружностями.
§18. Полярное соответствие
18.1.Поляра точки относительно окружности. Точки A и B называются сопряженными относительно окружности w(O, R), если
OA |
· |
OB |
= R2. |
(18.1) |
Из условия (18.1) непосредственно следует:
1)угол AOB либо острый, либо нулевой;
2)точка M сопряжена сама себе тогда и только тогда, когда она принадлежит базисной окружности w, так как
OM · OM = R2 M w;
3) центр O окружности w не имеет сопряженной ему точки, посколь-
¯ |
|
|
|
2 |
противоречиво; |
|
|
|
|
ку равенство 0 · OB = R |
|
w |
|
сопряженная |
|||||
4) если точка |
A = O |
лежит внутри окружности |
, то |
||||||
6 |
|
|
2 |
||||||
ей точка B лежит вне ее, так как из равенства OA · OB cos AOB = R |
|
||||||||
при OA < R следует OB > R.
Из равенства (18.1) легко также усматривается, что для заданной точки A, отличной от O, имеется бесконечное множество сопряженных с нею точек B, удовлетворяющих условию
w |
B |
|
|
|
f |
O A |
B0 |
Рис. 134
R2
OB cos f = OA = OB0,
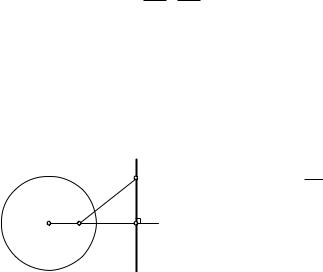
где OB и f = AOB переменные, а точка B0 — постоянная точка луча OA (рис. 134). Отрезок OB0 можно построить как четвертый пропорциональный к отрезкам R,
R, OA: OA : R = R : OB0. Точка B0 — единственная точка прямой OA, сопряженная с точкой A относительно w. Равенство
132
OB cos f = OB0 (f — острый угол!) говорит о том, что точка B0 является |
||||
ортогональной проекцией точки B на прямую OA. |
|
|
|
|
Следовательно, множеством всех точек, сопряженных с данной |
||||
точкой A относительно окружности w, является прямая BB0, пер- |
||||
пендикулярная к прямой OA. Она называется |
п о л я р о й |
точки A от- |
||
носительно данной окружности w. Точка A по отношению к своей по- |
||||
ляре называется полюсом этой прямой. |
|
|
|
|
Центр O окружности w не имеет поляры. Прямые, содержащие O, |
||||
не имеют полюсов. |
|
|
|
|
Существует несколько способов построения поляры данной точки A |
||||
относительно данной окружности w. Пока рассмотрим два из них. |
||||
Очевидно, достаточно построить лишь одну точку поляры a точ- |
||||
ки A — точку ее пересечения с прямой OA. С этой целью проведем |
||||
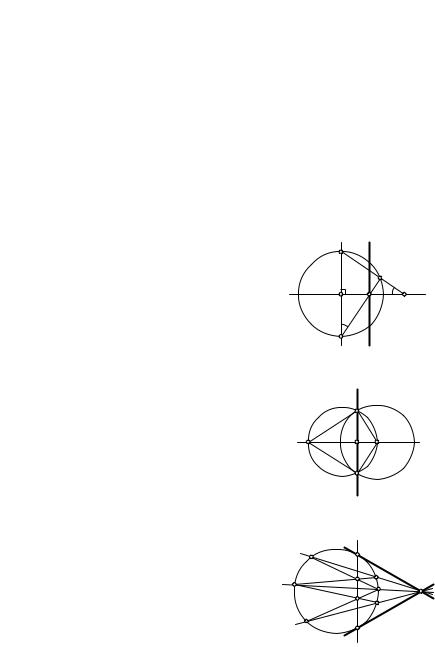
диаметр CD окружности w, перпендикулярный OA (рис. 135). Пусть |
||||
(AC) ∩ w = P , (P D) ∩ (OA) = B. Тогда точ- |
|
|
|
|
ка B — точка поляры a. Действительно, |
|
C |
|
|
из подобия прямоугольных треугольников |
w |
|
|
|
|
|
|
P |
|
AOC и BOD имеем OA/OC = OD/OB, т. е. |
|
|
|
|
|
O |
B |
A |
|
OA · OB = R2. Поляра a точки A проходит |
|
|||
через B перпендикулярно OA. |
|
|
|
|
Если точка A — точка окружности w, то |
|
|
|
|
ее полярой является касательная к w в этой |
|
D |
a |
|
точке, поскольку каждая точка окружности |
|
Рис. 135 |
|
|
сопряжена сама себе. |
|
|
||
|
|
|
|
|
Теорема. Если точка A лежит вне |
|
|
|
|
окружности w, то ее поляра содержит |
|
|
P |
w |
точки касания двух касательных, проведен- |
|
|
|
|
|
|
|
|
|
ных к w через точку A. |
A |
B |
|
O |
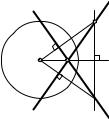
Действительно, если AP и AQ — каса- |
|
|
|
|
тельные к w и (P Q) ∩(AO) = B (рис.136), то |
|
|
|
|
из прямоугольного треугольника AOP име- |
|
Q a |
|
|
ем OA · OB = OP 2 = R2, т. е. точка B сопря- |
|
|
|
|
жена с A относительно w. |
|
Рис. 136 |
|
|
Следствие. Если точка A лежит вне |
|
|
p |
|
окружности w, то ее поляра a содержит |
|
w |
|
|
|
|
|
||
|
|
|
|
|
общую хорду окружности w и окружности |
|
|
|
|
с диаметром AO. |
|
|
|
P |
Другой способ построения поляры точки |
|
|
|
|
основан на утверждении задачи 2 § 9: точка |
|
|
|
|
пересечения диагоналей вписанного четы- |
|
|
|
|
рехугольника принадлежит поляре точки |
|
|
|
|
Рис. 137
133
пересечения его противоположных сторон.
Отсюда следует способ построения поляры
точки P одной линейкой. Через точку P проводим три секущие к базисной окружности w (рис. 137). Тогда поляра p точки P проходит через точки пересечения диагоналей полученных вписанных четырехугольников. Точки ее пересечения с окружностью суть точки касания двух касательных к окружности, проходящих через P . Поляра позволяет построить касательные к окружности одной линейкой.
Принцип построения поляры точки P остается тем же и в том случае, когда точка P лежит внутри базисной окружности w.
18.2. Свойство взаимности поляр. Поляры точек относительно окружности обладают замечательным свойством: если точка B лежит на поляре a точки A, то точка A лежит на поляре b точки B.
В самом деле, из того, что точка B лежит на поляре a точки A, следует, что точки A и B сопряжены относительно окружности w. Поэтому точка A лежит на поляре b точки B (рис. 138).
На основании этого свойства взаимности поляр поляра c точки C пересечения прямых a и b проходит через полюсы A и B этих прямых.
Из него же следует: поляры всех точек прямой проходят через полюс этой прямой.
w |
Отсюда очевиден способ построения полюса дан- |
|
bB ной прямой: надо на этой прямой взять две произ-
C |
c вольные точки, построить их поляры, тогда общая |
Oточка этих поляр и будет полюсом данной прямой.
18.3. Автополярный треугольник.. Построенный
 A выше треугольник ABC (рис. 138) обладает замечательным свойством: каждая его сторона является полярой противоположной вершины, каждая вершина есть полюс противолежащей стороны. Всякий
A выше треугольник ABC (рис. 138) обладает замечательным свойством: каждая его сторона является полярой противоположной вершины, каждая вершина есть полюс противолежащей стороны. Всякий
треугольник, обладающий этим свойством, называется автополярным треугольником относительно окружности w.
Центр O окружности w является ортоцентром автополярного относительно нее треугольника, так как по свойству поляры OA a, OB b,
OC c.
Автополярный треугольник ABC всегда тупоугольный, причем вершина тупого угла лежит внутри окружности w, а две другие вершины — вне ее.
В самом деле, точка и ее поляра всегда лежат в одной полуплоскости от прямой, проходящей через центр O окружности w параллельно этой поляре. Если бы точка O оказалась внутри треугольника ABC, то предыдущее условие не могло быть выполнено. Поэтому ортоцентр
134
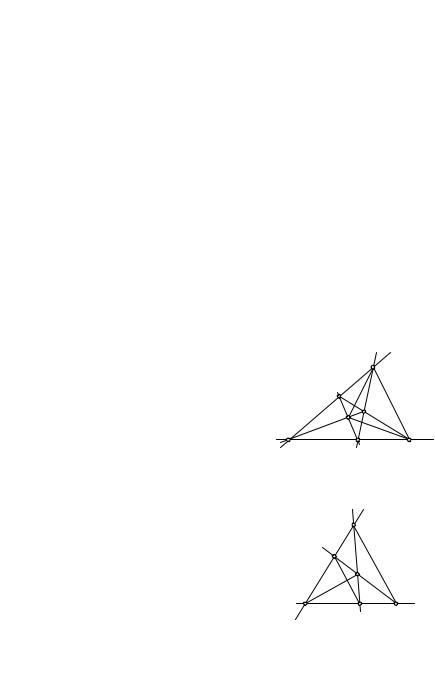
треугольника ABC лежит вне этого треугольника и, значит, он тупо- |
||||
угольный. |
|
|
|
|
Если точки A и B внешние относительно w, то их поляры a и b |
||||
пересекаются во внутренней относительно w точке C. Обратно, если |
||||
точка C внутренняя, то ее поляра состоит только из внешних точек |
||||
(п. 18.1, свойство 4). Таким образом, одна и только одна из вершин ав- |
||||
тополярного треугольника лежит внутри окружности w. Вершина C |
||||
автополярного треугольника ABC, внутренняя относительно w, лежит |
||||
внутри треугольника OAB и является его ортоцентром, поэтому тре- |
||||
угольник OAB остроугольный, а угол ACB тупой. |
|
|
|
|
18.4. Полярное соответствие относительно окружности. Принцип |
||||
двойственности. Если дана окружность с центром O, то между мно- |
||||
жеством точек плоскости (с исключенной точкой O) и множеством |
||||
прямых (кроме прямых, содержащих точку O) устанавливается вза- |
||||
имно однозначное соответствие: каждой точке соответствует ее поляра |
||||
и каждой прямой соответствует ее полюс. При этом множеству всех |
||||
точек прямой соответствует множество всех прямых пучка, и обратно. |
||||
Это соответствие называется полярным соответствием относительно |
||||
окружности. |
|
|
|
|
Полярное соответствие естественным образом приводит к принци- |
||||
пу двойственности в геометрии, который заключается в следующем. |
||||
Для любой конфигурации, состоящей из |
|
|
|
|
точек и прямых, в которой определенные |
|
|
P |
|
точки лежат на определенных прямых, су- |
|
|
|
|
|
|
|
|
|
ществует двойственная ей конфигурация |
|
D |
|
|
из прямых и точек, в которой определен- |
|
|
C |
|
ные прямые проходят через определенные |
|
|
|
|
|
|
M |
|
|
точки. |
|
|
|
|
|
|
B |
|
|
Например, фигуре, состоящей из четы- |
A |
|
N |
|
рех точек A, B, C, D, никакие три из ко- |
|
Рис. 139 |
|
|
торых не лежат на одной прямой, и шести |
|
|
|
|
прямых, соединяющих эти точки попарно |
|
|
|
|
(рис. 139), двойственна фигура, состоящая |
|
|
F |
|
из четырех прямых a, b, c, d, никакие три |
|
|
|
|
|
|
|
|
|
из которых не пересекаются в одной точ- |
|
C |
c |
|
ке, и шести точек, в которых попарно пе- |
|
|
|
|
b |
|
D |
|
|
ресекаются эти четыре прямые (рис. 140). |
|
|
||
|
|
|
||
|
|
d |
|
|
Первая фигура называется полным четы- |
|
|
|
|
|
|
|
|
|
рехвершинником (полным четырехуголь- |
B |
a |
A |
E |
ником), а вторая — полным четырехсто- |
|
Рис. 140 |
|
|
ронником. В полном четырехвершиннике |
|
|
||
135 |
|
|
|
|
ABCD прямые AB, BC, CD, DA, AC, BD
называются его сторонами, точки M = (AC) ∩ (BD), N = (AB) ∩ (CD), P = (BC) ∩ (AD) называются его диагональными точками, а прямые MN, MP , P N — его диагоналями.
В полном четырехстороннике abcd прямые a, b, c, d называются его сторонами, точки A = a ∩ d, B = a ∩ b, C = b ∩ c, D = c ∩ d, E = a ∩ c,
F= b ∩ d — вершинами, а прямые AC, BD, EF — диагоналями. Окружности w как множеству всех ее точек двойственна фигура,
представляющая собой множество всех касательных к w (поляр точек w). А это последнее множество прямых определяет ту же самую окружность w как кривую, касающуюся каждой прямой данного множества.
Каждой теореме о конфигурации прямых и точек соответствует двойственная теорема о двойственной конфигурации точек и прямых. Вторую (двойственную) теорему можно получить из первой взаимной заменой слов:
точка |
— прямая, |
полюс |
— поляра, |
лежит на |
— проходит через, |
коллинеарные точки |
— прямые, пересекающиеся в |
|
одной точке, |
трехвершинник (треугольник) |
— трехсторонник (треугольник), |
четырехвершинник |
— четырехсторонник, |
касательная |
— точка касания |
и т. д. Обе теоремы двойственны друг другу, т. е. одна из теорем верна если и только если верна вторая.
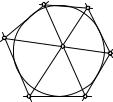
П р и м е р 1. Обратимся к теореме Паскаля (§ 10): точки пересечения противоположных сторон вписанного шестиугольника лежат на одной прямой. В полярном соответствии от-
|
B |
C |
носительно описанной около него окружности |
|
|
||
|
|
|
|
|
|
|
вершинам этого шестиугольника соответствуют |
A |
P |
|
касательные в этих вершинах. Следовательно, |
|
D |
вписанному шестиугольнику соответствует опи- |
|
|
|
||
|
|
|
санный шестисторонник (шестиугольник). Точ- |
|
|
|
кам пересечения противоположных сторон впи- |
F |
|
E |
санного шестиугольника соответствуют прямые, |
|
Рис. 141 |
|
соединяющие противоположные вершины опи- |
|
|
|
санного шестиугольника. Итак, теореме Паскаля |
будет двойственна теорема: в описанном шестиугольнике прямые, со-
136

единяющие его противоположные вершины (т.е. большие диагонали), пересекаются в одной точке (рис. 141).
Французский математик Шарль Б р и а н ш о н (1785—1864) доказал эту теорему в 1806 г., поэтому она носит его имя — теорема Брианшона. Простых прямых доказательств ее не имеется.
П р и м е р 2. В описанном четырехугольнике прямая, содержащая точки касания двух смежных сторон, и прямая, содержащая точки касания двух остальных сторон, пересекаются на продолжении диагонали этого четырехугольника (рис. 142). Этому предложению двойственно предложение: во вписанном четырехугольнике точка пересечения касательных в двух смежных вершинах и точка пересечения касательных в двух оставшихся вершинах лежат на одной прямой с точкой пересечения двух противоположных сторон (рис. 143). Наблюдательный читатель без труда заметит, что в этих двух разных на первый взгляд предложениях по существу содержится один и тот же факт. Доказательству подлежит только одно из этих предложений. Проще доказывается первое. Сделайте это в качестве несложного упражнения.
Рис. 142 |
Рис. 143 |
П р и м е р 3. Пусть A и B — две произвольные точки, a и b — их поляры относительно окружности с центром O, AOB = f. Тогда угол между прямыми a и b, в котором лежит точка O, равен 180◦ − f. Следствием этого факта является взаимная двойственность двух утверждений: 1) во вписанном четырехугольнике сумма противоположных углов равна 180◦, 2) если O — центр окружности, вписанной в четырехугольник ABCD, то
AOB + COD = BOC + AOD = 180◦.
Упражнения
18.1. Докажите, что диаметрально противоположные точки одной окружности только тогда сопряжены относительно другой, когда эти окружности ортогональны.
137

18.2. Точка M — середина стороны AB треугольника ABC, H — его ортоцентр. Докажите, что
MC · MH = 14 AB2.
18.3.Точки A и B сопряжены относительно окружности тогда и только тогда, когда квадрат расстояния между ними равен сумме их степеней относительно этой окружности. Докажите.
18.4.Четырехугольник вписан в окружность. Докажите, что треугольник с вершинами в точках пересечения его противоположных сторон и точке пересечения диагоналей является автополярным относительно этой окружности.
18.5.Точки A и A1, B и B1 сопряжены относительно окружности w. Докажите, что точки C = (AB) ∩ (A1B1) и C1 = (AB1) ∩ (A1B) также сопряжены относительно w. Докажите, что окружности с диаметра-
ми AA1, BB1, CC1 принадлежат одному пучку.
18.6.Дан тупоугольный треугольник. Докажите, что существует единственная окружность, относительно которой этот треугольник является автополярным. Постройте эту окружность.
18.7.Даны три окружности, центры которых не лежат на одной прямой. Найдите множество точек, для каждой из которых три сопряженные ей точки относительно данных окружностей совпадают.
18.8.Дана окружность и на ней точка A. С помощью одной линейки постройте касательную к окружности в точке A.
18.9.Дан прямоугольник с центром в центре O окружности w. Докажите, что его образом в полярном соответствии относительно w является ромб.
18.10.Постройте конфигурацию, двойственную конфигурации Паппа (упр. 10.9). Сформулируйте теорему, двойственную теореме Паппа.
18.11.Сформулируйте теорему, двойственную теореме Брианшона для описанного четырехугольника (упр. 10.11).
Задачи общего содержания
1.Стороны параллелограмма равны a и b, а угол между диагоналями равен a. Найдите площадь параллелограмма.
2.Площадь ромба равна S, сумма длин его диагоналей равна m. Найдите длину стороны ромба.
3.Высота и биссектриса прямоугольного треугольника, проведенные через вершину прямого угла, равны соответственно 3 и 4. Найдите площадь треугольника.
138

√ √
4. Дана трапеция ABCD с основаниями AD = 3 39 и BC = 39,BAD = 30◦, ADC = 60◦. Через точку D проведена прямая, делящая трапецию на равновеликие части. Найдите длину отрезка этой прямой, находящегося внутри трапеции.
5.Найдите сторону квадрата, вписанного в прямоугольный треугольник с катетами 3 и 4. Одна сторона квадрата принадлежит гипотенузе.
6.В треугольнике ABC биссектриса AK перпендикулярна медиане BM, угол ABC равен 120◦. Найдите отношение площади треугольника ABC к площади описанного около него круга.
7.Даны углы a, b, g треугольника ABC и медиана AM = m. Вычис-
лите его площадь. |
√7. Диагонали |
8. В трапеции ABCD длина основания AD равна |
ее пересекаются в точке K, AK = 1, KD = 2, BAC = DAC. Найдите площадь треугольника ABC.
9.Угол при основании равнобедренного треугольника равен a. В каком отношении делит площадь этого треугольника прямая, делящая его основание в отношении 2 : 1 и составляющая острый угол b с меньшей частью основания?
10.Прямая AD делит медиану BM треугольника ABC в отношении 5 : 1, считая от точки B. В каком отношении эта прямая делит площадь треугольника ABC?
11.На сторонах AB, BC, CD, DA выпуклого четырехугольника ABCD взяты соответственно точки K, L, M, N, делящие их соответственно в отношениях 2 : 1, 1 : 3, 1 : 1, 1 : 5. Площадь четырехугольника ABCD равна 1. Найдите площадь шестиугольника AKLCMN.
12.Найдите площадь трапеции с основаниями a и b (a > b), у которой диагонали перпендикулярны, а угол между боковыми сторонами равен a.
13.В прямоугольной трапеции ABCD меньшее основание AD равно a, боковая сторона CD, не перпендикулярная к основаниям, равна 2a. Точка E — середина CD, угол CBE равен a. Найдите площадь данной трапеции.
14.Вычислите площадь трапеции, если даны длины e и f ее диагоналей и длина m отрезка, соединяющего середины ее оснований.
15.Через вершину C прямого угла треугольника ABC проведена прямая l, перпендикулярная медиане CM треугольника ABC. Точки A1
иB1 — ортогональные проекции вершин A и B на прямую l. Докажите, что
1) площадь трапеции AA1B1B вдвое больше площади треугольника
ABC,
139
2) 4AA1 · BB1 = A1B12.
16.В равнобедренном треугольнике основание и боковая сторона равны соответственно 6 и 5. Найдите расстояние между центрами вписанной и описанной окружностей.
17.Точка D лежит на стороне AC правильного треугольника ABC. Найдите отношение радиусов окружностей, описанных около треугольников ABD и ABC, если AD : AC = n.
18.Две окружности касаются внутренним образом. Прямая, проходящая через центр меньшей окружности, пересекает большую окружность
вточках A и D, а меньшую — в точках B и C. Найдите отношение радиусов окружностей, если AB : BC : CD = 2 : 4 : 3.
19.Окружность, вписанная в треугольник ABC, делит медиану BM на три равных отрезка. Найдите отношение сторон треугольника.
20.В прямоугольном треугольнике длины катетов равны a и b (a<b). Найдите радиус окружности, проходящей через середину меньшего катета и касающейся гипотенузы в ее середине.
21.В прямоугольном треугольнике ABC проведена высота CD на гипотенузу AB. Найдите расстояние между центрами окружностей, вписанных в треугольники BDC и ADC, если BC = 4, AC = 3.
22.Вписанная в треугольник ABC окружность касается стороны BC в точке D, а вневписанная окружность касается стороны BC в точке E. Найдите длину DE, если радиусы этих окружностей равны 3 и 4, а угол BCA равен 120◦.
23. Трапеция ABCD с основаниями BC = 2 и AD = 10 такова, что в нее можно вписать окружность и около нее можно описать окружность. Определите положение центра описанной окружности относительно трапеции. Найдите отношение радиусов этих окружностей.
24. Точка E лежит на стороне AC правильного треугольника ABC, точка K — середина отрезка AE. Прямая, проходящая через точку E перпендикулярно AB, и прямая, проходящая через точку C перпендикулярно AB, и прямая, проходящая через точку C перпендикулярно BC, пересекаются в точке D. Найдите углы треугольника BKD.
25. Равнобедренные треугольники ABC (AB = BC) и A1B1C1 (A1B1 = B1C1) равны. Точки A1, B1, C1 лежат соответственно на лучах BC, BA, AC вне данного треугольника ABC. Стороны B1C1 и BC перпендикулярны. Найдите углы треугольника ABC.
26. Окружность с центром на гипотенузе AB прямоугольного треугольника ABC пересекает гипотенузу в точках N и L, касается катета AC в точке M и касается катета BC. Найдите AB, если MN : AN = 1/6
и AM = 10/27.
140
