
Элементарная математика / Ponarin-I
.pdf
Д о к а з а т е л ь с т в о. Пусть M и M0 — произвольный и правильный n-угольники, описанные около данной окружности w. Опишем около M0 окружность и рассмотрим круг K, для которого эта окружность является границей. Площадь многоугольника M0 равна разности SK − − (c1 + c2 + . . . + cn) между площадью SK круга K и суммой площадей ci (i = 1, 2, . . . , n) сегментов этого круга, отсекаемых сторонами
многоугольника M0 |
(рис. 113). Важно заметить, |
|
что стороны многоугольника M отсекают от кру- |
|
|
га K сегменты, равные тем, которые отсекаются |
|
|
сторонами многоугольника M0, но в отличие от |
|
|
первых они могут |
иметь непустые пересечения. |
w |
Поэтому площадь c, занимаемая объединением |
|
|
вторых сегментов, будет меньше c1 + c2 + . . . + cn |
|
|
(за счет наложений и непустых пересечений). |
|
|
Пусть K ∩ M = F |
(заштриховано на рис. 113). |
|
Имеем: |
|
Рис. 113 |
SM >SF = SK − c > SK − (c1 + c2 + . . . + cn) = SM0 .
Так как площадь S и периметр 2p многоугольника M, описанного около окружности w радиуса r, связаны зависимостью S = pr, то при заданном r наименьшие значения S и p достигаются одновременно, т. е. по доказанному выше для правильного n-угольника.
З а д а ч а. Пусть R1, R2, R3 — расстояния от точки M до вершин треугольника ABC. Доказать, что
p√
R1 + R2 + R3 > 2 3S > 6r, (15.2)
где r — радиус вписанной в треугольник ABC окружности.
Р е ш е н и е. Построим точки, симметричные точке M относительно сторон треугольника ABC. Соединив их последовательно с вершинами данного треугольника, получим шестиугольник с площадью 2S и периметром 2(R1 + R2 + R3). Используем изопериметрическое неравенство
(15.1) при n = 6: |
2S 6 61 (R1 + R2 + R3)2 · √3, |
||
откуда |
|||
|
R1 + R2 + R3 > 2p√3S. |
||
√ |
2 |
||
Так как S > 27r |
|
(13.31), то |
|
R1 + R2 + R3 > 6r.
Равенство достигается только для правильного треугольника и его центра.
121
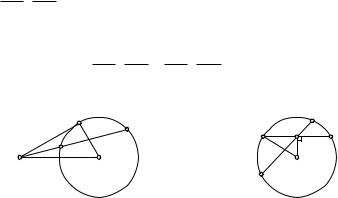
§16. Радикальная ось и радикальный центр окружностей
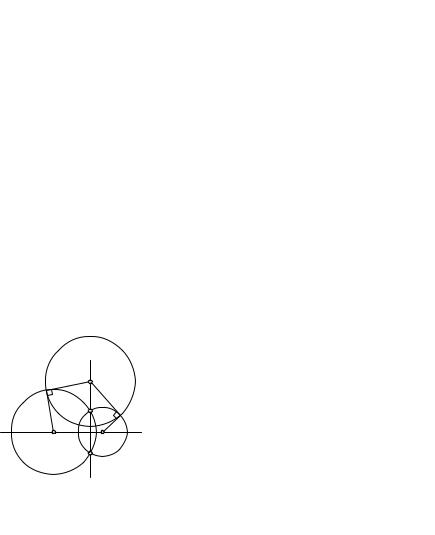
16.1.Степень точки относительно окружности. Возвратимся к теореме о хордах и секущих (§ 2). Пусть через внешнюю относительно окружности w(O, R) точку M проведена произвольная секущая, пересекающая эту окружность в точках A и B (рис.114), и касательная MT . Тогда MA ·MB = MT 2 = OM2 −R2. Эта величина не зависит от выбора секущей, а зависит от выбора точки M.
Если точка M лежит внутри окружности w, то проведем через нее две хорды — произвольную хорду AB и хорду CD, перпендикулярную
OM (рис.115). Тогда MA ·MB = MC ·MD = −MC2 = −(OC2 −OM2) =
=OM2 − R2. Наконец, в случае, когда M w, очевидно, OM2 − R2 = 0.
|
T |
B |
|
B |
|
|
|
C |
M |
D |
|
|
|
|
|||
|
A |
|
|
|
|
M |
|
O |
|
O |
|
|
|
w |
A |
|
w |
|
|
|
|
|
|
|
Рис. 114 |
|
|
Рис. 115 |
|
Итак, величина OM2 − R2 при заданной окружности w(O, R) зависит только от положения точки M. Она называется степенью точки M относительно окружности w. Степени точек, лежащих вне окружности w, положительны. Степени точек, лежащих внутри окружности w, отрицательны. Степени точек окружности w равны нулю.
16.2. Радикальная ось двух окружностей определяется как множество точек плоскости, каждая из которых имеет равные степени относительно этих окружностей.
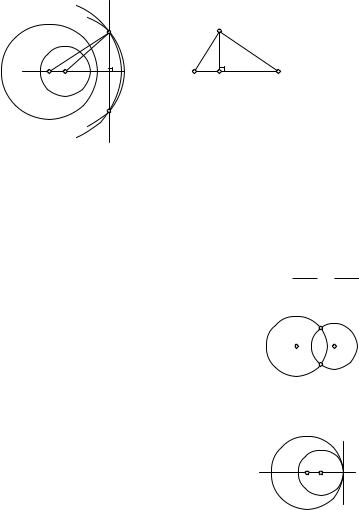
Теорема. Если две данные окружности (O1, R1) и (O2, R2) неконцентрические, то их радикальная ось существует и является прямой линией.
Д о к а з а т е л ь с т в о. Пусть точка M имеет равные степени относительно данных окружностей: O1M2 − R12 = O2M2 − R22, откуда O1M2 − −O2M2 = R12 −R22. Для определенности полагаем R1 >R2. Если R1 = R2, то O1M = O2M и поэтому искомое множество точек M есть серединный перпендикуляр к отрезку O1O2. При R1 > R2 построим отрезок a, для которого R12 − R22 = a2, и построим произвольный прямоугольный треугольник ABC с катетом BC = a, но такой, чтобы AB + AC > O1O2 (рис. 116, б). Тогда окружности (O1, AB) и (O2, AC) пересекаются и их
122
общие точки M и N принадлежат искомому множеству. Действительно,
O1M2 − O2M2 = AB2 − AC2 = BC2 = a2 = R12 − R22.
MB
|
R1 |
a |
|
|
|
|
|
O1 O2 |
R2 C |
A |
|
|
N |
|
|
а) |
|
б) |
|
|
Рис. 116 |
|
|
Итак, искомое множество точек непусто. Докажем теперь, что это множество точек есть прямая линия, перпендикулярная линии O1O2 центров данных окружностей. Пусть M — фиксированная точка, а X — произвольная точка этого множества. Тогда O1M2 − O2M2 = O1X2 −
−O2X2 и поэтому O1M2 + O2X2 −O1X2 −O2M2 = 0. С другой стороны, согласно формуле (11.2) O1M2 + O2X2 − O1X2 − O2M2 = 2O1O2 · XM.
|
|
|
|
|
|
|
|
|
|
|
Следовательно, O1O2 ·XM = 0 и O1O2 XM для |
|
|
||||||||
любой точки X радикальной оси. Поскольку точ- |
|
|
||||||||
|
|
|||||||||
ка M фиксирована, то радикальная ось двух окруж- |
|
|
||||||||
ностей |
есть прямая, |
проходящая |
через M пер- |
|
|
|||||
O1 |
O2 |
|||||||||
пендикулярно линии центров данных окружностей |
||||||||||
|
|
|||||||||
(рис. 116, а). Построение точки M уже рассмотрено. |
|
|
||||||||
|
|
|||||||||
Если |
данные |
окружности |
пересекаются |
Рис. 117 |
||||||
(рис. 117), то точки пересечения имеют равные (нулевые) степени относительно этих окружностей. Следовательно, их радикальная ось — прямая, содержащая эти точки.
Если данные окружности касаются внешним или внутренним образом, то их радикальная ось совпадает с общей касательной в точке касания окружностей (рис. 118).
Если окружности лежат одна вне другой, не ка-
саясь, то середина M их общей касательной имеет равные степени относительно их и потому принадлежит радикальной оси (рис. 119).
123
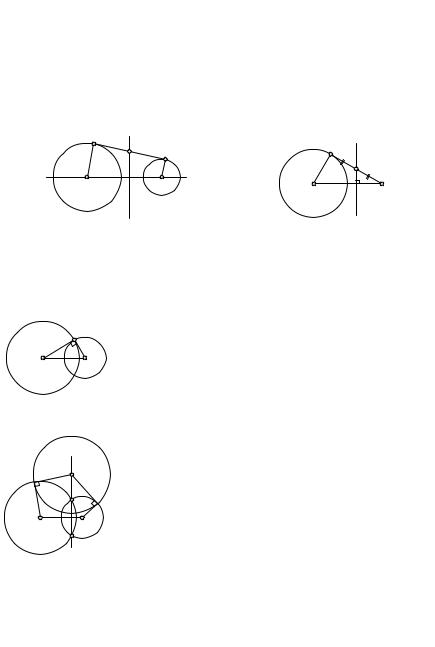
Понятие радикальной оси двух окружностей остается в силе и в |
||||||
том случае, когда одна из них вырождается в точку — «нулевую окруж- |
||||||
ность». При R2 = 0 степень точки M относительно такой окружности |
||||||
будет равна O2M2. Поэтому радикальная ось окружности (O1, R1) и |
||||||
точки O2 есть множество точек, степень каждой из которых относи- |
||||||
тельно этой окружности равна квадрату расстояния ее до точки O2 |
||||||
(рис. 120). |
|
|
|
|
|
|
|
|
M |
|
|
T |
|
|
|
|
|
|
||
|
|
|
|
|
M |
|
|
O1 |
O2 |
|
O1 |
O2 |
|
|
|
|
|
|||
|
|
Рис. 119 |
|
Рис. 120 |
||
16.3. Характеристические свойства точек радикальной оси окружно- |
||||||
стей. Кроме свойства точек радикальной оси, через которое она опре- |
||||||
|
|
делена, точки этой оси имеют еще другие замеча- |
||||
|
T |
тельные свойства, используемые при решении кон- |
||||
|
структивных задач. |
|
|
|||
|
|
|
|
|||
O1 |
O2 |
Напомним |
сначала |
понятие |
ортогональных |
|
окружностей. Две пересекающиеся окружности на- |
||||||
|
|
|||||
|
|
зываются ортогональными, если касательные к |
||||
Рис. 121 |
ним в их общей точке перпендикулярны (рис. 121). |
|||||
Центр каждой из двух ортогональных окружно- |
||||||
|
|
|||||
|
|
стей лежит на касательной к другой в их общей |
||||
|
|
точке. |
1◦. Внешние относительно каж- |
|||
r |
A |
С в о й с т в о |
||||
|
r |
дой из двух данных окружностей точки их ра- |
||||
|
|
дикальной оси являются центрами окружностей, |
||||
O1 |
O2 |
каждая из которых ортогональна обеим данным |
||||
окружностям. Обратно, если окружность ор- |
||||||
|
|
|||||
|
l |
a2 |
|
|
|
|
a1 |
тогональна двум данным окружностям, то ее |
|||||
|
||||||
Рис. 122 |
центр принадлежит их радикальной оси. |
|||||
В самом деле, если точка A принадлежит ра- |
||||||
|
|
|||||
|
|
дикальной оси l окружностей a1 и a2 и лежит вне |
||||
|
|
этих окружностей, то касательные, проведенные из |
||||
точки A к этим окружностям, имеют равные длины r (рис. 122). Тогда |
||||||
окружность (A, r) ортогональна каждой из данных окружностей. |
||||||
124
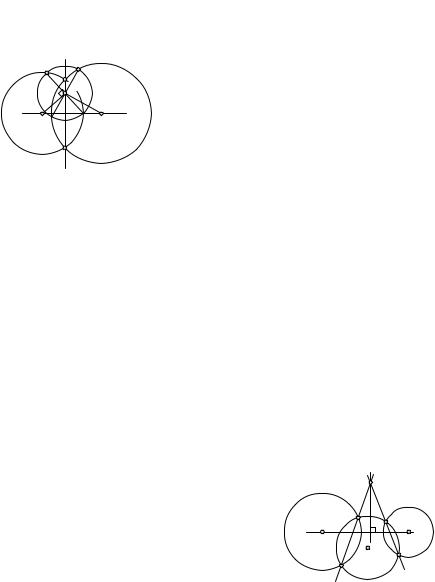
Обратно, если окружность (A, r) ортогональна каждой из окружно- |
||||
стей a1 и a2, то ее центр A есть точка пересечения касательных к этим |
||||
окружностям в их точках пересечения с окружностью (A, r). Тогда эти |
||||
|
|
|
касательные имеют равные длины, поэтому |
|
|
Ar |
|
точка A имеет равные степени относительно |
|
r |
|
окружностей и, следовательно, лежит на их |
||
|
|
|
радикальной оси. |
2◦. Внутренние относи- |
O1 |
O2 |
|
С в о й с т в о |
|
a1 |
|
a2 |
тельно каждой из двух данных окружно- |
|
|
|
стей точки их |
радикальной оси являют- |
|
|
|
|
||
lся центрами окружностей, каждая из ко-
торых делится пополам обеими данными окружностями. Обратно, если две данные окружности делят пополам третью окружность, то ее центр ле-
жит на радикальной оси этих окружностей.
Действительно, пусть точка A принадлежит радикальной оси l окружностей a1 и a2 и лежит внутри каждой из них (рис. 123). Равенство степеней точки A относительно окружностей означает равенство полухорд этих окружностей, содержащих точку A и перпендикулярных соответственно O1A и O2A (п.16.1). Поэтому окружность (A, r), где r — длина указанных полухорд, делится пополам каждой из окружностей a1
иa2. Доказательство обратного утверждения также просто.
16.4.Радикальный центр трех окружностей. Это понятие основано на следующей теореме.
Теорема. Если центры трех окружностей неколлинеарны, то три радикальные оси этих окружностей, взятых попарно, имеют общую точку.
В самом деле, пусть радикальная ось a окружностей a и g и радикальная ось b окружностей b и g пересекаются в точке P (рис. 124). Тогда точка P имеет равные степени отно-
сительно каждой из трех окружностей a, |
a |
P |
|||
b, g. Поэтому она лежит на радикальной оси |
b |
||||
|
|
||||
окружностей a и b. |
|
|
A |
B |
|
О п р е д е л е н и е. Общая |
точка |
ради- |
|||
|
|
||||
кальных осей трех окружностей, взятых по- |
C |
b |
|||
парно, называется радикальным центром |
|||||
a |
g |
||||
этих окружностей. |
|
|
|
||
|
|
|
|
||
Построение радикальной |
оси |
двух |
Рис. 124 |
||
окружностей рассмотрено в п. 16.2 вместе с доказательством теоремы о радикальной оси. Введение понятия ра-
дикального центра трех окружностей позволяет значительно упростить
125
построение радикальной оси в случае, когда эти окружности не пересекаются, что выполнено на рис. 124 для окружностей a и b. Этот способ остается в силе и в случае, когда одна из окружностей a и b лежит внутри другой.
Упражнения
16.1.Постройте окружность, ортогональную к трем данным окруж-
ностям.
16.2.На данной окружности найдите точку, чтобы касательные из нее к другой данной окружности были равны отрезку от искомой точки до данной точки A.
16.3.Постройте окружность, касательные к которой, проведенные из данных точек A, B, C, были бы равны соответственно трем данным отрезкам a, b, c.
16.4.Постройте окружность, проходящую через две данные точки A
иB и ортогональную данной окружности a.
16.5.Постройте окружность данного радиуса, ортогональную двум данным окружностям.
16.6.Через две данные точки A и B проведите окружность, делящуюся данной окружностью a пополам.
16.7.Через две данные точки A и B проведите окружность, которая делила бы данную окружность пополам.
16.8.Постройте окружность, которая делилась бы пополам каждой из трех данных окружностей. При каких условиях она существует?
16.9.На сторонах BC, CA, AB остроугольного треугольника ABC взяты соответственно три произвольные точки A1, B1, C1. Докажите, что три общие хорды пар окружностей с диаметрами AA1, BB1, CC1 пересекаются в ортоцентре треугольника ABC.
§17. Пучки окружностей
17.1.Определение пучка окружностей. Виды пучков. Предварительно убедимся в истинности такого утверждения.
Если прямая l является радикальной осью окружностей a и b и является радикальной осью окружностей b и g, то она есть также
ирадикальная ось окружностей a и g и центры этих трех окружностей коллинеарны.
Действительно, по определению радикальной оси и условию доказываемого утверждения произвольная точка P прямой l имеет равные степени относительно окружностей a и b и равные степени относительно
126

окружностей b и g и, значит, равные степени относительно окружностей a и g. Поэтому точка P принадлежит радикальной оси окружностей a и g. Поскольку P — любая точка прямой l, то l — радикальная ось окружностей a и g. Каждая из трех прямых, содержащих центры двух окружностей, перпендикулярна l. Следовательно, эти три прямые совпадают, т. е. центры окружностей a, b, g коллинеарны.
Важным примером множества окружностей, каждые две из которых имеют одну и ту же радикальную ось, является множество всех окружностей, имеющих две общие точки A и B. Тогда прямая AB и есть радикальная ось каждых двух окружностей из этого множества (рис. 125). Как увидим далее, этот пример не является единственным.
О п р е д е л е н и е. Множество всех окружностей, каждые две из которых имеют одну и ту же радикальную ось l, называется пучком окружностей. Прямая l называется радикальной осью этого пучка.
Центры всех окружностей пучка лежат на одной прямой, перпендикулярной его радикальной оси.
Рассмотрим три возможных случая, приводящих к классификации пучков окружностей.
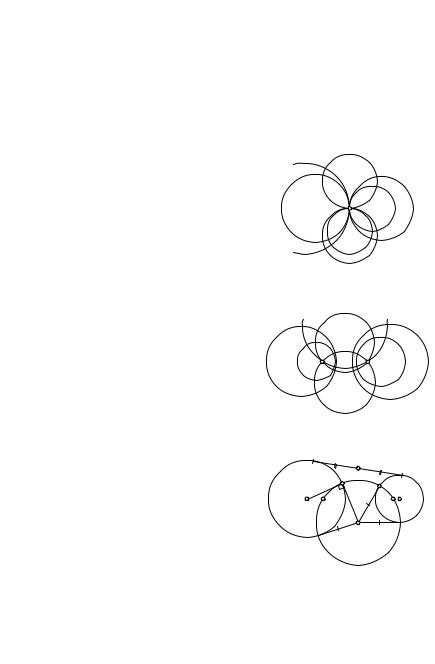
1)Пусть какие-либо две окружности пучка пересекаются в точках A
иB. Тогда эти точки принадлежат их радикальной оси и должны иметь равные (нулевые) степени относительно каждой окружности пучка. Следовательно, любая окружность пучка проходит через эти точки. Таким образом, пучок состоит из окружностей, имеющих две общие точки. Такой пучок называется пучком пересекающихся окружностей,
или эллиптическим пучком окружностей (рис. 125).
2) Пусть какие-либо две окружности пуч-
A
ка касаются в точке A (внутренним или внешним образом). Тогда их радикальная ось l
lесть общая касательная к ним в точке A. Любая третья окружность пучка по определе-
Рис. 126 |
нию имеет ту же радикальную ось с первыми |
|
двумя и потому касается прямой l в точке A. |
Итак, пучок состоит из всех окружностей, попарно касающихся в общей точке. Такой пучок называется параболическим пучком окружностей (рис. 126).
3) Пусть какие-либо две окружности пучка не имеют общих точек. Тогда и любые две окружности этого пучка не будут иметь общих точек,
127
так как в противном случае через их общие точки проходили бы все |
|||
окружности пучка. Но выбранные первоначально две окружности пуч- |
|||
ка не пересекаются. Пучок непересекающихся окружностей называется |
|||
гиперболическим пучком окружностей. Построение окружностей этого |
|||
пучка рассмотрим чуть позже. |
|||
17.2. Критерии пучка окружностей. Задание пучка. Докажем два |
|||
необходимых и достаточных условия того, что некоторое множество |
|||
окружностей есть пучок. |
|
||
К р и т е р и й 1. Множество всех окружностей, ортогональных од- |
|||
ной окружности, центры которых лежат на одной прямой, есть пу- |
|||
чок окружностей. |
|
|
|
В самом деле, возьмем две произвольные окружности a1 и a2 из |
|||
заданного множества M окружностей, центры которых лежат на пря- |
|||
мой m и которые ортогональны данной окружности w с центром A |
|||
(рис. 127). По свойству 1◦ точек радикальной оси (п. 16.3) точка A при- |
|||
надлежит радикальной оси l окружностей a1 и a2. Но эта прямая l не |
|||
зависит от выбора окружностей a1 и a2 из заданного множества M, так |
|||
как она проходит через постоянную точку A перпендикулярно задан- |
|||
ной прямой m. Итак, любые две окружности заданного множества M |
|||
имеют одну и ту же радикальную ось. Следовательно, это множество M |
|||
|
|
|
окружностей принадлежит пучку окружно- |
|
|
|
стей с радикальной осью l. |
|
|
|
Обратно, пусть x — произвольная окруж- |
|
A |
w |
ность пучка с радикальной осью l, которо- |
|
|
му принадлежат окружности a1 и a2. Тогда |
|
|
|
|
ее центр лежит на линии центров окружно- |
|
|
m¯ |
стей a1 и a2, т. е. на прямой m, и окруж- |
|
|
ность x ортогональна w (свойство 1◦ точек |
|
O1 |
O2 |
|
|
|
радикальной оси). Итак, заданное множе- |
||
|
|
a2 |
|
a1 |
l |
|
ство M окружностей есть пучок окружно- |
Рис. 127 |
|
стей. |
|
|
Следствие. Если некоторая окружность |
||
|
|
|
ортогональна двум окружностям пучка, то |
|
|
|
она ортогональна каждой окружности это- |
го пучка.
К р и т е р и й 2. Множество всех окружностей, ортогональных двум данным окружностям, есть пучок окружностей.
Действительно, центры всех окружностей заданного множества принадлежат радикальной оси двух данных окружностей. На основании критерия 1 это множество окружностей есть пучок окружностей.
128
Из определения пучка окружностей и его критериев вытекают способы задания пучка окружностей:
1)двумя принадлежащими ему окружностями,
2)окружностью этого пучка и его радикальной осью,
3)линией центров окружностей пучка и одной ортогональной им окружностью,
4)двумя окружностями, ортогональными окружностям пучка.
17.3. Ортогональные пучки окружностей. Из следствия и кри-
терия 2 предыдущего пункта следует, что существует бесконечное
множество окружностей, каждая из ко- |
|
|
|
|
|
|
|
|
|
|
торых ортогональна каждой окружно- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сти данного пучка окружностей, и это |
|
|
|
|
|
|
|
|
|
|
множество есть также пучок окружно- |
|
|
|
|
|
|
|
|
|
|
стей. Такие два пучка окружностей на- |
|
|
|
|
|
|
|
|
|
|
зываются ортогональными или сопря- |
|
|
|
|
|
|
|
|
|
|
женными пучками окружностей. Ради- |
|
|
|
|
|
|
|
|
|
|
кальная ось одного из них является ли- |
|
|
|
|
|
|
|
|
|
|
нией центров другого и наоборот. |
|
|
|
|
|
|
|
|
|
|
Ясно, что если один из двух ор- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тогональных пучков окружностей па- |
|
|
Рис. 128 |
|
|
|||||
раболический, то и второй также па- |
|
|
|
|
|
|
|
|
|
|
раболический (рис. 128). Если же дан- |
|
|
|
|
|
|
|
|
|
|
ный пучок гиперболический, то ортого- |
|
|
|
|
|
|
|
|
|
|
нальный ему пучок является эллипти- |
|
|
|
|
|
|
|
|
|
|
ческим, и наоборот (рис. 129). Однако |
|
|
I1 |
|
|
|
I2 |
|
|
|
этот факт требует пояснения. Пусть да- |
|
|
|
|
|
|
|
|
|
|
ны две непересекающиеся окружности a |
|
|
|
|
|
|
|
|
|
|
и b. Построим их радикальную ось l и |
|
|
Рис. 129 |
|
|
|||||
возьмем на ней произвольную точку A |
|
|
|
|
||||||
(рис. 130). Длина r касательных из точ- |
|
|
|
|
|
l |
|
|
||
|
|
|
|
|
|
|
||||
ки A к окружностям a и b больше, чем |
a |
|
|
|
|
|
||||
|
T |
|
|
|
|
b |
||||
расстояние от точки A до линии O1O2 |
|
|
|
|
|
|||||
|
|
O1 |
|
|
|
|
|
O2 |
||
центров окружностей. Поэтому окруж- |
|
|
|
|
|
|
|
|||
|
|
I1 |
|
|
|
|
|
I2 |
||
ность w(A, r) пересекает прямую O1O2 в |
|
|
r |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
двух точках I1, I2. Итак, произвольная |
|
|
|
|
|
A |
|
|
||
окружность w пучка окружностей, ор- |
|
|
|
|
|
|
|
|
w |
|
|
|
|
|
|
|
|
|
|||
тогонального данному гиперболическо- |
|
|
|
|
|
|
|
|
|
|
му пучку, пересекает радикальную ось |
|
|
Рис. 130 |
|
|
|||||
O1O2 своего пучка. Через точки пе- |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
ресечения проходят все окружности пучка, |
т. е. он |
эллиптический. |
||||||||
129
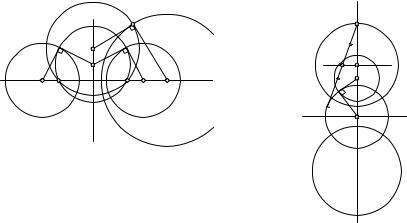
Общие точки I1 и I2 окружностей эллиптического пучка называются предельными точками ортогонального ему гиперболического пучка.
17.4. Задание окружности данного пучка. Если задан пучок окружностей, то некоторую его окружность можно выделить из пучка заданием одной ее точки, так как имеет место теорема.
Теорема. Через каждую точку плоскости, не принадлежащую радикальной оси пучка окружностей, проходит одна и только одна окружность этого пучка.
Д о к а з а т е л ь с т в о. Для эллиптического и параболического пучков теорема очевидна (рис. 125 и 126). В первом пучке эта окружность определяется тремя неколлинеарными точками, а во втором — двумя точками и касательной в одной из них. Рассмотрим гиперболический пучок окружностей.
Пусть он задан непересекающимися окружностями a1 и a2 (рис.131) и дана точка M, не принадлежащая радикальной оси l этих окружностей. Построим произвольную окружность w, ортогональную окружностям a1 и a2. Она принадлежит сопряженному пучку окружностей, который является эллиптическим. Поэтому легко строится окружность b этого пучка, содержащая заданную точку M (она описана около треугольника I1I2M). Теперь осталось построить искомую окружность x, которая проходит через M и ортогональна b. Касательная к b в точке M пересекает прямую O1O2 в центре X этой окружности.
b |
w |
M |
M |
|
|
||||
x |
x |
|||
|
|
B |
a2 |
|
m |
A |
X |
O1 I1 |
I2 O2 X |
|
|
|
a1 |
a2 |
l |
O |
g |
|
||||
|
l |
|
|
a1 |
|
Рис. 131 |
|
|
|
Остался без внимания один частный случай, |
|
|
|
|
когда M (O1O2). Тогда предыдущий способ бес- |
|
|
|
|
силен, хотя искомая окружность x существует. |
|
|
|
|
В этом случае построим окружность g с центром |
|
Рис. 132 |
|
|
в точке O пересечения радикальной оси l и линии |
|
|
|
|
130
