Элементарная математика / Ponarin-I

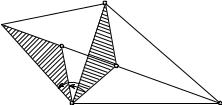
ший, так как длина MN моста определена шириной реки, а сумма AM + NB = A1N + NB минимальна.

З а д а ч а 3. В данном остроугольном треугольнике ABC найти точку P , для которой сумма расстояний до вершин треугольника минимальна (задача Ф е р м а).

Р е ш е н и е. Используем поворот около вершины B на 60◦. Пусть при этом повороте A→A1, P →P1 (рис.102). Так как треугольник BP P1 равносторонний, то BP = P P1 и поэтому P A+ P B + P C = P1A1 + P1P + P C. Эта сумма минимальна тогда и только тогда, когда точки A1, P1, P , C коллинеарны. В этом случае BP C = 120◦ и AP B = A1P1B = 120◦. Поэтому и AP C = 120◦. Итак, искомой точкой P является точка, из которой каждая сторона треугольника ABC видна под углом 120◦. Она называется точкой Торричелли треугольника. Четырехугольник AP BA1 является вписанным в окружность. Поэтому точку Торричелли треугольника ABC можно построить как точку пересечения прямой CA1 и окружности, описанной около правильного треугольника ABA1.

A

A1

P1

P

B C

Рис. 102

В этой задаче вершины треугольника ABC равноправны. Поэтому точку Торричелли можно построить еще и как точку пересечения прямых, соединяющих вершины данного треугольника с третьими вершинами правильных треугольников, построенных на его сторонах во внешнюю сторону (рис. 64).

Требование остроугольности треугольника ABC завышено: решение остается в силе, когда углы треугольника не больше 120◦. ЕслиA = 120◦, то точка P совпадает с вершиной A.

14.5. Экстремальные значения квадратного трехчлена. Если исследуемая функция является квадратичной y = ax2 + bx + c, то она всегда имеет единственное экстремальное значение — минимальное при a > 0, максимальное при a < 0, которое достигается при x = −b/2. Если b2 −4ac >0, то это значение x совпадает с серединой промежутка между корнями трехчлена.

111

Эти свойства можно использовать в геометрических задачах.

З а д а ч а 1. На сторонах AB, BC, CD, DA квадрата ABCD взяты соответственно точки A1, B1, C1, D1 так, что AA1 = BB1 = CC1 = DD1 (рис. 103). При каком отношении AA1 : AB площадь четырехугольника A1B1C1D1 наименьшая?

Р е ш е н и е. Пусть AB = 1, AA1 = x. Четырехугольник A1B1C1D1 является квадратом (поворот около центра данного квадрата на 90◦). Его площадь равна A1B12 = x2 + (1 − x)2 = 2x2 − 2x + 1.

наибольшее значение при x = R. А тогда и y = R. Итак, наибольший периметр имеет трапеция, у которой боковые стороны и меньшее основание равны радиусу окружности.

З а д а ч а 3. На сторонах AB и BC прямоугольника ABCD даны точки N и P , BN = n, BP = m. Через произвольную точку M отрезка P N проведены прямые ME и MF , параллельные сторонам прямоугольника (рис. 104). Найти максимальное и минимальное значение площади S прямоугольника MF DE, если BC = a, AB = b.

112

Р е ш е н и е. Пусть x, y — длины сторон DE и EM прямоугольника MF DE. Тогда MK = EA = a − x, KN = AK − AN = y + n − b. Из

y = m1 (−nx + an + bm − mn). Поэтому

S = xy = m1 (−nx2 + (an + bm − mn)x), x > a − m.

Так как a > m и b > n, то an + bm − mn = (a − m)n + bm > 0. Функция

−nx2 + (an + bm − mn)x имеет максимум при x0 = an + bm − mn.

2n

Исследуем, при каком условии x0 6 a. Неравенство

an + bm − mn

2n

6 a

эквивалентно условию mn > bm − an, или nb − ma 6 1. При этом условии площадь S прямоугольника MF DE максимальна и равна

(an + bm − mn)2

4mn

.

При nb − ma > 1 будет x0 > a. В этом случае на промежутке [a − m, a] функция S строго возрастает. Поэтому она принимает при x = a − m минимальное значение b(a − m) и при x = a максимальное значение a(b − n). Итак, площадь S прямоугольника MF DE минимальна, когда точка M совпадает с P . Свое максимальное значение она принимает при mn > bm −an во внутренней точке M отрезка P N, а при mn < bm −an —

вконечной точке N.

Вслучае максимума площади S для внутренней точки M отрезка P N эту точку M можно построить с помощью отрезка DE = x0 по полученной формуле, представив ее в виде:

1 bm x0 = 2 (a − m) + n .

Искомый отрезок DE равен полусумме отрезков CP = a −m и BT = bmn

при условии AT k P N:

DE = 12 (CP + BT ), AT k P N.

Это значит, что отрезок DE равен средней линии любой трапеции с основаниями, равными CP и BT . Условие DE > CP (x > a − m) эквивалентно BT > CP . В случае, когда BT = CP , т. е. когда mn = an − bm максимальное значение достигается при M = P .

113

Упражнения

14.1.Из всех прямоугольных треугольников с данной высотой найдите треугольник наименьшего периметра.

14.2.Дан острый угол и на одной его стороне отрезок AB. Постройте на другой стороне угла такую точку C, чтобы угол ACB был наибольшим.

14.3.Внутри квадрата дана точка M. Проведите через нее прямую, отсекающую от квадрата треугольник а) минимальной площади, б) максимальной площади.

14.4.Из всех прямоугольных треугольников найдите тот, у которого

14.8.Найдите внутри данного треугольника точку, произведение расстояний от которой до сторон треугольника максимально.

14.9.Внутри треугольника ABC взята точка M, через которую проведены прямые MA, MB, MC, пересекающие соответственно стороны

троиде треугольника.

14.10.Через точку M, лежащую внутри остроугольного треугольника ABC, проведены прямые MA, MB, MC, пересекающие стороны BC, CA, AB соответственно в точках A1, B1, C1. При каком положении точки M периметр треугольника A1B1C1 наименьший?

14.11.Проведите через вершину A треугольника ABC прямую так, чтобы сумма расстояний до нее от вершин B и C была наибольшей. Рассмотрите случаи острого, прямого и тупого углов с данной вершиной треугольника.

14.12.На основании AB трапеции ABCD дана точка M. Постройте на основании CD такую точку N, чтобы площадь четырехугольника, полученного при пересечении прямых AN, BN, CM, DM, была наибольшей.

114

14.13. Докажите, что минимальная сумма расстояний внутренней точки треугольника до его вершин равна

r12 (a2 + b2 + c2 + 4√3S).

§15. Экстремальные свойства правильных многоугольников

метра наибольшую площадь имеет правильный треугольник. В § 12 было доказано, что из всех четырехугольников с данными сторонами наибольшую площадь имеет вписанный четырехугольник. Его всегда можно построить (упр. 7.24). Покажем, что из всех прямоугольников данного периметра 2p наибольшую площадь имеет квадрат. Действительно, площадь S прямоугольника равна

S = x(p − x) = p2 − p − x 2,

4 2

откуда видно, что максимальна она тогда и только тогда, когда p/2 −x= = 0, т.е. когда x = p −x = p/2. Следовательно, прямоугольник — квадрат.

Такого рода задачи называют изопериметрическими задачами. В общей формулировке изопериметрическая задача такова: среди плоских фигур заданного множества, имеющих равные периметры (длины граничных кривых), найти ту, которая имеет наибольшую площадь.

Эта сложная задача решалась для различных множеств фигур в течение XVIII—XIX веков швейцарскими геометрами Г.Крамером, С.Люилье и Я.Штейнером. Основным методом решения изопериметрических задач служит вариационное исчисление.

Я. Штейнер доказал, что из всех плоских фигур данного периметра наибольшую площадь имеет круг. Доказательство Штейнера кратко и изящно, но содержит существенный пробел: он предположил (но не доказал), что фигура максимальной площади существует. А это представляет собой одну из трудных задач, решение которой далеко не элементарно.

Ниже рассмотрим решение (неполное) изопериметрической задачи для многоугольников. Предположив существование многоугольника заданного периметра и имеющего максимальную площадь, докажем, что таковым является правильный многоугольник и только он.

15.2. Общие свойства изопериметрических фигур максимальной площади рассмотрим для множества многоугольников.

115

1◦. Многоугольник, имеющий заданный периметр и наибольшую площадь, необходимо выпуклый. В самом деле, если бы невыпуклый многоугольник ABCDE (рис. 106) данного периметра имел наибольшую площадь, то, отразив вершину A его угла, большего 180◦, от внешней диагонали BE в точку F , мы получили бы многоугольник BCDEF большей площади и того же периметра.

2◦. Всякая прямая, делящая пополам заданный периметр многоугольника максимальной площади, делит пополам и его площадь.

Это свойство также просто доказывается с помощью осевой симметрии методом от противного. Пусть прямая m делит пополам периметр многоугольника ABCDE (рис. 107), т. е. P A + AB + BQ = P E + ED + + DC + CQ, но не делит пополам его площадь: SPEDCQ > SPABQ. Отразив многоугольник P EDCQ от этой прямой m, получим многоугольник P EDCQC0D0E0, имеющий вдвое большую площадь, чем SPEDCQ, т. е. большую, чем площадь данного многоугольника ABCDE, и равный с ним периметр. Если полученный многоугольник невыпуклый, то согласно 1◦ его можно заменить многоугольником того же периметра еще большей площади.

E

C

Для множества произвольных плоских фигур доказательства этих двух свойств по существу ничем не отличаются от изложенных. Они принадлежат Я. Штейнеру.

15.3. Две подготовительные задачи, которые будут нужны для доказательства основного экстремального свойства правильных многоугольников.

З а д а ч а 1. Из всех треугольников, имеющих данную сторону c и данный периметр 2p, найти треугольник наибольшей площади.

Р е ш е н и е. По формуле Герона S2 = p(p − a)(p − b)(p − c), где p и p − c постоянны. Поэтому S максимальна тогда и только тогда, когда

116

при вершинах Ai и Ai+1. Для другой касательной A0iA0i+1 площадь многоугольника A1A2 . . . A0iA0i+1 . . . An будет меньше, а периметр останется

тем же, так как A0iAi + AiAi+1 = Ai+1A0i+1 + A0i+1A0i (это следует из описанных четырехугольников AiBCAi+1, и A0iBCA0i+1).

В третьем случае, когда Ai−1Ai kAi+1Ai+2 (рис.111), проведем диагональ Ai−1Ai+2. Полученная трапеция имеет заданную высоту h, заданный периметр и заданную боковую сторону Ai−1Ai+2. Следовательно, будет постоянна сумма l = a + b + x, x =

в котором равенство достигается лишь для правильного n-угольника. Из неравенства (15.1) следует, что из всех n-угольников данной площади S (при фиксированном n) наименьший периметр имеет правиль-

ный n-угольник.

15.5. Экстремальное свойство правильного многоугольника из множества многоугольников, вписанных в данную окружность. Из множества всех n-угольников с данным числом сторон, вписанных в одну окружность, правильный многоугольник имеет наибольшую площадь

инаибольший периметр.

До к а з а т е л ь с т в о. Пусть вписанный в данную окружность w n- угольник M не является правильным. Тогда у него обязательно найдется сторона, меньшая стороны a вписанного в эту окружность правильного n-угольника M0. He сужая общности доказательства, можно полагать также, что у M имеется сторона, большая a. Этого не слу-

119

SM0 > SMi > SM .

Доказательство максимальности периметра по существу не отличается от предыдущего с той лишь разницей, что приходится использовать свойство, доказанное в п. 14.2 (задача 1), согласно которому из двух вписанных треугольников, имеющих общую сторону, больший периметр имеет тот, у которого больше высота, опущенная на эту сторону.

15.6. Экстремальное свойство правильного многоугольника из множества многоугольников, описанных около одной окружности. Из множества всех n-угольников с данным числом сторон, описанных около одной окружности, правильный n-угольник имеет наименьшую площадь и наименьший периметр.

120