Элементарная математика / Ponarin-I

2.75.Через точку пересечения хорд AC и BD окружности проведены прямые m и n, перпендикулярные к прямым AB и CD соответственно. Докажите, что (m, (AC)) = (n, (BD)).

2.76.При подобии f второго рода f(a) = b и f(b) = c. Докажите, что прямые a и c параллельны.

2.77.В треугольнике ABC AC > CB. Касательная в точке C к описанной около треугольника окружности пересекает прямую AB в точке D. Точки M и N — середины отрезков BD и CD соответственно. Докажите, что биссектриса угла ADC образует равные углы с прямыми AN и CM.

2.78.В трапеции ABCD с основаниями AB и CD диагонали пересекаются в точке O. Точки A1 и B1 симметричны точкам A и B относительно биссектрисы угла AOB. Докажите, что углы ACA1 и BDB1 равны.

2.79.Даны точки A(2; 1) и B(−3; 2), имеющие указанные координаты относительно некоторой прямоугольной декартовой системы координат. Постройте ее оси и базисные векторы.

2.80.Постройте правильный треугольник, две вершины которого принадлежат данной окружности, а проекция одной из них на противоположную сторону совпадает с данной точкой.

2.81.Постройте четырехугольник по четырем его сторонам, если около него можно описать окружность.

2.82.Постройте треугольник, подобный данному треугольнику, так, чтобы его вершины лежали по одной на трех данных параллельных прямых.

2.83.Точки M1, M2, M3 являются образами точки M при поворотах

коллинеарны, если a = b = 180◦, g = −90◦.

2.85.Постройте треугольник, подобный данному треугольнику, так, чтобы одна его вершина находилась в данной точке, а две другие лежали по одной на двух данных окружностях.

2.86.Постройте параллелограмм по отношению диагоналей и углу между ними так, чтобы его вершины лежали по одной на прямых, содержащих стороны данного параллелограмма ABCD.

2.87.Даны две окружности, прямая l и принадлежащая ей точка A. Постройте треугольник ABC такой, что прямая l содержит биссектрису угла A, вершины B и C лежат соответственно на данных окружностях

иотношение сторон AB и AC равно отношению двух данных отрезков.

241

2.88.Подобие первого рода задано парой соответственных точек, коэффициентом и углом. Постройте центр этого подобия.

2.89.Подобие второго рода задано своей осью и парой соответственных точек. Постройте центр подобия и найдите его коэффициент.

2.90.На окружности даны четыре точки. Среди расстояний между ними нет равных. Найдите множество центров подобий второго рода, при которых любые две из данных точек отображаются на две оставшиеся.

2.91.Неравные отрезки AB и A1B1 лежат на одной прямой. Постройте двойные прямые подобия второго рода, заданного парами точек

A→ A1, B → B1.

2.92.Докажите, что центры подобий первого и второго рода, при

которых один из данных неравных квадратов отображается на другой (8 центров), принадлежат одной окружности.

2.93. В треугольнике ABC проведены высоты AA1 и BB1. Постройте центр и двойные прямые подобия второго рода, при котором A → A1,

B→ B1.

2.94.Постройте центр подобия, представляющего собой композицию

данной гомотетии и данного гомотетического поворота.

2.95.Даны два подобных противоположно ориентированных треугольника ABC и A1B1C1. Докажите, что отрезки AA1, BB1, CC1 можно разделить в таких равных отношениях, чтобы точки деления принадлежали одной прямой.

2.96.Квадраты ABCD и RP BQ одинаково ориентированы и расположены так, что точки P и Q принадлежат прямым AB и BC соответственно. Докажите, что окружности, построенные на отрезках AR, BP , CB, DQ как на диаметрах, пересекаются в одной точке.

2.97.Даны два правильных противоположно ориентированных треугольника ABC и A1B1C1. Докажите, что тройки точек, делящих отрезки AA1, BB1 и CC1; AB1, BC1 и CA1; AC1, BA1 и CB1 в отношении k = AB : A1B1, принадлежат соответственно трем прямым, которые пересекаются в одной точке.

2.98.На сторонах треугольника ABC построены подобные одинаково ориентированные треугольники ABC1, CBA1, ACB1. Докажите, что C1A1CB1 — параллелограмм.

2.99.Даны два подобных (негомотетичных) одинаково ориентированных треугольника ABC и A1B1C1. Прямые AA1, BB1 и CC1 пересекаются в точке P . Докажите, что точки A, B, C, P принадлежат одной окружности и точки A1, B1, C1, P также принадлежат одной окружности.

2.100*. Треугольники ABC, A1B1C1, A2B2C2 подобны и одинаково ориентированы. Тройки точек A, A1, A2; B, B1, B2; C, C1, C2 коллинеар-

242

ны. Докажите, что центры подобий, отображающих каждый из этих треугольников на другие, совпадают.

2.101.В условиях предыдущей задачи докажите, что точки A, B, C делят соответственно отрезки A1A2, B1B2, C1C2 в равных отношениях.

2.102. На сторонах AB, BC и CA отрицательно ориентированного треугольника ABC с неравными сторонами построены положительно ориентированные подобные треугольники ABP , BCQ, CAR, в которых P = Q = R = 120◦. Докажите, что композиция трех гомотетических поворотов с центрами P , Q, R и некоторым коэффициентом k на углы 120◦ есть гомотетия с центром в точке B.

2.103. Стороны правильного треугольника ABC разделены по обходу его границы в отношении k точками A1, B1, C1. Стороны треугольника A1B1C1 разделены по обходу его границы в отношении 1/k точками A2, B2, C2. Докажите, что треугольники ABC и A2B2C2 гомотетичны. Найдите коэффициент гомотетии. Обобщите результат для правильных многоугольников.

2.104. Докажите, что ортогональные проекции точки описанной около треугольника окружности на прямые, содержащие стороны этого треугольника, лежат на одной прямой (теорема Симсона).

2.105. Боковые стороны AD и BC трапеции ABCD повернуты около своих середин на углы 90◦, после чего они занимают положения A1D1 и B1C1. Докажите, что A1B1 = C1D1.

2.106. Дано множество всех подобных друг другу треугольников ABC, у которых вершина A фиксирована, а вершина B принадлежит данной прямой. Найдите множество вершин C этих треугольников.

2.107. Найдите множество точек пересечения прямых пучка с центром S со своими образами при заданном подобии первого рода.

2.108. Найдите множество точек пересечения прямых пучка параллельных прямых со своими образами при заданном подобии первого и второго рода.

2.109. Окружность a проходит через вершины A и B треугольника ABC. Найдите множество вершин X треугольников AMX, подобных треугольнику ABC и противоположно ориентированных с ним, если вершина M перемещается по окружности a.

2.110. Даны правильные одинаково ориентированные треугольники ABC и A1B1C1. Прямые AB и A1B1, BC и B1C1, CA и C1A1 пересекаются в точках M, N, P соответственно. Докажите, что окружности (MAA1), (NBB1), (P CC1) имеют общую точку.

2.111. Даны два подобных одинаково ориентированных треугольника A1B1C1 и A2B2C2. Отрезки A1A2, B1B2, C1C2 разделены точками A,

243

B, C в одном отношении. Докажите, что треугольник ABC подобен треугольникам A1B1C1 и A2B2C2.

2.112. Даны окружность w и точка M. Найдите множество образов Q

A2 = (BC) ∩ (B1C1), B2 = (CA) ∩ (C1A1), C2 = (AB) ∩ (A1B1) не зависят от угла поворота.

§22. Параллельное проектирование плоскости на плоскость

Зададим две плоскости a и a1 и не параллельную им прямую l. Каждой точке M плоскости a поставим в соответствие такую точку M1 плоскости a1, что прямая MM1 параллельна l. Этим условием задано взаимно однозначное отображение плоскости a на плоскость a1, которое называется параллельным проектированием плоскости a на плоскость a1 в направлении прямой l. Прямые и плоскости, параллельные прямой l, называются проектирующими прямыми и проектирующими плоскостями. Рассмотрим свойства этого отображения.

екций двух отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению данных отрезков.

244

Рассмотрим сначала случай, когда данные отрезки AB и CD лежат на одной прямой (рис. 112). Проектирующие прямые AA1, BB1, CC1, DD1 параллельны и лежат в одной проектирующей плоскости. По те-

ореме о пропорциональных отрезках имеем: AB = A1B1 . Пусть теперь

CD C1D1

С в о й с т в о 4. Параллельное проектирование плоскости на плоскость сохраняет отношение площадей фигур.

Д о к а з а т е л ь с т в о. Пусть фигура F плоскости a имеет площадь S(F ), а ее параллельная проекция F1 на плоскость a1 имеет площадь S(F1). Проведем произвольную плоскость b, перпендикулярную направлению l проектирования. Ортогональные проекции (в направлении l) фигур F и F1 на плоскость b совпадают. Если S0 — площадь этой проекции, то по свойству площади ортогональной проекции фигуры

S0 = S(F ) cos (a, b) = S(F1) cos (a1, b),

откуда

cos (a, b)

S(F1) = S(F ) cos (a1, b) .

Отношение косинусов не зависит от выбора фигуры F в плоскости a. Для любой фигуры Φ и ее параллельной проекции Φ1 на плоскость a1

cos (a, b)

S(Φ1) = S(Φ) cos (a1, b) .

Следовательно, S(F1) = S(F ) .

S(˘1) S(˘)

245

§23. Аффинные отображения

23.1.Определение и задание аффинного преобразования плоскости.

Параллельное проектирование плоскости на плоскость, а также любая композиция таких проектирований называется аффинным отображением плоскости на плоскость. В частности, если данная плоскость совпадает со своим образом при аффинном отображении, то оно является аффинным преобразованием этой плоскости.

Аффинные отображения плоскости на плоскость обладают свойствами 1—4, доказанными в предыдущем параграфе. Иначе говоря,

аффинные отображения отображают каждую прямую на прямую, сохраняют параллельность прямых, отношение коллинеарных отрезков, отношение площадей фигур.

Теорема (о задании аффинного преобразования плоскости). Если A,

B, C — три заданные неколлинеарные точки плоскости и A1, B1, C1 — также наперед заданные неколлинеарные точки этой плоскости, то существует единственное аффинное преобразование плоскости, которое отображает A на A1, B на B1 и C на C1.

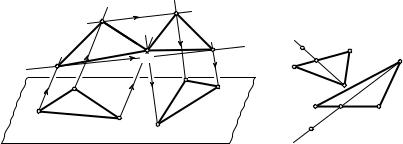
Любой треугольник ABC можно отобразить на любой треугольник A1B1C1, лежащий в плоскости первого треугольника, композицией не более трех параллельных проектирований плоскости на плоскость (рис. 113). Докажите это сами. Эта композиция и есть требуемое аффинное преобразование данной плоскости. Единственность этого аффинного преобразования вытекает из того, что в силу инвариантности коллинеарности точек и отношения коллинеарных отрезков образ M1 произвольной точки M строится однозначно при заданных

Пусть (MC) ∩ (AB) = P . Образом точки P будет точка P1 прямой A1B1

246

C (постоянно для данного сжатия) и называется

коэффициентом сжатия. При k = −1 сжатие называется косой симметрией (рис. 117).

247

Родство можно задать осью l и парой соответственных точек A →A1 (рис. 118). Тогда на основании свойств 1◦ и 3◦ легко строится образ X1 произвольной точки X: (AX) ∩ l = K, (XX1) k

Ak (AA1), (KA1) ∩ (XX1) = X1.

X23.3. Понятие об аффинной геометрии. Ос-

чек A, B, C прямой, 4) отношение площадей фигур. Из этих инвариантов самым главным является первый: теорию аффинных преобразований можно построить на основе одного его, принимая по определению за аффинные преобразования такие преобразования, которые отображают прямые на прямые. Теорию инвариантов аффинных преобразований называют аффинной геометрией.

Поскольку аффинные преобразования не сохраняют длину отрезка и величину угла, то в аффинной геометрии нет этих понятий — нет метрики — и поэтому нет понятий, базирующихся на них. Например, в аффинной геометрии отсутствуют перпендикулярные прямые, окружности, правильные треугольники, прямоугольники и др.

Свойство фигуры называется аффинным (относится к аффинной геометрии), если оно не изменяется при всех аффинных преобразованиях. Фигура называется аффинной, если ее характеристическое (определяющее) свойство является аффинным. Вот примеры. Параллелограмм — фигура аффинная, поскольку его характеристическим свойством служит аффинный инвариант — параллельность прямых. Луч, угол, трапеция, многоугольник — также аффинные фигуры. К аффинной геометрии относятся понятия медианы и средней линии треугольника, так как середина C отрезка AB может быть определена как точка, для которой AC/CB = 1. Поэтому теоремы о средней линии треугольника, о средней линии трапеции, о пересечении медиан треугольника, о точке пересечения диагоналей параллелограмма — аффинные теоремы. К аффинной геометрии относятся теорема Паппа и теорема Менелая, доказанные в § 15.

С движениями связано понятие равных (конгруэнтных) фигур; с подобиями — понятие подобных фигур. Аналогично им в аффинной геометрии определяется понятие аффинно эквивалентных фигур. Две фигуры называются аффинно эквивалентными, если существует аффинное преобразование, отображающее одну из них на другую.

248

Обратимся к примерам. Согласно теореме о задании аффинного преобразования плоскости любые два треугольника аффинно эквивалентны: существует шесть аффинных преобразований, каждое из которых отображает один из них на другой. Поэтому в аффинной геометрии треугольники нельзя классифицировать или хотя бы выделить какие-либо их виды. Правильный треугольник аффинно эквивалентен любому треугольнику. Отсюда следует, что будут аффинно эквивалентны любые два параллелограмма ABCD и MNP Q. В самом деле, зададим аффинное преобразование плоскости парами точек A →M, B →N, C →P . Тогда в силу инвариантности параллельности прямых при аффинных преобразованиях (CD) → (P Q), (AD) → (MQ) и, значит, D → Q.

Следовательно, в аффинной геометрии из множества параллелограммов нельзя выделить ромбы, прямоугольники, квадраты.

Для произвольных трапеций ABCD и MNP Q (с основаниями AB

иMN) дело обстоит иначе. Указанное аффинное преобразование переводит D в Q лишь тогда, когда AB : CD = MN : P Q. Это — необходимое

идостаточное условие аффинной эквивалентности двух трапеций.

Докажите, что два четырехугольника аффинно эквивалентны лишь тогда, когда точки пересечения их диагоналей делят диагонали в соответственно равных отношениях.

Так как все аффинные инварианты являются также инвариантами движений и подобий, то аффинная геометрия полностью входит в евклидову геометрию. Однако аффинную геометрию можно рассматривать и построить независимо от евклидовой геометрии.

§24. Решение задач с помощью аффинных преобразований

Метод аффинных преобразований применим лишь к решению аффинных задач, т. е. таких задач, в которых используются аффинные и только аффинные свойства фигур. С помощью аффинных преобразований эти задачи могут решаться или непосредственно, или же путем сведения к другим методам. Сущность второго способа состоит в следующем. Некоторым аффинным преобразованием рассматриваемая фигура Φ отображается на такую фигуру Φ0, которая с метрической (евклидовой) точки зрения является более простой, чем данная. Все аффинные свойства полученной фигуры Φ0 совпадают с аффинными свойствами ее прообраза Φ. Хотя метрические свойства этих фигур неодинаковы, но это различие не может сказаться на окончательном результате в силу аффинности задачи. Данная задача решается для

249

фигуры Φ0 любыми средствами. Полученный результат, являясь аффинным инвариантом, имеет силу и для фигуры Φ.

Проиллюстрируем сказанное на примерах.

З а д а ч а 1. Доказать, что во всякой трапеции точка пересечения диагоналей, точка пересечения прямых, содержащих боковые стороны,

исередины оснований лежат на одной прямой.

Ре ш е н и е. Задача свободна от метрических понятий и поэтому допускает решение аффинным методом. Рассмотрим равнобочную трапецию, аффинно эквивалентную данной. Прямая, содержащая середины оснований равнобочной трапеции, служит ее осью симметрии и поэтому содержит точку пересечения продолжений боковых сторон.

Можно решить задачу и непосредственно для данной трапеции, применяя косую симметрию относительно прямой, проходящей через середины оснований.

З а д а ч а 2. Точки M и N — середины сторон соответственно BC и CD параллелограмма ABCD. Найти отношения, в которых точка P пересечения отрезков AM и BN делит эти отрезки.

Р е ш е н и е. Задача аффинная. Искомые отношения не зависят от вида параллелограмма. Данный параллелограмм ABCD аффинно эквивалентен любому квадрату A1B1C1D1, при этом середины M1 и N1 сторон B1C1 и C1D1 квадрата являются образами точек M и N при аффинном преобразовании, отображающем параллелограмм ABCD на этот квадрат. Поэтому оно отображает точку P на точку P1 пересечения отрезков A1M1 и B1N1. По свойству аффинного преобразования

упрощается, так как A1M1 B1N1 (примените поворот около центра квадрата на 90◦). Положим A1B1 = 2. Тогда из прямоугольного тре-

угольника A1B1M1 имеем: A1P 1 = 22 = 4. Если Q1 — ортогональная про-

P1M1 12

екция точки C1 на (B1N1), то по доказанному B1Q1 : Q1N1 = 4. Поскольку P1 — середина B1Q1, то B1P1 : P1N1 = 2 : 3. Итак, AP : P M = 4

иBP : P N = 23 .

За д а ч а 3. Стороны BC, CA, AB треугольника ABC разделены

соответственно точками A1, B1, C1 в отношении 1 : 3. Найти отношение площади треугольника ABC к площади треугольника с вершинами в точках пересечения прямых AA1, BB1, CC1.

Р е ш е н и е. Аффинный характер задачи не вызывает сомнений. Треугольник ABC аффинно эквивалентен правильному треугольнику. Решим задачу для правильного треугольника, обозначая его снова через ABC (рис. 119). Если (AA1) ∩ (BB1) = C0, (BB1) ∩ (CC1) = A0,

250