4.8. Функциональная полнота систем

Функционально полной называется такая система функций , через функции которой можно выразить любую логическую функцию.

Например, . Эта система функционально полна, так как любая функция имеет булеву формулу.

Теорема.

Произвольная система будет функционально полной, если она сводится к функционально полной системе.

Это означает, что через функции системы можно выразить все функции системы.

Лемма 1.

Если функция – немонотонна, то подстановкойn-1 константы из нее можно получить отрицание.

Лемма 2.

Если функция – нелинейна, то подстановкойn-2 констант из нее можно получить дизъюнкцию и конъюнкцию.

Функционально полной в слабом смысле называется такая система функций , которая становится функционально полной, если к ней добавить константы 0 и 1.

Например, – функционально полна в слабом смысле. Эта система функционально алгебры Жегалкина. Для того, чтоб с ее помощью можно было записать все полиномы Жегалкина, необходимо добавить константу 1. Это означает, что– функционально полна (в сильном смысле).

Теорема 1 о функциональной полноте.

Для того чтобы система функций была функционально полна в слабом смысле, необходимо и достаточно, чтобы она содержала хотя бы одну немонотонную и хотя бы одну нелинейную функцию.

Лемма 3.

Если функция – несамодвойственна, то подстановкой отрицания из нее можно получить константы 0 и 1.

Теорема 2 о функциональной полноте (теорема Поста).

Для того чтобы система функций была функционально полна (в сильном смысле), необходимо и достаточно, чтобы она содержала

хотя бы одну немонотонную,

хотя бы одну нелинейную,

хотя бы одну несамодвойственную,

хотя бы одну не сохраняющую 0,

хотя бы одну не сохраняющую 1 функцию.

Упражнения

1. Проверить монотонность функции, используя определение.

1. ;

2. ;

3. _;

4. _;

5. .

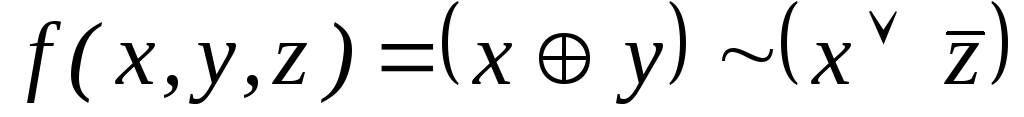1. Проверить монотонность функции, используя теорему о булевой формуле монотонной функции.

1. ;

2. ;

3. ;

4. ;

5. .

3. С помощью немонотонной функции и подстановки констант получить отрицание, используя лемму 1.

1. ; 2) ;

2. ; 4) .

4. С помощью нелинейной функции и отрицания подстановкой констант получить дизъюнкцию или конъюнкцию, используя лемму 1

1. ;

2. ;

3. .

5. Проверить функциональную полноту системы логических функций. Построить таблицу Поста, сделать вывод.

1. ; 3) ; 5);

2) ; 4); 6).

5. Привести выражение к формуле, выраженной через функционально полную систему ,,,:

   1. 

   2. 

   3. 

   4. 

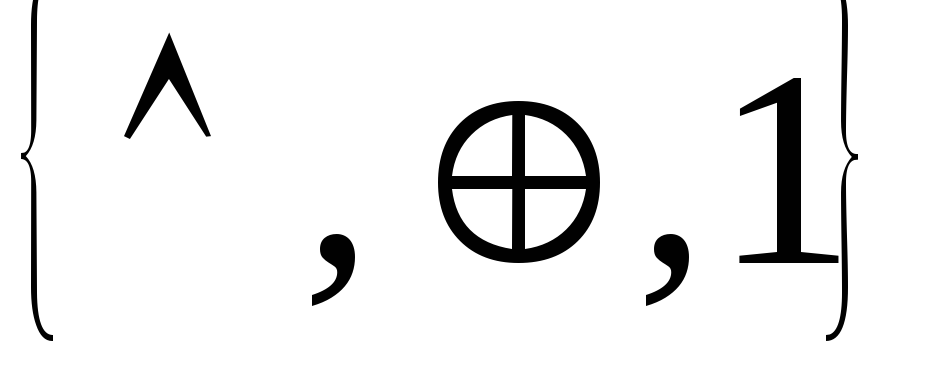6. Система состоит из одной логической функции, заданной своим вектор-столбцом. Построить таблицу Поста и сделать вывод о функциональной полноте данной системы.

1) ; 5)

2) ; 6)

3) ; 7).

4) ;

Глава 5. Логика высказываний и логика предикатов

5.1. Логика высказываний

Высказывание – это утверждение или повествовательное предложение, которое может быть либо истинным, либо ложным.

Значением истинного высказывания является «И» – истина, ложного – «ложь».

Повелительные («Войдите, пожалуйста»), вопросительные («Который час?») и бессмысленные предложения («Сумма пяти и восемнадцати»), в которых ничего не утверждается, не являются высказываниями.

Предметом логики является анализ различных логических связей и методы построения на их основе правильных логических рассуждений.

Способы построения новых высказываний из заданных с помощью логических связок и способы установления истинности высказываний, построенных таким образом, изучаются в логике высказываний.

Основные логические связки  это связки: и, или, не, если … то…, которые в логике высказываний имеют специальные названия и обозначения. Иногда к ним добавляют еще две связки либо …, либо …(или …, или …); если, и только если (тогда и только тогда).

Для одной и той же связки в разных источниках используются разные названия и обозначения, которые приведены в таблице 1.

Таблица 1

Связка	Название	Обозначение	Высказывание, полученное с помощью связки	Математическая запись
1. и	конъюнкция (или логическое умножение)		А и В	А  В А В А В, АВ
2. или	дизъюнкция		А или В	А  В А+ В
3. не	отрицание, инверсия		не А	, А
4. если …, то …	импликация		если А, то В (А влечет В)
5. либо …, либо …	исключающее «или», неравнозначность	, 	либо А, либо В	А  В А В
6. если и только если	эквивалентность, равнозначность	~, 	А, если и только если В	А  В А~ В

В последней колонке табл. 1 записаны формулы, или выражения логики высказываний. С помощью букв А, В, С, ... обозначающих высказывания, связок и скобок можно построить разнообразные формулы.

Исследование свойств таких формул и способов установления их истинности и является основным предметом логики высказываний.

Существуют два подхода к построению логики высказываний, которые образуют два варианта этой логики: алгебру логики и исчисление высказываний.