9. Полугруппы, группы, решетки

Алгебра с одной бинарной ассоциативной операцией называется полугруппой. Эта операция обычно называется умножением и обозначается илиab. Такая запись называется мультипликативной. В частности аа обозначается как ,ааа как и т. д. В общем случае.Полугруппа называется коммутативной, если операция умножения коммутативна. Если полугруппа содержит такой элемент е, что для любого а выполняется , то такой элемент называетсяединицей. Полугруппа с единицей называется моноидом.

Пример 1.

Множество действительных чисел с операцией умножения является полугруппой с единицей. Здесь е = 1.

Утверждение 1.

Единица в полугруппе всегда единственна.

Группой называется полугруппа с единицей, в которой для каждого элемента а существует обратный элемент , удовлетворяющий условию .

Утверждение 2.

Для каждого элемента а в группе существует единственный обратный элемент .

Число элементов группы называется порядком группы. Группа называется абелевой, если операция группы коммутативна. Группа, все элементы которой является степенями одного и того же элемента а, называется циклической.

Утверждение 3.

Циклическая группа всегда абелева.

Пример 2.

Множество целых чисел с операцией сложения является циклической.

Пример 3.

Множество целых чисел с операцией сложения является абелевой группой. Единицей по сложению является . Для каждого числасуществует обратный (здесь:противоположный) – z < 0. И наоборот. Для числа 0 противоположным является число 0.

Множество, на котором кроме операций заданы отношения называется алгебраической системой. Таким образом, алгебра является частным случаем алгебраической системы.

Рассмотрим частный случай алгебраической системы – решетку.

Пусть дано частично-упорядоченное множество М. Отношение порядка в общем случае будем обозначать .Верхней гранью элементов а и b из М называется элемент , такой чтои.Нижней гранью элементов а и b из М называется элемент, такой чтои. В общем случае для некоторых элементова и b нижняя грань может не существовать или не быть единственной.

Решеткой называется частично упорядоченной множество, в котором для любых двух элементов а и b существует и единственна наибольшая нижняя грань, обозначаемая инаименьшая верхняя грань, обозначаемая . Таким образом решетка – это алгебраическая система видас одним бинарным отношением и одной бинарной операцией.

Пример 4.

Любое полностью упорядоченное множество (например, множество целых чисел) можно превратить в решетку, определив для любых а и b из М ;.

Упражнения

1. Проверить коммутативность и ассоциативность операций.

1) сложение чисел; 2) умножение чисел; 3) сложение матриц; 4) умножение матриц (проверить на примере квадратных матриц А, В и С 2-ого порядка); 5) возведение в степень; 6)  ln xy (где х, у >0); 7) х-у; з) х/у.

2. Проверить дистрибутивность слева и справа операции ψ отношению к операции φ.

1) φ – сложение чисел, ψ – умножение чисел; 2) φ – умножение чисел, ψ – сложение чисел; 3) φ – объединение множеств, ψ – пересечение множеств; 4)  φ – пересечение множеств, ψ – объединение множеств; 5) φ – умножение чисел, ψ – возведение в степень; 6)  φ – возведение в степень, ψ – умножение чисел; 7) φ – возведение в степень, ψ – сложение чисел.

3. На множестве задать с помощью таблицы Келли операции– сложение по модулю 4 и– умножение по модулю 4. Продемонстрировать на примере их коммутативность, ассоциативность, дистрибутивностьпо отношению к, отсутствие дистрибутивностипо отношению к.

4. На множестве задать с помощью таблицы Келли операции – сложение по модулю 16 и– умножение по модулю 16.

Найти значения выражений:

1) ;

2) .

5. В конечной алгебре поля рассчитать значения выражений:

1) ;

2) .

6. В поле , операции которого заданы таблицами Келли

*	a	b	c	d		+	a	b	c	d
a	a	a	a	a		a	a	b	c	d
b	a	b	c	d		b	b	a	d	c
c	a	c	d	b		c	c	d	a	b
d	a	d	b	c		d	d	c	b	а

1) единичный элемент по операции * ;

2) единичный элемент по операции + ;

3) противоположный и обратный элемент для каждого элемента ;

4) найти значения выражений:

а) ;

б) ;

в) .

5) решить систему

;

.

7. Дано множество . Задано поле, где

	a	b	c	d		+	a	b	c	d
a	a	a	a	a		a	a	b	c	d
b	a	b	c	d		b	b	a	d	c
c	a	c	d	b		c	c	d	a	b
d	a	d	b	c		d	d	c	b	а

Найти единичные элементы по операциям и +, противоположные элементы для каждого, решить систему:

;

.

8. Доказать единственность единичного элемента в группе.

9. Доказать единственность обратного элемента в группе.

10. Пусть ассоциативная операция, заданная на множестве А, такая что для каждого элементасуществует обратный элемент.Доказать, что .

11. Дано . На множестве А заданы преобразования. На множестве преобразований задана операция композиции преобразований.

Проверить, будет ли алгебра полугруппой.

12. Составить полугруппу с операцией – композиция преобразований, для которой множество подстановокявляется системой образующих.

Что надо сделать, чтобы эта полугруппа стала моноидом.

13. Пусть S – множество всех перестановок . Определить свойства алгебры. Будет ли оно группой? Будет ли группа абелевой?

14. Будет ли алгебра (B(U), ) решеткой? Изобразить диаграмму Хасса.

15. Будет ли алгебра () решеткой? Изобразить диаграмму Хасса.

16. Является ли решеткой множество целых чисел Z с операциями и, таких что для любыхвыполняется:

, .

17. Будет ли решеткой множество, диаграмма Хасса которой изображена на рисунке. Почему?

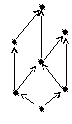
Рис. 1 Рис. 2 Рис. 3

18. Проверить на примере выполнение условия изоморфизма между алгебрами:

1) (B(U), , ­┐) и (, ┐);

2) (, ┐); (B (U), , ­┐) , где.

19. Определить изоморфны ли алгебры:

1) и, где гомоморфизм задается;

2) и, где гомоморфизм задается;

3) и, где гомоморфизм задается ;

4) и , где гомоморфизм задается ;

5) и, где гомоморфизм задается;

6) и, где гомоморфизм задается;

7) и, где гомоморфизм задается;