
- •Глава I. Линейные операторы в евклидовом и унитарном пространствах.
- •§1.1. Евклидовы и унитарные пространства.
- •§1.2. Изоморфизм унитарных пространств.
- •§1.3. Линейные функции.
- •§1.4. Сопряжённые операторы.
- •§1.5. Нормальные операторы.
- •§1.6. Унитарные операторы.
- •§1.7. Эрмитовы (самосопряжённые) операторы.
- •§1.8. Кососимметрические операторы.
- •§1.9. Неотрицательные линейные операторы.
- •§1.10. Линейные операторы в евклидовом пространстве.
- •Глава II. Квадратичные формы.
- •§2.1. Приведение квадратичной формы к каноническому виду.
- •§2.2. Приведение квадратичной формы к главным осям.
- •§2.3. Закон инерции.
- •§2.4. Распадающиеся квадратичные формы.
- •§2.5. Положительно определенные формы.
- •§2.6. Пары форм.
- •Глава III. Жорданова нормальная форма матрицы.
- •§3.1. Матрицы, их эквивалентность.
- •§3.2. Унимодулярные -матрицы.
- •§3.3. Матричные многочлены.
- •§3.4. Связь подобия числовых матриц с
- •§ 3.5. Жорданова нормальная форма.
- •§ 3.6. Приведение матрицы к жордановой нормальной форме.
- •§ 3.7. Минимальный многочлен.
- •Глава I. Линейные операторы в евклидовом
§2.2. Приведение квадратичной формы к главным осям.
Теория приведения
квадратичной формы к каноническому
виду, изложенная в предыдущем параграфе,
построена по аналогии с геометрической
теорией центральных кривых второго
порядка, но не может считаться обобщением
этой последней теории. В самом деле, в
нашей теории допускается использование
любых невырожденных линейных
преобразований, в то время как приведение
кривой второго порядка к каноническому
виду достигается применением линейных
преобразований весьма специального
вида (2), являющихся вращениями плоскости.
Эта геометрическая теория может быть,
однако, обобщена на случай квадратичных
форм от
![]() неизвестных с действительными
коэффициентами, если потребовать, чтобы
матрица преобразования
неизвестных с действительными
коэффициентами, если потребовать, чтобы
матрица преобразования![]() была ортогональной. Такое преобразование
называетсяортогональным,
а сама процедура
была ортогональной. Такое преобразование
называетсяортогональным,
а сама процедура
![]() приведением
квадратичных форм к главным осям.
приведением
квадратичных форм к главным осям.
ТЕОРЕМА. Каждая квадратичная форма некоторым ортогональным преобразованием может быть приведена к каноническому виду.
ДОКАЗАТЕЛЬСТВО.
Будем смотреть на матрицу квадратичной
формы как на матрицу некоторого линейного
оператора в евклидовом пространстве.
Если
![]() матрица квадратичной формы, то она
симметрическая порядка
матрица квадратичной формы, то она
симметрическая порядка![]() .
Если
.
Если![]() некоторый ортонормированный базис
некоторый ортонормированный базис![]() мерного
евклидова пространства, то матрица
мерного
евклидова пространства, то матрица![]() задаёт в этом базисе симметрический
оператор
задаёт в этом базисе симметрический
оператор![]() .
По основной теореме о симметрических
операторах в евклидовом пространстве
в подходящем ортонормированном базисе
.
По основной теореме о симметрических
операторах в евклидовом пространстве
в подходящем ортонормированном базисе![]() его матрица
его матрица![]() будет диагональной. Пусть
будет диагональной. Пусть![]() матрица перехода от
матрица перехода от![]() к
к![]() ,
тогда
,
тогда![]() .
.
Но матрица
![]() ,
как матрица перехода от одного
ортонормированного базиса к другому,
по теореме 2§1.6
будет ортогональной, а значит,
,
как матрица перехода от одного
ортонормированного базиса к другому,
по теореме 2§1.6
будет ортогональной, а значит,
![]() .
Поэтому
.
Поэтому
![]() .
А именно так преобразуется матрица
.
А именно так преобразуется матрица
![]() квадратичной формы, подвергнутой
линейному преобразованию неизвестных
с матрицей
квадратичной формы, подвергнутой
линейному преобразованию неизвестных
с матрицей![]() .
.
Итак, преобразование
неизвестных, имеющее матрицу
![]() ортогонально, а матрица
ортогонально, а матрица![]() ,
будучи диагональной, соответствует
квадратичной форме канонического вида.
□
,
будучи диагональной, соответствует
квадратичной форме канонического вида.
□
Тот факт, что
матрица линейного оператора
![]() в базисе, составленном из собственных
векторов, имеет диагональный вид (с
собственными значениями по главной
диагонали) [2], даёт нам метод практического
отыскания канонического вида квадратичной
формы, а также самого этого ортогонального
преобразования.
в базисе, составленном из собственных
векторов, имеет диагональный вид (с
собственными значениями по главной
диагонали) [2], даёт нам метод практического
отыскания канонического вида квадратичной
формы, а также самого этого ортогонального
преобразования.
Пример 2. Найти ортогональное преобразование, приводящее квадратичную форму
![]()
к каноническому виду и написать этот канонический вид.
Решение. Матрица этой формы имеет вид
 ,
,
Найдём её характеристический многочлен:
 .
.
Таким образом,
матрица
![]() имеет двукратный корень
имеет двукратный корень![]() и простой корень
и простой корень![]() .
Следовательно, канонический вид данной
квадратичной формы будет
.
Следовательно, канонический вид данной
квадратичной формы будет
![]() .
.
Найдём ортогональное
преобразование, осуществляющее это
приведение. Для этого найдём собственные
векторы, соответствующие найденным
собственным значениям
![]() ,
т. е. решим системы линейных однородных
уравнений
,
т. е. решим системы линейных однородных
уравнений![]() для каждого
для каждого![]() .
.
При
![]() имеем
имеем
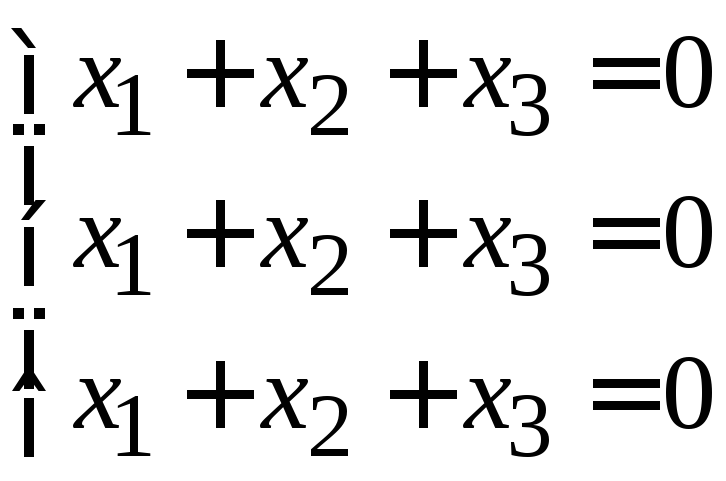 .
.
Откуда
![]() ,
т. е. имеются 2 независимые переменные,
и фундаментальный набор решений будет:
,
т. е. имеются 2 независимые переменные,
и фундаментальный набор решений будет:
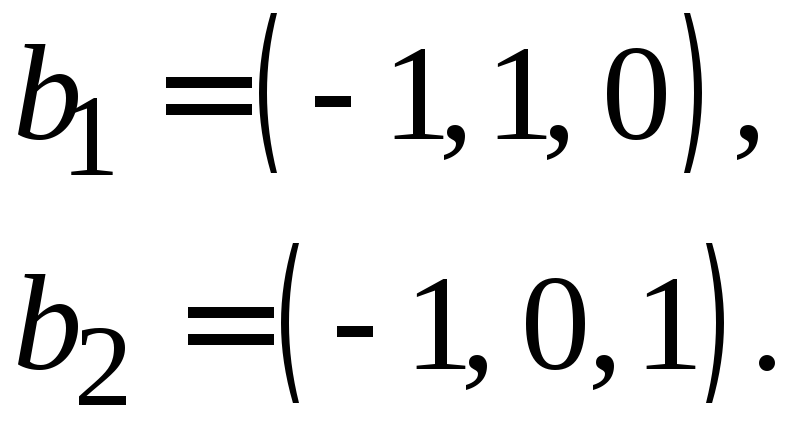
Применив к ним процесс ортогонализации, получим:
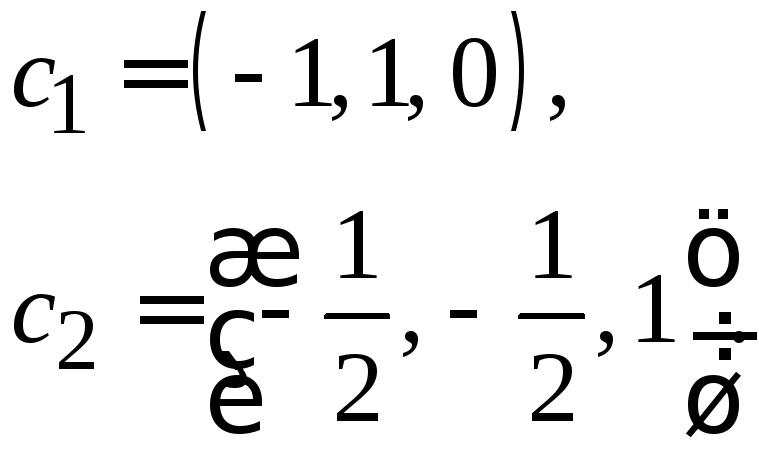
При
![]() имеем
имеем
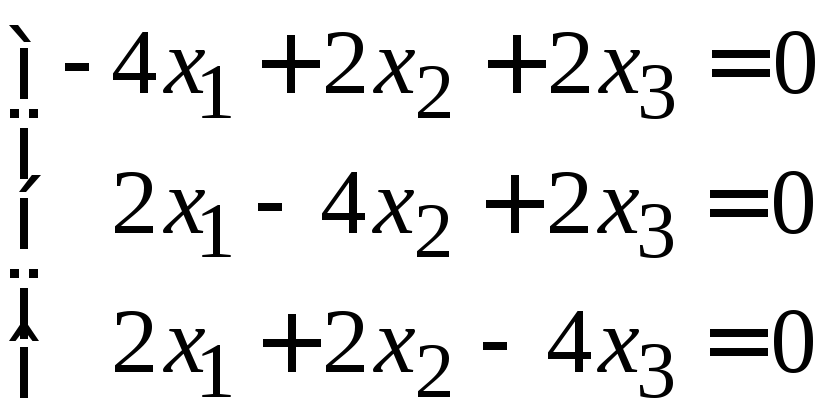 .
.
Данная система эквивалентна следующей:
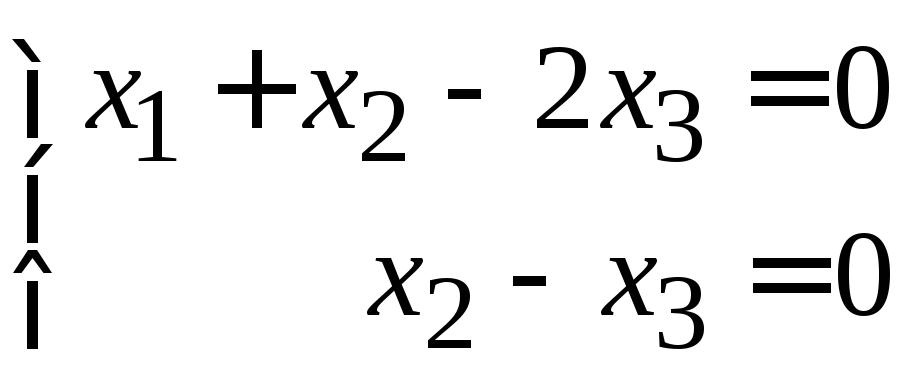 ,
,
решением которой будет
![]() .
.
Остаётся нормировать
систему
![]() :
:

Таким образом искомое преобразование имеет вид:
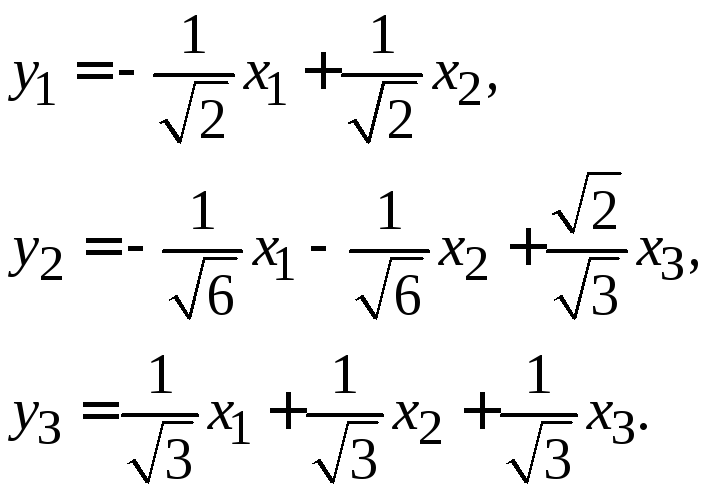
![]()
Для того чтобы
найти матрицу преобразования
![]() ,
нужно выразить переменные
,
нужно выразить переменные![]() через
через![]() ,
т. е. найти матрицу, обратную матрице
преобразования
,
т. е. найти матрицу, обратную матрице
преобразования![]() .
А так как
.
А так как
![]() ,
то достаточно транспонировать матрицу
преобразования
,
то достаточно транспонировать матрицу
преобразования
![]() .
Окончательно имеем:
.
Окончательно имеем:
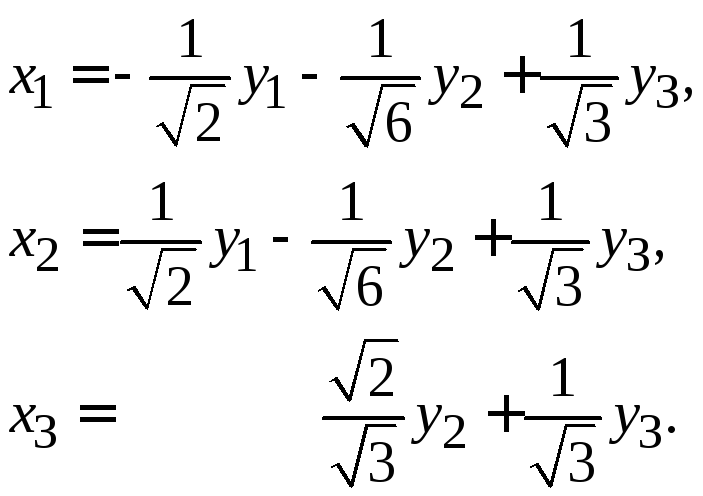 .
.
