§1.10. Линейные операторы в евклидовом пространстве.
Как уже отмечалось в §1.4 (теорема 3), в унитарном пространстве всякий линейный оператор имеет собственный вектор (одномерное инвариантное подпространство). В случае евклидова пространства это утверждение неверно. Однако имеет место следующая
ТЕОРЕМА
1. У
всякого линейного оператора
в евклидовом пространстве
существует одномерное или двумерное
инвариантное подпространство.
ДОКАЗАТЕЛЬСТВО.
Выберем в
базис
.
Оператору
в этом базисе соответствует матрица
.
Рассмотрим систему уравнений
(1)
и будем искать для
нее ненулевое решение
.
Такое решение существует тогда и только
тогда, когда определитель
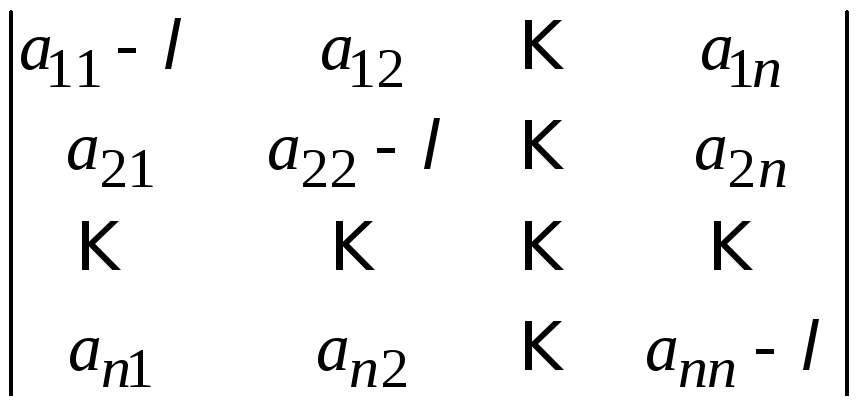
равен нулю. Приравняв
его нулю, мы получим уравнение
ой
степени относительно
с действительными коэффициентами. Пусть
есть корень этого уравнения. Возможны
два случая:
a) 
есть вещественный корень этого уравнения.
Тогда можно найти вещественные не все
равные нулю числа
,
являющиеся решением системы (1). Считая
их координатами некоторого вектора
в базисе
,
мы можем систему (1) переписать в виде
(где
столбец из координат вектора
)
или
,
т. е.
порождает
одномерное инвариантное подпространство.
b) 
,
т. е.
комплексно. Пусть
есть решение
системы (1), подставляя эти числа вместо
в(1)
и отделяя
вещественную часть от мнимой, получим:
(2)
и соответственно
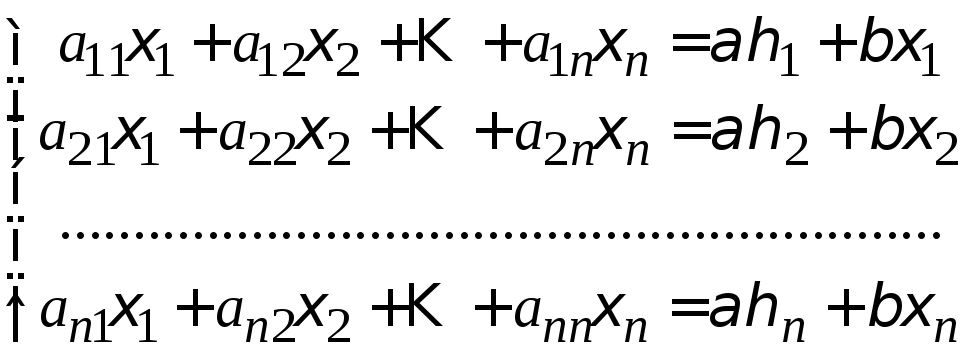(2')
Будем теперь
(соответственно
)
считать координатами некоторого вектора
(соответственно
)
в
,
тогда соотношения
(2) и (2') можно записать следующим образом:
(3)
Равенства (3)
означают, что двумерное подпространство,
порожденное векторами
и
,
инвариантно относительно
.
□
Если потребовать
в доказательстве теоремы, чтобы базис
был ортонормированным, а оператор
нормальным, то векторы
и
будут ортогональными. Действительно,
если
собственное значение, то и
также будет собственным значением (как
корни многочлена с действительными
коэффициентами). Соответствующие
собственные векторы
,
будут ортогональными
(теорема 2 §1.4).
Тогда
.
Следовательно,
.
Докажем теперь,
что подпространство векторов
,
ортогональных векторам
и
,
инвариантно, относительно оператора
.
Оно является пересечением двух
подпространств, ортогональных собственным
векторам нормального оператора. Если
,
т. е.
,
то
.
Аналогично,
.
Рассмотрим
ограничение
оператора
в двумерном подпространстве, порождённом
векторами
и
из доказательства предыдущей теоремы.
Матрица
оператора
в базисе
будет:
.
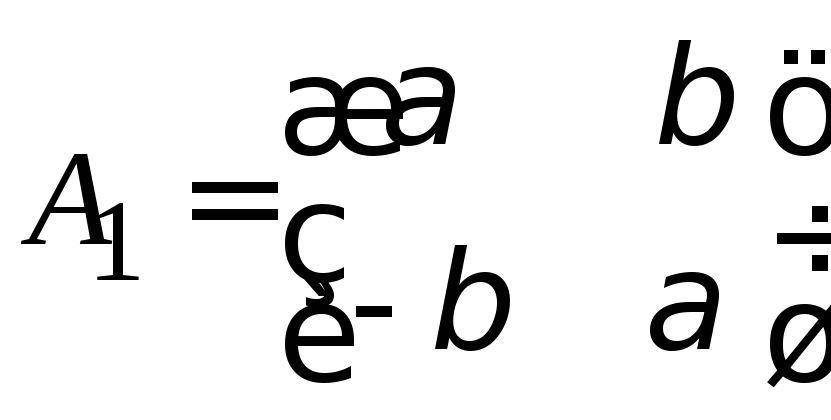Представляя
комплексное число
в тригонометрической форме
,
придадим матрице
следующий вид
.
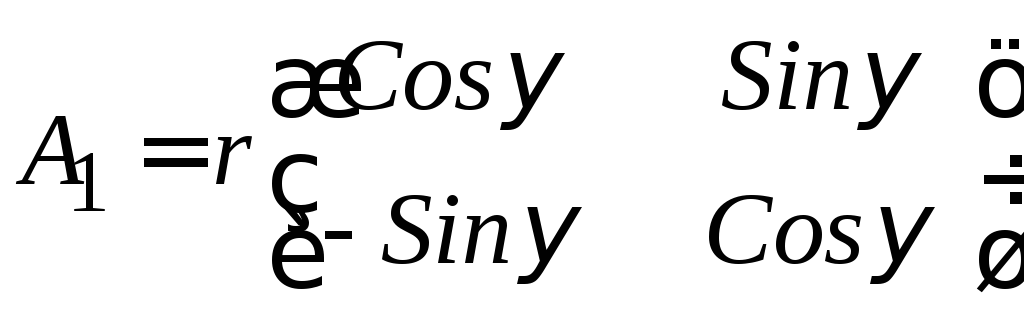Таким образом,
оператор
есть композиция операторов с матрицами
и
.
Первый из которых
соответствует преобразованию подобия
с центром в начале координат и коэффициентом
растяжения
;
второй
поворот в плоскости
на угол
около начала координат.
ТЕОРЕМА 2. (основная
о нормальных операторах в евклидовых
пространствах). Матрица
нормального оператора
в евклидовом пространстве имеет
клеточно-диагональный вид в подходящем
ортонормированном базисе. В клетках
порядка 1 находятся действительные
числа, а клетки порядка 2 имеют вид
.
ДОКАЗАТЕЛЬСТВО.
Оно аналогично доказательству теоремы
3 §1.4
о нормальных операторах. Отличие состоит
в том, что мы не можем утверждать, что
характеристический многочлен
всегда имеет действительный корень. Но
тогда он имеет 2 комплексно-сопряжённых
корня
и
,
которые по теореме 1 позволяют определить
подпространство размерности 2, инвариантное
относительно
,
которое порождено двумя ортогональными
векторами
и
.
Клетка матрицы ограничения
оператора
в базисе
имеет вид
.
Так как пространство
векторов, ортогональных векторам
и
так
же инвариантно относительно
,
то осталось воспользоваться индукцией
по размерности пространства. □
ТЕОРЕМА 3. (основная
об ортогональных операторах в евклидовых
пространствах). В
подходящем ортонормированном базисе
матрица ортогонального оператора
клеточно-диагональная с клетками порядка
1 и 2; причём в клетках порядка 1 содержатся
числа 1 или -1, а клетки порядка 2 имеют
вид
,
.
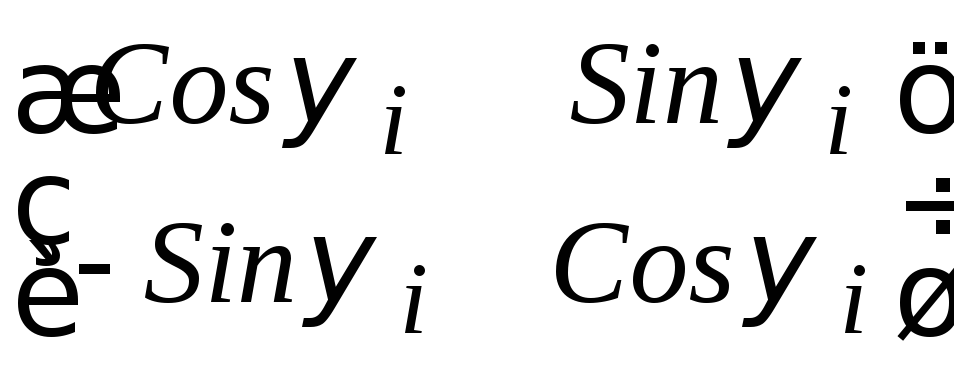ДОКАЗАТЕЛЬСТВО.
Оно следует из теоремы 2 о нормальных
операторах в евклидовых пространствах
и того факта, что собственные значения
ортогонального оператора (как частного
случая унитарного оператора) по модулю
равны 1. Действительно, если модули
собственных значений чисел
и
равны 1, то в тригонометрической форме
и клетка
имеет вид
.
□
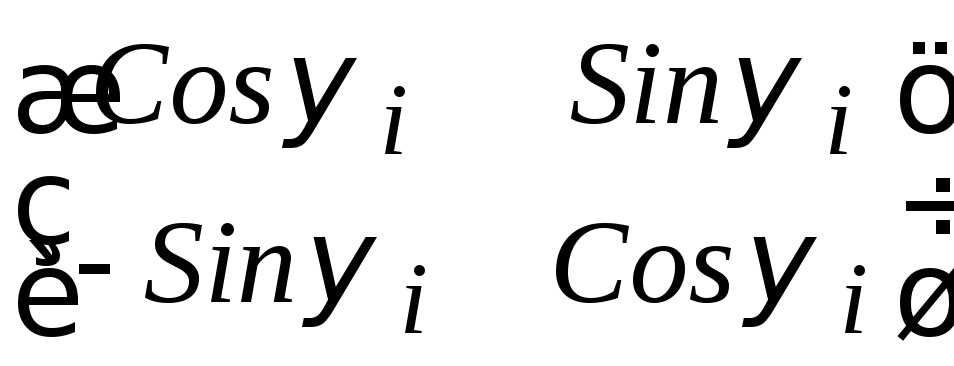Пример 3. Рассмотрим
трёхмерное евклидово пространство
.
По теореме 3 для каждого ортогонального
оператора
пространства
можно найти такую ортонормированную
систему векторов
,
что матрица оператора
будет иметь один из следующих шести
видов:
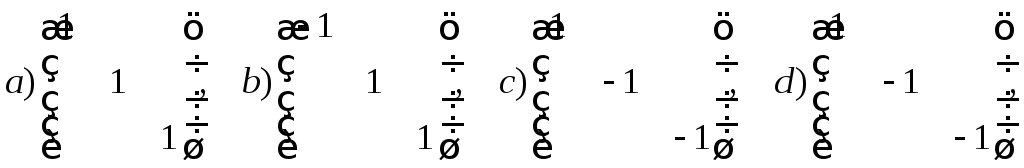
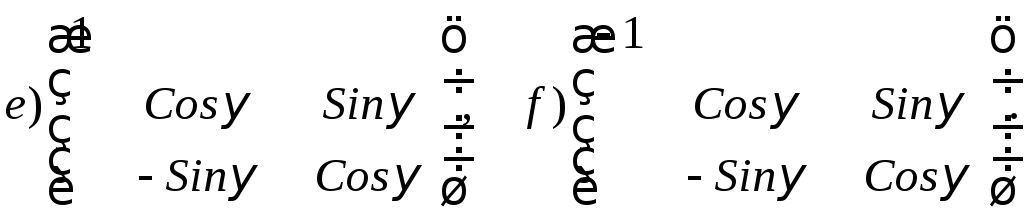
Операторы соответствуют следующим преобразованиям пространства:
тождественное преобразование;
зеркальное отображение относительно плоскости
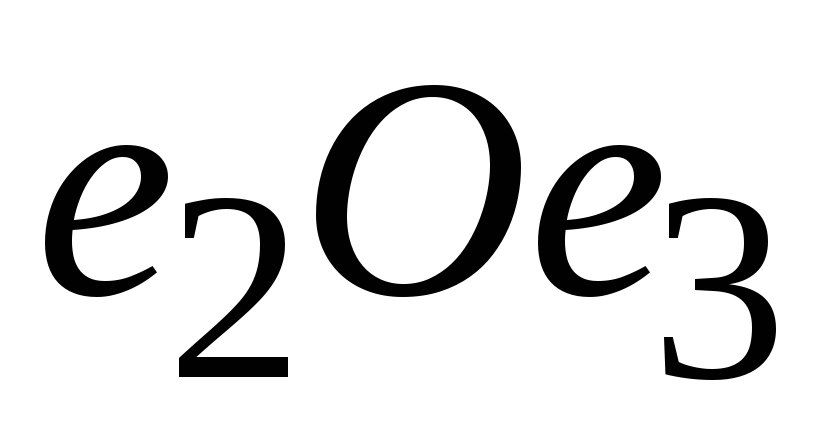;зеркальное отображение относительно прямой
;зеркальное отображение относительно точки
;вращение на угол
около оси
;вращение на угол
около оси
,
сопровождаемое зеркальным отображением
относительно плоскости
.
Для симметрических
операторов теорема формулируется так
же, как и для эрмитовых. Согласно теореме
2 данного параграфа матрица оператора
распадается на клетки порядков 1 или 2.
При этом клетки порядка 2 появляются
только тогда, когда характеристический
многочлен оператора имеет комплексные
корни. Но характеристические корни
симметрических операторов действительны.
Следовательно, справедлива
ТЕОРЕМА 4. (основная о симметрических операторах). Матрица симметрического оператора в подходящем ортонормированном базисе является диагональной с действительными числами по главной диагонали. □
ТЕОРЕМА 5. (основная
о кососимметрических операторах в
евклидовых пространствах). В
подходящем ортонормированном базисе
матрица кососимметрического оператора
евклидова пространства имеет
клеточно-диагональный вид с клетками
порядков 1 или 2; причём в клетках порядка
1 находится число 0, а клетки порядка 2
имеют вид
.
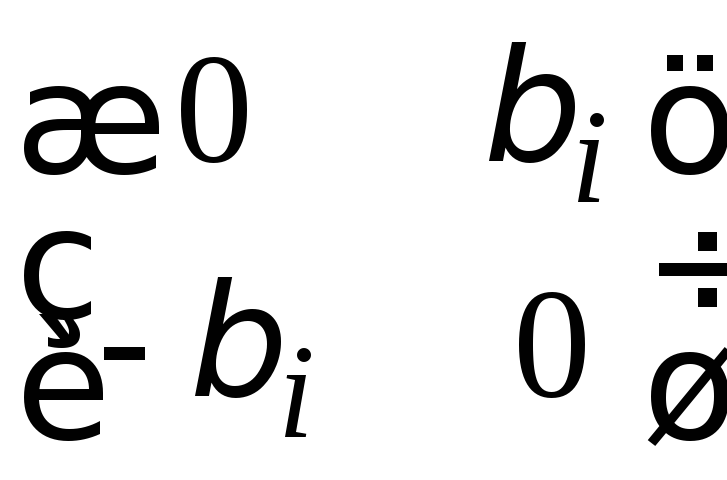ДОКАЗАТЕЛЬСТВО следует из теоремы 2 о нормальных операторах в евклидовых пространствах и того факта, что собственные значения кососимметрического оператора либо 0, либо чисто мнимое число. □
ЗАДАЧИ К ГЛАВЕ I.
1. Выяснить, являются ли ортогональными в евклидовом пространстве следующие системы векторов:
а)
;
б)
;
в)
;
г)
;
д)
?
2. Установить,
образует ли каждая из указанных систем
векторов ортогональный базис в евклидовом
пространстве
:
а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
?
3. Является ли
нормированным каждый из векторов
евклидова пространства
:
а)
б)
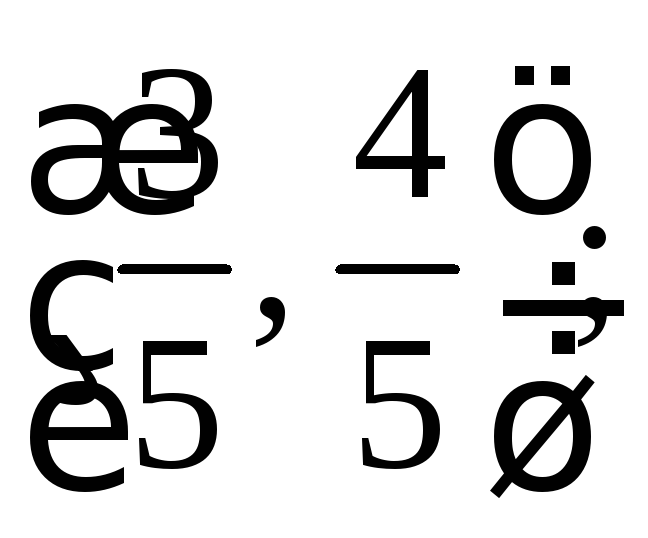
в)
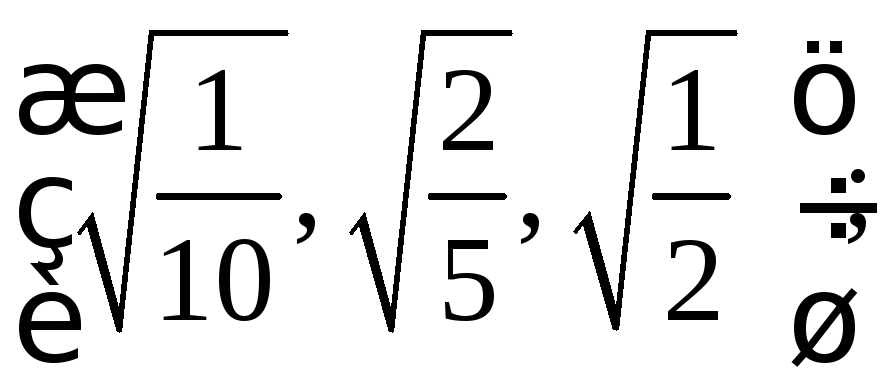
г)
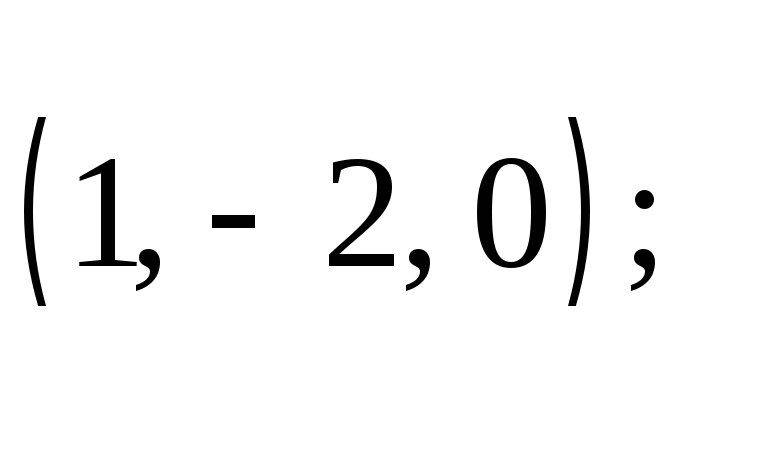
д)
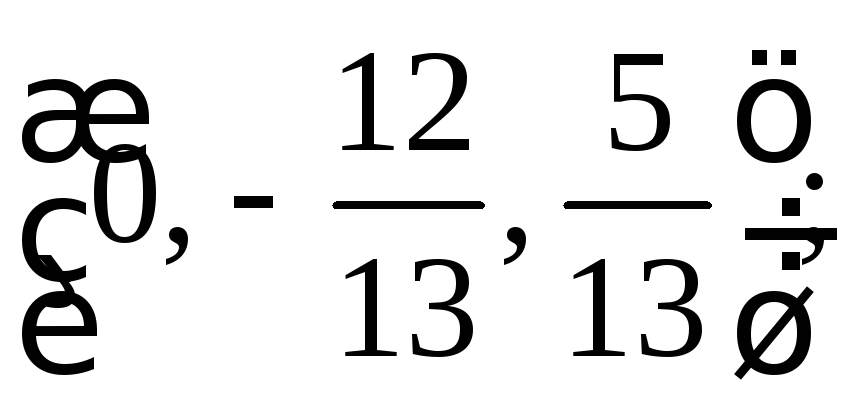
е)
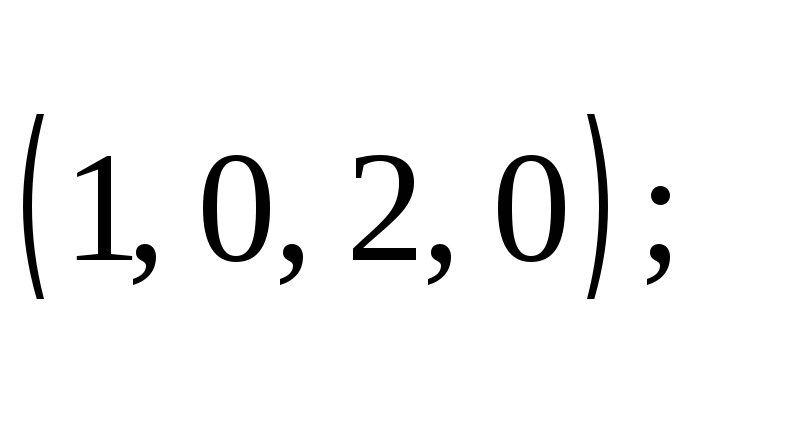
ж)
?
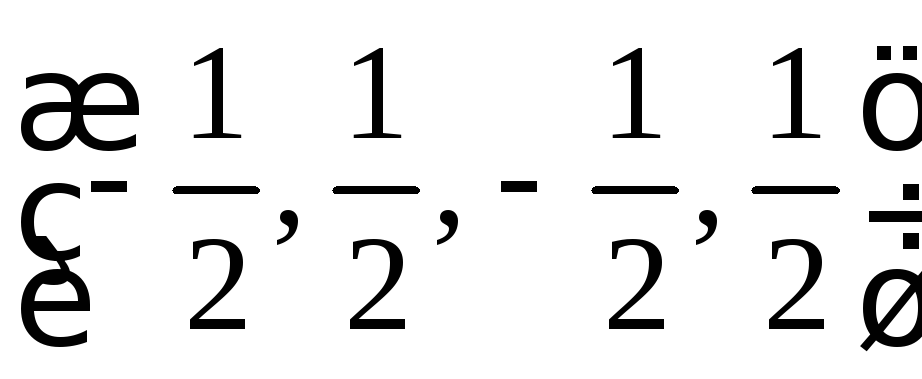4. Применяя процесс
ортогонализации, по данному базису
евклидова пространства
,
построить ортонормированный:
а)
;
б)
;
в)
.
5. Применяя процесс
ортогонализации, по данному базису
евклидова пространства
,
построить ортонормированный:
а)
;
б)
.
6. Даны векторы
евклидова пространства
.
Найти длины векторов
и
,
их скалярное произведение, косинус
угла между ними:
а)
;
б)
;
в)
.
7. Выяснить, является
ли матрица
ортогональной, и если является, то найти
обратную ей:
а)
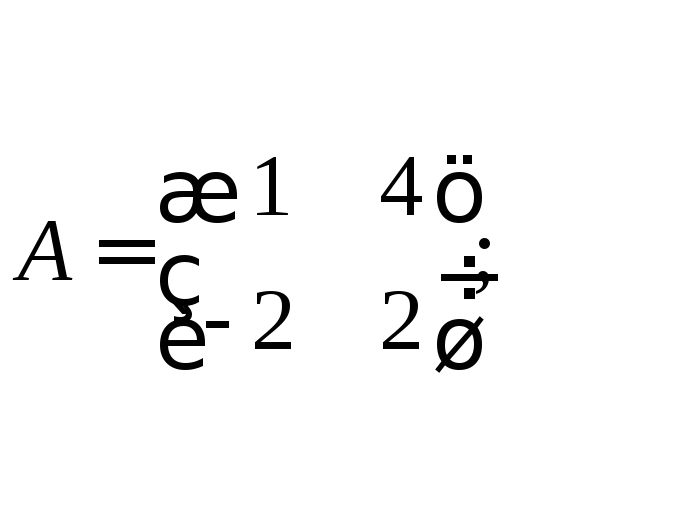
б)
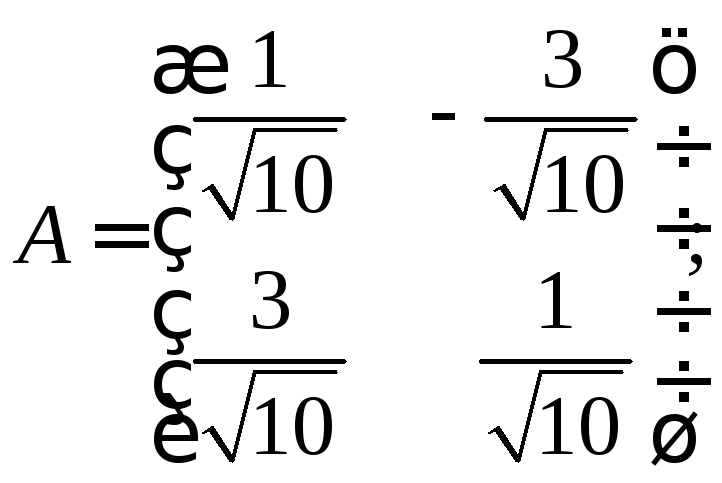
в)
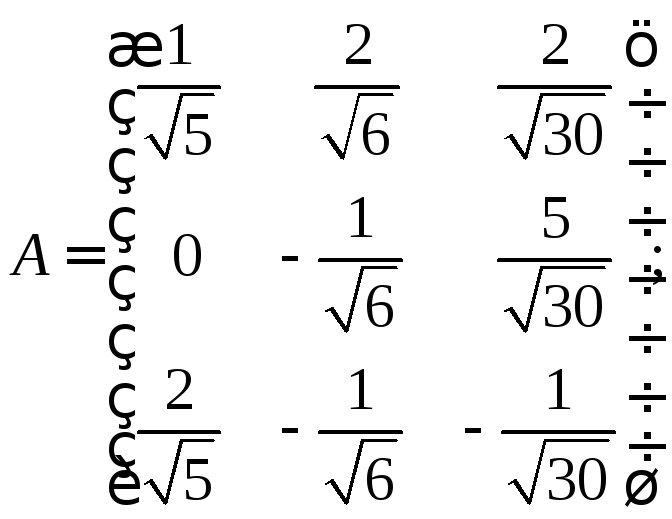
г)
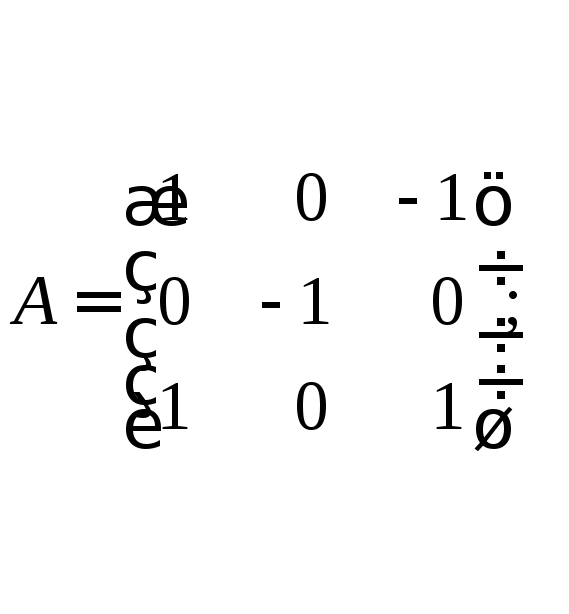
д)
е)
8. Какому условию
должны удовлетворять
и
,
чтобы матрица
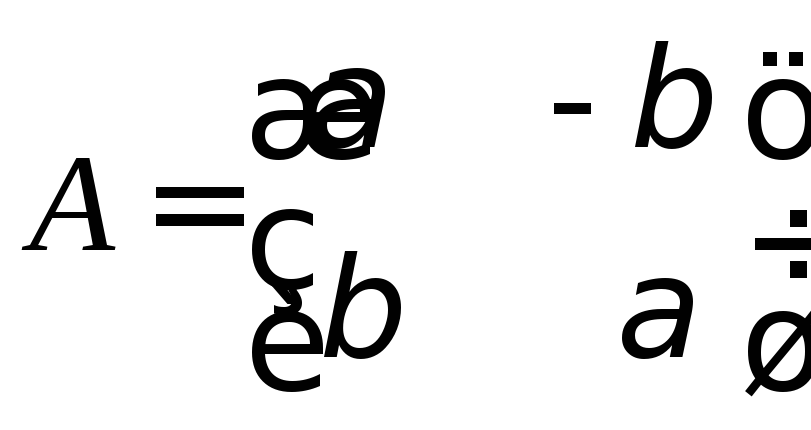была ортогональной?
9. Оператор
в некотором ортонормированном базисе
задан матрицей
.
Выяснить, является ли оператор
ортогональным, если:
а)
б)
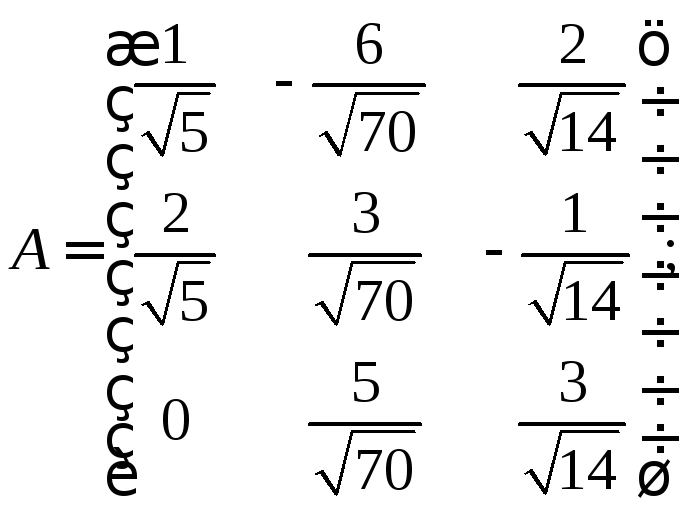
в)
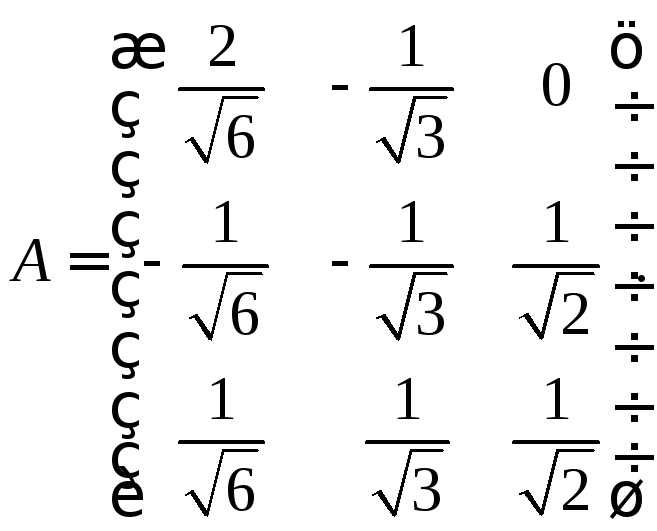
10. При каких условиях диагональная матрица будет ортогональной?
11. Оператор
имеет в некотором ортонормированном
базисе матрицу
.
Найти матрицу сопряжённого оператора
в том же базисе, если:
а)
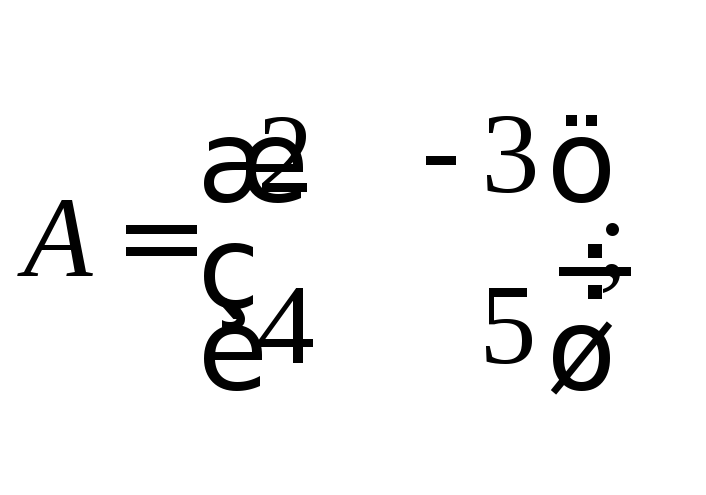
б)
в)
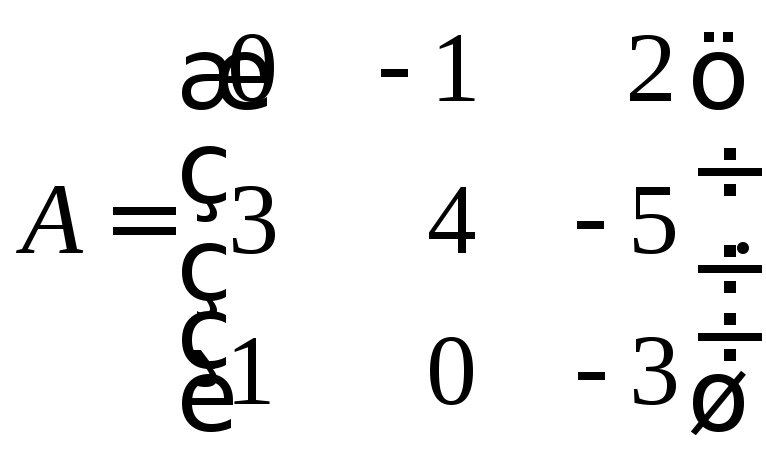
12. Оператор
имеет в некотором ортонормированном
базисе матрицу
.
Выяснить, является ли оператор
самосопряжённым, если:
а)
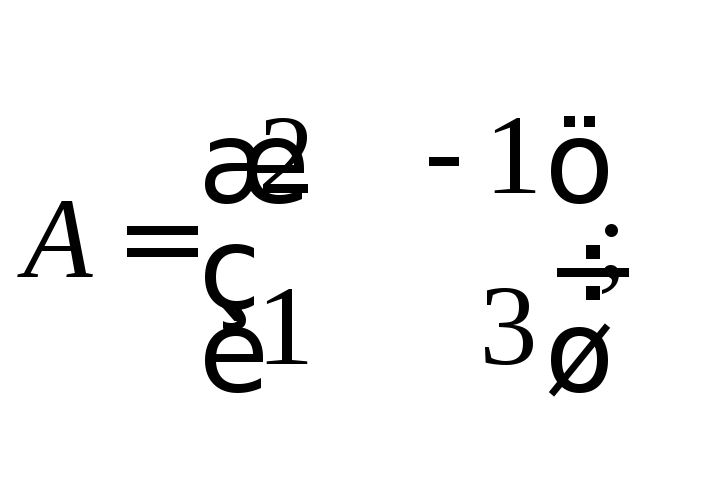
б)
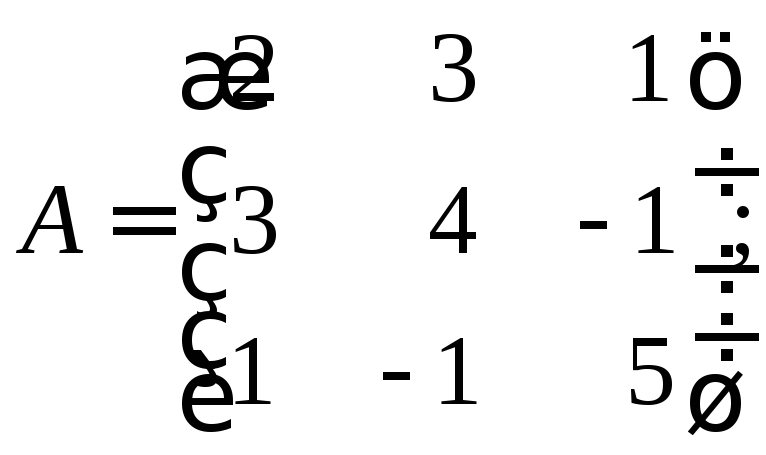
в)
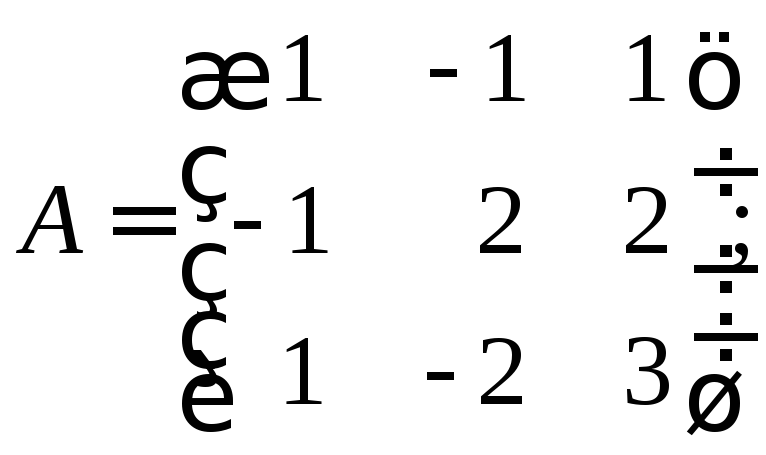
г)
13. При каком
значении
оператор, заданный матрицей
в некотором ортонормированном базисе,
является одновременно ортогональным
и самосопряжённым, если:
а)
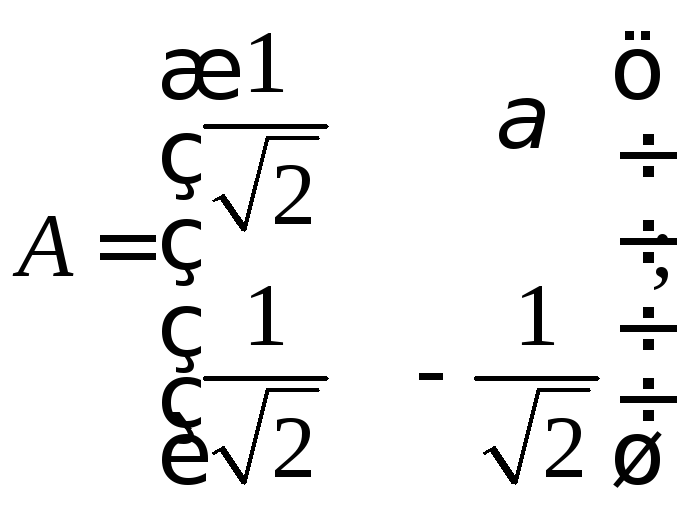
б)
14. Линейный
оператор
в некотором ортонормированном базисе
имеет матрицу
.
Найти матрицу сопряжённого оператора
в ортонормированном базисе
,
если:
а)
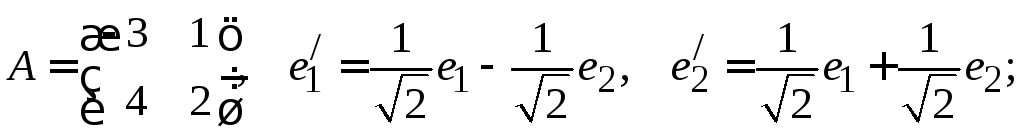
б)
в)
