
- •Глава I. Линейные операторы в евклидовом и унитарном пространствах.
- •§1.1. Евклидовы и унитарные пространства.
- •§1.2. Изоморфизм унитарных пространств.
- •§1.3. Линейные функции.
- •§1.4. Сопряжённые операторы.
- •§1.5. Нормальные операторы.
- •§1.6. Унитарные операторы.
- •§1.7. Эрмитовы (самосопряжённые) операторы.
- •§1.8. Кососимметрические операторы.
- •§1.9. Неотрицательные линейные операторы.
- •§1.10. Линейные операторы в евклидовом пространстве.
- •Глава II. Квадратичные формы.
- •§2.1. Приведение квадратичной формы к каноническому виду.
- •§2.2. Приведение квадратичной формы к главным осям.
- •§2.3. Закон инерции.
- •§2.4. Распадающиеся квадратичные формы.
- •§2.5. Положительно определенные формы.
- •§2.6. Пары форм.
- •Глава III. Жорданова нормальная форма матрицы.
- •§3.1. Матрицы, их эквивалентность.
- •§3.2. Унимодулярные -матрицы.
- •§3.3. Матричные многочлены.
- •§3.4. Связь подобия числовых матриц с
- •§ 3.5. Жорданова нормальная форма.
- •§ 3.6. Приведение матрицы к жордановой нормальной форме.
- •§ 3.7. Минимальный многочлен.
- •Глава I. Линейные операторы в евклидовом
РОССИЙСКАЯ ФЕДЕРАЦИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНСТИТУТ МАТЕМАТИКИ И КОМПЬЮТЕРНЫХ НАУК
КАФЕДРА АЛГЕБРЫ И МАТЕМАТИЧЕСКОЙ ЛОГИКИ
Д. И. ИВАНОВ
АЛГЕБРА
(ЧАСТЬ II)
Учебно-методическое пособие
Тюмень
2009
УДК 512.8
Д. И. Иванов. Алгебра (часть II): Учебно-методическое пособие по дисциплине «Алгебра» для студентов специальности «Компьютерная безопасность». Тюмень: Печатник, 2009, 125 стр.
Данное пособие разработано в соответствии с государственным образовательным стандартом и учебным планом специальности «Компьютерная безопасность» (II семестр), содержит теоретическую часть и комплекс практических заданий.
Рекомендовано к печати Учебно-методической комиссией института математики и компьютерных наук. Одобрено Учебно-методической секцией Учёного совета Тюменского государственного университета.
ОТВЕТСТВЕННЫЙ РЕДАКТОР: В. Н. Кутрунов, д. ф.-м. н., профессор.
РЕЦЕНЗЕНТЫ: А. Н. Дёгтев, д. ф.-м. н., профессор кафедры алгебры и математической логики Тюменского государственного университета.
С. Д. Захаров, к. ф.-м. н., зав. каф. математики информатики и естественных наук Тюменского государственного института мировой экономики управления и права.
© ГОУ ВПО Тюменский государственный университет, 2009
© Д. И. Иванов, 2009
Глава I. Линейные операторы в евклидовом и унитарном пространствах.
§1.1. Евклидовы и унитарные пространства.
Понятие
![]() мерного
линейного пространства
мерного
линейного пространства![]() ,
данное в § 3.1 [1], далеко не в полной мере
обобщает понятия плоскости или трехмерного
евклидова пространства: в
,
данное в § 3.1 [1], далеко не в полной мере
обобщает понятия плоскости или трехмерного
евклидова пространства: в![]() не определены ни длина вектора, ни угол
между векторами. Поэтому невозможно
развитие богатой геометрической теории.
Оказывается, что положение может быть
исправлено путем введения понятия
скалярного умножения векторов. В курсе
аналитической геометрии оно определяется
при помощи длин векторов и угла между
ними, но, как оказывается, и длина вектора,
и угол между векторами в свою очередь
могут быть выражены через скалярные
произведения. Определим поэтому в любом
не определены ни длина вектора, ни угол
между векторами. Поэтому невозможно
развитие богатой геометрической теории.
Оказывается, что положение может быть
исправлено путем введения понятия
скалярного умножения векторов. В курсе
аналитической геометрии оно определяется
при помощи длин векторов и угла между
ними, но, как оказывается, и длина вектора,
и угол между векторами в свою очередь
могут быть выражены через скалярные
произведения. Определим поэтому в любом![]() мерном
линейном пространстве понятие скалярного
умножения, причем определим аксиоматически,
при помощи некоторых свойств, которыми,
как хорошо известно, скалярное умножение
векторов плоскости или трехмерного
пространства на самом деле обладает.
мерном
линейном пространстве понятие скалярного
умножения, причем определим аксиоматически,
при помощи некоторых свойств, которыми,
как хорошо известно, скалярное умножение
векторов плоскости или трехмерного
пространства на самом деле обладает.
Будем
говорить, что в
![]() мерном
действительном линейном пространстве
мерном
действительном линейном пространстве
![]() определено
скалярное
умножение,
если всякой
паре векторов
определено
скалярное
умножение,
если всякой
паре векторов
![]() поставлено в соответствие действительное
число, обозначаемое символом
поставлено в соответствие действительное
число, обозначаемое символом![]() и называемоескалярным
произведением векторов
и называемоескалярным
произведением векторов
![]() и
и![]() ,
причем
выполняются следующие условия (здесь
,
причем
выполняются следующие условия (здесь
![]() любые
векторы
пространства
любые
векторы
пространства
![]() ,
,
![]() любое
действительное
число):
любое
действительное
число):
I. ![]()
II. ![]()
III. ![]()
IV. Если
![]() ,
то скалярный квадрат вектора
,
то скалярный квадрат вектора![]() строго положителен,
строго положителен,
![]()
Отметим, что из
III
при
![]() следует равенство
следует равенство
![]() (1)
(1)
т. е. скалярное
произведение нулевого вектора на любой
вектор
![]() равно нулю;равен
нулю, в частности, скалярный квадрат
нулевого вектора.
равно нулю;равен
нулю, в частности, скалярный квадрат
нулевого вектора.
Из II и III немедленно вытекает следующая формула для скалярного произведения и линейных комбинаций двух систем векторов:

Если в
![]() мерном
действительном линейном пространстве
определено скалярноеумножение,
то это пространство называется
мерном
действительном линейном пространстве
определено скалярноеумножение,
то это пространство называется
![]() мерным
евклидовым
пространством.
мерным
евклидовым
пространством.
УТВЕРЖДЕНИЕ 1.
При любом
![]() в
в
![]() мерном
линейном пространстве
мерном
линейном пространстве
![]() можно определить скалярное умножение,
т. е. можно превратить это пространство
в евклидово.
можно определить скалярное умножение,
т. е. можно превратить это пространство
в евклидово.
ДОКАЗАТЕЛЬСТВО.
В самом деле, возьмем в пространстве
![]() любой базис
любой базис
![]() .
Если
.
Если
![]()
то положим
![]() (2)
(2)
Легко проверяется,
что условия I
IV
будут выполнены, т. е. равенство (1)
определяет в пространстве
![]() скалярное умножение. □
скалярное умножение. □
Мы видим, что в
![]() мерном
линейном пространстве скалярное
умножение можно задать, вообще говоря,
многими различными
способами
определение (2) зависит, понятно, от
выбора базиса, а мы пока не знаем, кроме
того, нельзя ли ввести скалярное умножение
и каким-либо принципиально иным способом.
Нашей ближайшей целью является обозрение
всех возможных способов превращения
мерном
линейном пространстве скалярное
умножение можно задать, вообще говоря,
многими различными
способами
определение (2) зависит, понятно, от
выбора базиса, а мы пока не знаем, кроме
того, нельзя ли ввести скалярное умножение
и каким-либо принципиально иным способом.
Нашей ближайшей целью является обозрение
всех возможных способов превращения
![]() мерного
действительного линейного пространства
в евклидово пространство и установление
того, что в некотором смысле для всякого
мерного
действительного линейного пространства
в евклидово пространство и установление
того, что в некотором смысле для всякого![]() существует одно-единственное
существует одно-единственное![]() мерное
евклидово пространство.
мерное
евклидово пространство.
Пусть дано
произвольное
![]() мерное
евклидово пространство
мерное
евклидово пространство![]() ,
т. е. в
,
т. е. в
![]() мерном
линейном пространстве произвольным
способом введено скалярное умножение.
Векторы
мерном
линейном пространстве произвольным
способом введено скалярное умножение.
Векторы![]() и
и
![]() называются
ортогональными,
если их
скалярное произведение равно нулю,
называются
ортогональными,
если их
скалярное произведение равно нулю,
![]()
Из (1) следует, что нулевой вектор ортогонален к любому вектору; могут существовать, однако, и ненулевые ортогональные векторы.
Система векторов называется ортогональной системой, если все векторы этой системы попарно ортогональны между собой.
ТЕОРЕМА 1. Всякая ортогональная система ненулевых векторов линейно независима.
ДОКАЗАТЕЛЬСТВО.
Пусть, в самом деле, в
![]() дана система
векторов
дана система
векторов
![]() причем
причем![]() и
и
![]() (3)
(3)
Если
![]()
то, скалярно умножая
обе части этого равенства на вектор
![]() получаем:
получаем:
![]()
Отсюда, так как
![]() поIV,
вытекает
поIV,
вытекает
![]() что и требовалось доказать. □
что и требовалось доказать. □
Опишем
далее так называемый процесс
ортогонализации,
т. е. некоторый
способ перехода от любой линейно
независимой системы из
![]() векторов
векторов
![]() евклидова пространства
евклидова пространства![]() к ортогональной системе, также состоящей
из
к ортогональной системе, также состоящей
из![]() ненулевых лекторов; эти векторы будут
обозначены через
ненулевых лекторов; эти векторы будут
обозначены через![]() .
.
Положим
![]() ,
т. е. первый вектор системы (
,
т. е. первый вектор системы (![]() )
войдёт и в строящуюся нами ортогональную
систему. Положим, далее,
)
войдёт и в строящуюся нами ортогональную
систему. Положим, далее,
![]()
Так как
![]() а векторы
а векторы![]() и
и
![]() линейно независимы, то вектор
линейно независимы, то вектор![]() отличен от нуля при любом числе
отличен от нуля при любом числе![]() .
Подберем это
число из условии, что вектор
.
Подберем это
число из условии, что вектор
![]() должен быть ортогонален к вектору
должен быть ортогонален к вектору![]() :
:
![]()
откуда, ввиду IV,
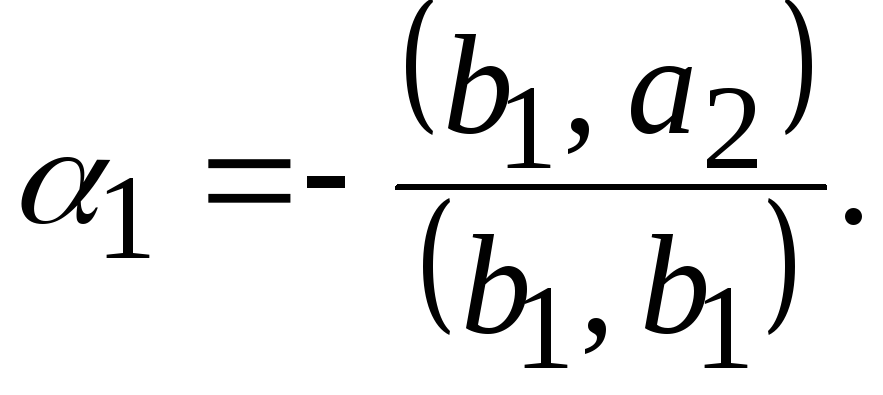
Пусть уже построена
ортогональная система ненулевых векторов
![]() ;
дополнительно предположим, что для
всякого
;
дополнительно предположим, что для
всякого![]() вектор
вектор![]() является линейной комбинацией векторов
является линейной комбинацией векторов![]() Это предположение будет выполняться
тогда и для вектора
Это предположение будет выполняться
тогда и для вектора![]() если он будет выбран в виде
если он будет выбран в виде
![]()
Вектор
![]() будет при этом отличен от нуля, так как
система (
будет при этом отличен от нуля, так как
система (![]() )
линейно независимая, а вектор
)
линейно независимая, а вектор![]() не входит в записи векторов
не входит в записи векторов![]() .
Коэффициенты
.
Коэффициенты![]() подберем из условия, что вектор
подберем из условия, что вектор![]() должен быть ортогонален ко всем векторам
должен быть ортогонален ко всем векторам![]()
![]()
отсюда, так как
векторы
![]() ортогональны между собой,
ортогональны между собой,
![]()
т. е.
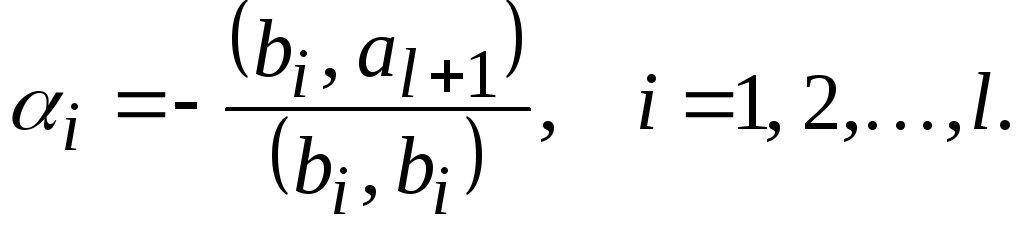
Продолжая этот
процесс, мы построим искомую ортогональную
систему
![]() .
.
Применяя процесс
ортогонализации к
произвольному
базису пространства
![]() ,
мы получим ортогональную систему из
,
мы получим ортогональную систему из![]() ненулевых векторов, т. е., так как эта
система по доказанному линейно независима,ортогональный
базис. При
этом, используя замечание, сделанное в
связи с первым шагом процесса
ортогонализации, а, также учитывая, что
всякий, ненулевой вектор можно включить
в некоторый базис пространства, можно
сформулировать даже следующее:
ненулевых векторов, т. е., так как эта
система по доказанному линейно независима,ортогональный
базис. При
этом, используя замечание, сделанное в
связи с первым шагом процесса
ортогонализации, а, также учитывая, что
всякий, ненулевой вектор можно включить
в некоторый базис пространства, можно
сформулировать даже следующее:
УТВЕРЖДЕНИЕ 2. Всякое евклидово пространство обладает ортогональными базисами, причем любой ненулевой вектор этого пространства входит в состав некоторого ортогонального базиса. □
В дальнейшем важную роль будет играть один специальный вид ортогональных базисов; базисы этого вида соответствуют прямоугольным декартовым системам координат, используемым в аналитической геометрии.
Назовем вектор
![]() нормированным,
если его
скалярный квадрат равен единице, т. е.
нормированным,
если его
скалярный квадрат равен единице, т. е.
![]()
Если
![]() ,
откуда
,
откуда
![]() ,
тонормированием
вектора
,
тонормированием
вектора
![]() называется переход к вектору
называется переход к вектору
![]()
Вектор
![]() будет нормированным, так как
будет нормированным, так как
![]()
Базис
![]() евклидова пространства
евклидова пространства![]() называетсяортонормированным,
если он
ортогонален, а все его векторы нормированы,
т. е.
называетсяортонормированным,
если он
ортогонален, а все его векторы нормированы,
т. е.
![]() (4)
(4)
Пример 1. Привести систему векторов
![]()
к ортонормированному виду.
Решение.
Применим к указанным векторам процесс
ортогонализации.
![]() Вектор
Вектор![]() ищем в виде
ищем в виде
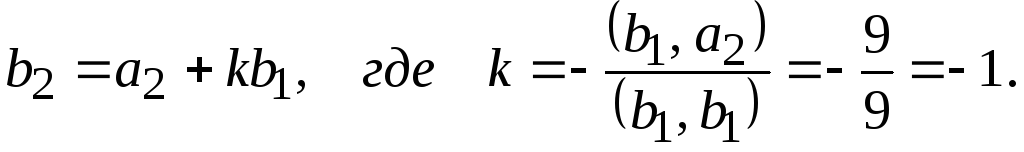 Подставляя значения,
получим
Подставляя значения,
получим
![]() Далее ищем
Далее ищем![]() Здесь
Здесь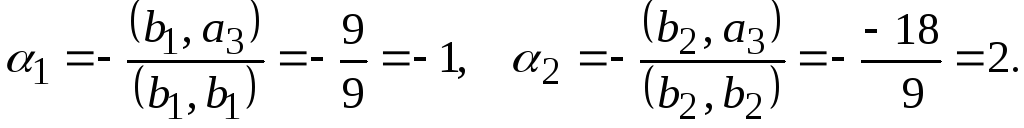 После подстановки, имеем:
После подстановки, имеем:![]()
Осталось нормировать
систему
![]() .
.
![]()
![]()
![]()
Итак,
![]() искомая ортонормированная система.
искомая ортонормированная система.
УТВЕРЖДЕНИЕ 3. Всякое евклидово пространство обладает ортонормированными базисами.
ДОКАЗАТЕЛЬСТВО.
Достаточно взять любой ортогональный
базис и нормировать все его векторы.
Базис останется при этом ортогональным,
так как при любых
![]() и
и![]() из
из![]() следует
следует
![]() □
□
ТЕОРЕМА 2. Базис
![]() евклидова пространства
евклидова пространства
![]() тогда и только тогда будет ортонормированным,
если скалярное произведение любых двух
векторов пространства равно сумме
произведений соответственных координат
этих векторов в указанном базисе, т. е.
из
тогда и только тогда будет ортонормированным,
если скалярное произведение любых двух
векторов пространства равно сумме
произведений соответственных координат
этих векторов в указанном базисе, т. е.
из
![]() (5)
(5)
следует
![]() (6)
(6)
ДОКАЗАТЕЛЬСТВО. Действительно, если для нашего базиса выполняются равенства (4), то
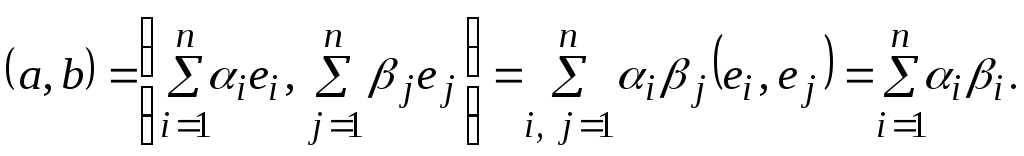
Обратно, если наш
базис таков, что для любых векторов
![]() и
и
![]() ,
записанных
в этом базисе в виде (5), справедливо
равенство (6), то, беря и качестве
,
записанных
в этом базисе в виде (5), справедливо
равенство (6), то, беря и качестве
![]() и
и![]() любые два вектора этого базиса
любые два вектора этого базиса![]() и
и![]() ,
различные или одинаковые, мы из (6) выведем
равенства (4). □
,
различные или одинаковые, мы из (6) выведем
равенства (4). □
Сопоставляя
полученный сейчас результат с изложенным
ранее доказательством существования
![]() мерных
евклидовых пространств для любого
мерных
евклидовых пространств для любого![]() ,
можно высказать следующее:
,
можно высказать следующее:
УТВЕРЖДЕНИЕ 4.
Если в
![]() мерном
линейном пространстве
мерном
линейном пространстве
![]() выбран произвольный базис, то в
выбран произвольный базис, то в![]() можно так задать скалярное умножение,
что в полученном евклидовом пространстве
выбранный базис будет одним из
ортонормированных.□
можно так задать скалярное умножение,
что в полученном евклидовом пространстве
выбранный базис будет одним из
ортонормированных.□
Евклидовы
пространства
![]() и
и
![]() называются
изоморфными,
если между
векторами этих пространств можно
установить такое взаимно однозначное
соответствие, что выполняются следующие
требования:
называются
изоморфными,
если между
векторами этих пространств можно
установить такое взаимно однозначное
соответствие, что выполняются следующие
требования:
это соответствие является изоморфным соответствием между
 и
и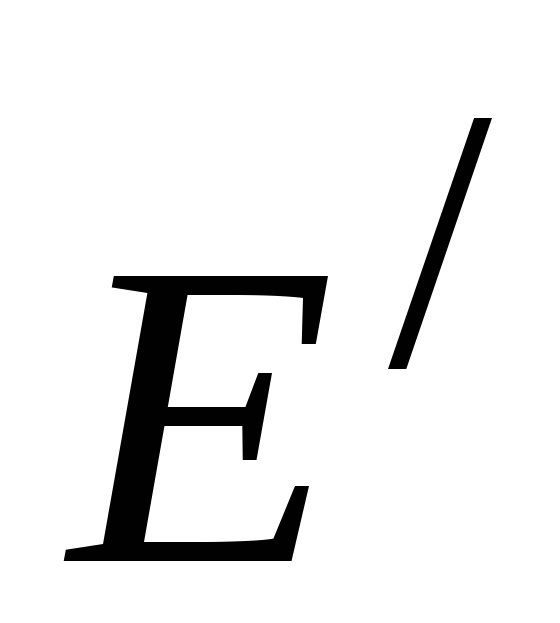 ,
рассматриваемыми как линейные
пространства;
,
рассматриваемыми как линейные
пространства;при этом соответствии сохраняется скалярное произведение; иными словами, если образами векторов
 и
и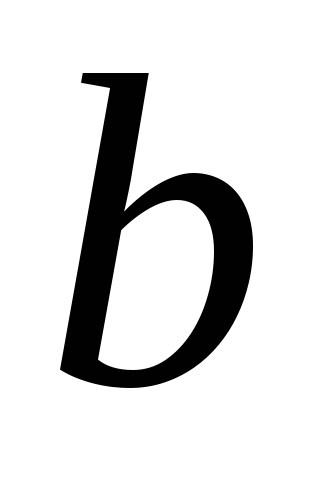 из
из служат соответственно векторы
служат соответственно векторы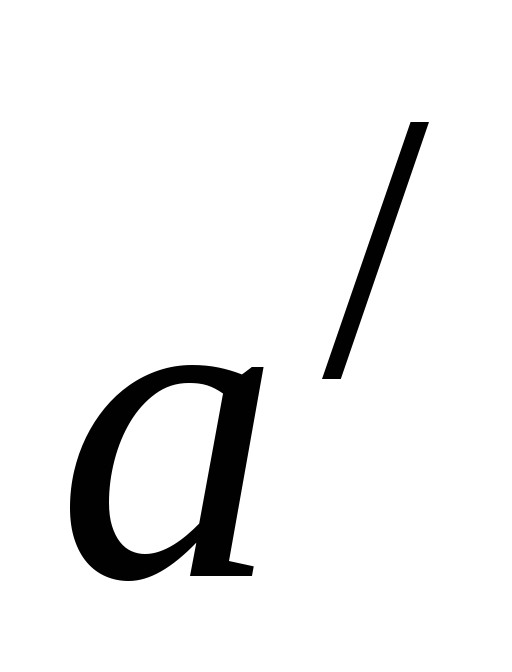 и
и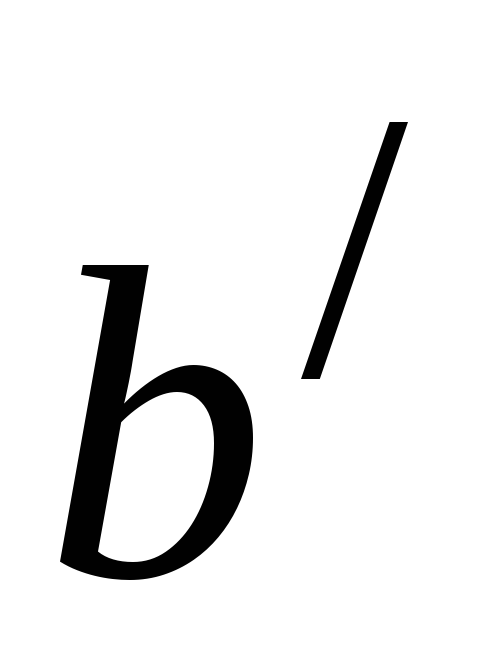 из
из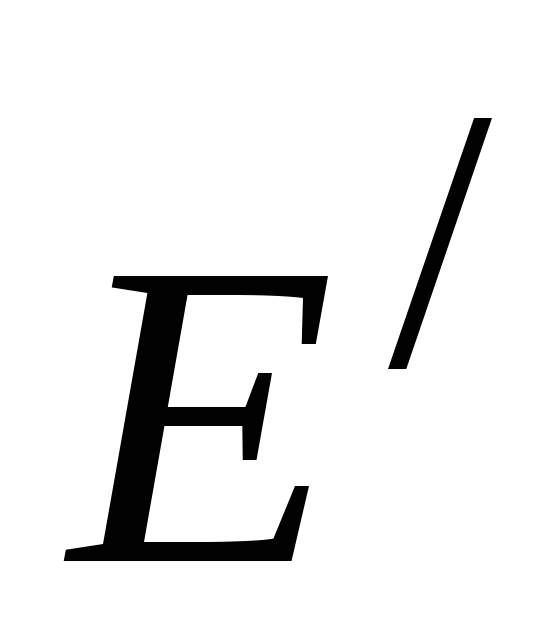 ,
то
,
то
![]() (7)
(7)
Из условия 1) сразу следует, что изоморфные евклидовы пространства имеют одну и ту же размерность. Докажем обратное утверждение:
ТЕОРЕМА 3. Любые
евклидовы пространства
![]() и
и
![]() ,
имеющие
одну и ту же размерность
,
имеющие
одну и ту же размерность
![]() ,
изоморфны между собой.
,
изоморфны между собой.
ДОКАЗАТЕЛЬСТВО.
В самом деле, выберем в пространствах
![]() и
и![]() ортонормированныебазисы
ортонормированныебазисы
![]() и, соответственно,
и, соответственно,![]() .
.
Ставя в соответствие
всякому вектору
![]() из
из![]() вектор
вектор![]() из
из![]() ,
имеющий в базисе
,
имеющий в базисе![]() те же координаты, что и вектор
те же координаты, что и вектор![]() в базисе
в базисе![]() ,
мы получим, очевидно, изоморфное
соответствие между линейными пространствами
,
мы получим, очевидно, изоморфное
соответствие между линейными пространствами![]() и
и![]() .
Покажем, что выполняется и равенство
(7): если
.
Покажем, что выполняется и равенство
(7): если
![]()
то, в силу (6):
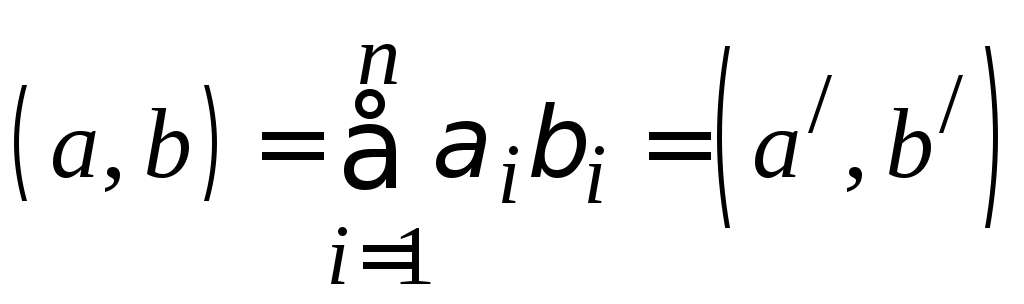 .□
.□
Естественно
изоморфные евклидовы пространства не
считать различными. Поэтому для всякого
![]() существует
единственное
существует
единственное
![]() мерное
евклидово пространство в том же смысле,
в каком для всякого
мерное
евклидово пространство в том же смысле,
в каком для всякого![]() существует единственное
существует единственное![]() мерное
действительное линейное пространство.
мерное
действительное линейное пространство.
На случай комплексных
линейных пространств понятия и результаты
настоящего параграфа переносятся
следующим образом. Комплексное линейное
пространство
![]() называется
унитарным
пространством, если
в нем задано скалярное умножение, причем
называется
унитарным
пространством, если
в нем задано скалярное умножение, причем
![]() будет комплексным
числом; при этом должны выполняться
аксиомы II
IV,
а аксиома I
заменяется следующей аксиомой:
будет комплексным
числом; при этом должны выполняться
аксиомы II
IV,
а аксиома I
заменяется следующей аксиомой:
I
'. ![]()
где черта над скалярным произведением обозначает, как обычно, переход к сопряженному комплексному числу. Следовательно, скалярное произведение в унитарном пространстве не будет коммутативным. Тем не менее, равенство, симметричное аксиоме II, остается справедливым.
II
'. ![]()
так как
![]()
III
'. ![]()
так как
![]()
IV
'. Скалярный
квадрат ненулевого вектора
![]() комплексного линейного пространства
действителен и строго положителен,
комплексного линейного пространства
действителен и строго положителен,
![]()
Понятия ортогональности
и ортонормированной системы векторов
переносятся на случай унитарных
пространств без всяких изменений. Как
и выше, доказывается существование
ортонормированных базисов во всяком
конечномерном унитарном пространстве.
При этом, однако, если
![]() ортонормированный базис и векторы
ортонормированный базис и векторы![]() имеют в этом базисе разложение
имеют в этом базисе разложение![]() ,
то
,
то
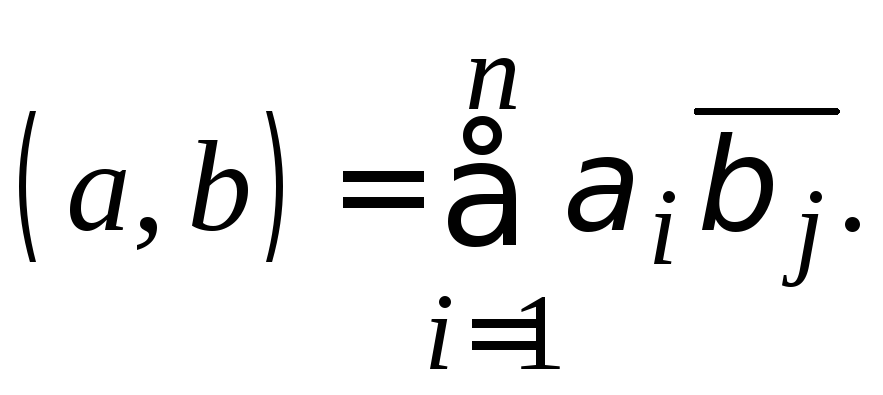
Пусть
![]() элемент унитарного пространства
элемент унитарного пространства![]() .
Число
.
Число![]()
![]() называетсядлиной
вектора
называетсядлиной
вектора
![]() в
этом пространстве.
Только нулевой вектор имеет длину,
равную нулю.
в
этом пространстве.
Только нулевой вектор имеет длину,
равную нулю.
ТЕОРЕМА 4.
Для любых
двух векторов
![]()
![]() мерного
унитарного
пространства
мерного
унитарного
пространства
![]() имеет место неравенство Коши
Буняковского
имеет место неравенство Коши
Буняковского
![]()
причем равенство
достигается лишь в случае, когда векторы
![]() и
и![]() линейно зависимые.
линейно зависимые.
ДОКАЗАТЕЛЬСТВО.
Достаточно доказать это неравенство
для векторов, отличных от нуля. Рассмотрим
![]() .
Преобразовывая левую часть, получим
.
Преобразовывая левую часть, получим
![]() .
.
Положим
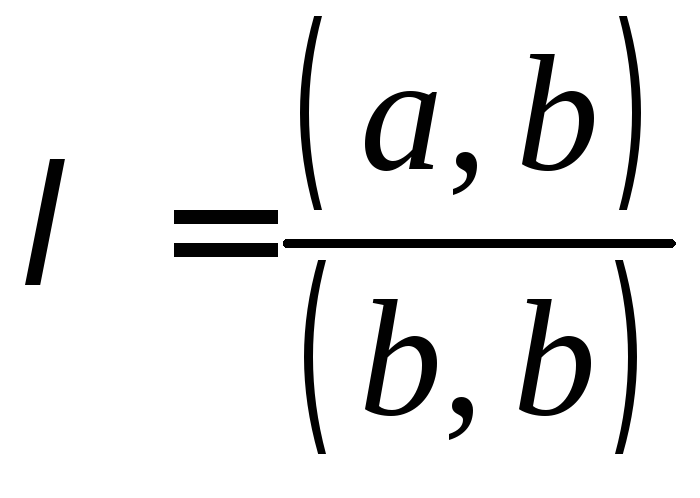 ,
после подстановки в неравенство и
домножения на
,
после подстановки в неравенство и
домножения на![]() ,
получим
,
получим
![]() .
.
Учитывая, что
![]() ,
имеем
,
имеем
![]() .
.
Если
![]() ,
т. е.
,
т. е.
![]() и
и
![]() линейно зависимые, то имеет место
равенство. Равенство достигается и в
том случае, когда один из векторов
нулевой (в этом случае система так же
линейно зависима).
□
линейно зависимые, то имеет место
равенство. Равенство достигается и в
том случае, когда один из векторов
нулевой (в этом случае система так же
линейно зависима).
□
Из неравенства Коши Буняковского легко вытекает так называемое «неравенство треугольника для векторов», а именно:
![]() .
.
Действительно,
![]() ,
,
где
![]() целая часть комплексного числа
целая часть комплексного числа![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
□
.
□
Величиной
угла между двумя отличными
от
нуля векторами
![]() и
и
![]() в
в
![]() мерномевклидовом
пространстве
называется
число
мерномевклидовом
пространстве
называется
число
![]() ,
,![]() ,
определенное условием
,
определенное условием

Из
неравенства Коши
Буняковского следует, что угол
![]() (в пределах
(в пределах
![]() )
однозначно
определен. При этом
)
однозначно
определен. При этом
![]() (т. е. векторы
(т. е. векторы![]() и
и![]() перпендикулярны или ортогональны между
собой) тогда и только тогда, когда
перпендикулярны или ортогональны между
собой) тогда и только тогда, когда
![]() .
.
