§3.3. Матричные многочлены.

Будем называть матричным многочленом порядка над полеммногочлен от, коэффициентами которого служат квадратные матрицы одного и того же порядкас элементами из поля; его общим видом будет:

(1)

Всякий матричный многочлен порядкаможно записать в видематрицы порядка. Так, например

.

И обратно, всякая матрица порядкаможет быть записана в виде матричногомногочлена порядка. Так,

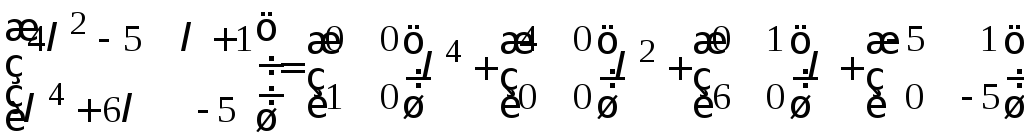
Соответствие между матрицами и матричнымимногочленами является взаимно однозначным и изоморфным. Действительно, равенствомногочленов вида (1) как матриц равносильно равенству матричных коэффициентов при одинаковых степенях, а умножение матрицы наравносильно умножению ее на числовую матрицу сна главной диагонали.

Пусть дана матрица, причем

,

где матрица не является нулевой. Числоназовемстепенью матрицы; это будет наивысшая степень (по) элементов матрицы.

Изоморфизм между матрицами и матричными многочленами позволяет развивать дляматриц теорию делимости, аналогичную теории делимости для числовых многочленов, но усложняемую некоммутативностью умножения матриц и наличием делителей нуля. Рассмотрим алгоритм деления с остатком.

ТЕОРЕМА. Пусть над полем даныматрицы порядка

,

,

причем предположим, что матрица невырожденная, т. е. существует матрица. Тогда над полемможно найти такиематрицыитого же порядка, что

, (2)

причем степень меньше степениили же. С другой стороны, над полемможно найти такиематрицыипорядка, что

, (3)

причем степень меньше степениили же. Матрицыи, а такжеи, удовлетворяющие этим условиям, определяются однозначно.

ДОКАЗАТЕЛЬСТВО этой теоремы проходит так же, как доказательство соответствующей теоремы для числовых многочленов. Пусть условию (2) удовлетворяют также матрицы и, причем степеньменьше степени . Тогда

.

Степень правой части меньше , степень же левой части, если квадратная скобка отлична от нуля, больше или равна, так как матрицаневырожденная. Отсюда следует единственность матриц и .

Докажем существование этих матриц. При степень

будет строго меньше ; обозначим её, а старший коэффициент многочленачерез. Если всё ещё, то

.

Обозначим через степень, а черезстарший коэффициент матричного многочлена. Положим затем

,

и т. д.

Так как степени многочленов ,,убывают,, то за конечное число шагов дойдём до многочлена,

,

степень которого меньше . Складывая предыдущие равенства, получим:

,

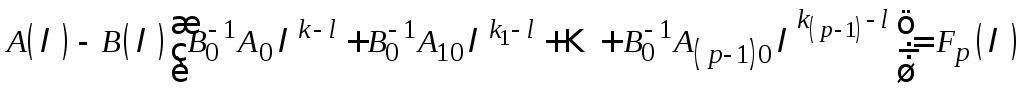где выражение в скобках и будет матричным многочленом , а .

С другой стороны, рассматривая разность

,

видим, что её степень также строго меньше , абудет старшим членом матричногомногочлена . Откуда убеждаемся, что матрицы и (а также и ), удовлетворяющие условиям теоремы, действительно в общем случае будут различными. □

§3.4. Связь подобия числовых матриц с

эквивалентностью их характеристических матриц.

Как известно [1], две квадратные матрицы порядка подобны тогда и только тогда, когда они задают один и тот же линейный оператор в разных базисах. Однако мы не можем пока ответить на вопрос, подобны ли данные числовые матрицыи(т. е. матрицы с элементами из основного поля). Тем не менее, их характеристические матрицыиявляютсяматрицами, и вопрос об эквивалентности этих матриц решается вполне эффективно. Ответ на вопрос о связи подобия числовых матриц с эквивалентностью их характеристических матриц даёт следующая

ТЕОРЕМА. Матрицы и с элементами из поля тогда и только тогда подобны, когда их характеристические матрицы и эквивалентны.

ДОКАЗАТЕЛЬСТВО. Пусть матрицы иподобны, т. е. над полемсуществует такая невырожденная матрица, что

.

Тогда

.

Невырожденные числовые матрицы иявляются, однако, унимодулярнымиматрицами. Матрицаполучена умножением матрицыслева и справа на унимодулярные матрицы, т. е..

Обратно, пусть

.

Тогда существуют такие унимодулярные матрицы и, что

. (1)

Учитывая, что для унимодулярных матриц обратные матрицы существуют и являются матрицами, выведем из (1) равенства, которые будут использованы в дальнейшем для доказательства:

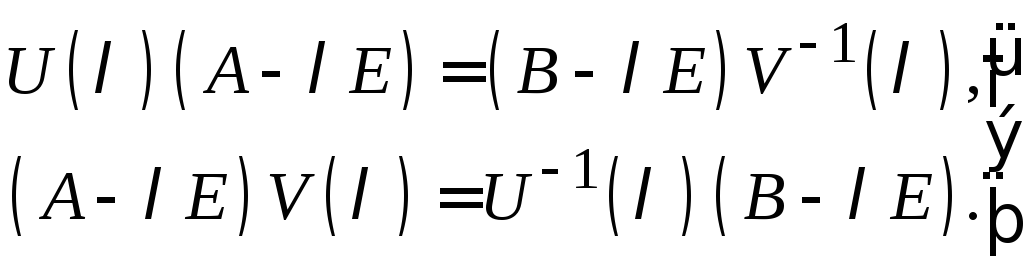(2)

Так как матрицаимеет постепень, причем старшим коэффициентом соответствующего матричного многочлена служит невырожденная матрица, то к матрицамиможно применить алгоритм деления с остатком. Значит, существуют такие матрицыи, причём, степень, если, равнапо, что

. (3)

Аналогично

. (4)

Используя (3) и (4) и учитывая (1), получаем:

или, применяя (2),

Квадратная скобка, стоящая справа, равна в действительности нулю: в противном случае она, являясь матрицей, так как ииестьматрицы, имела бы по меньшей мере степень, а тогда степень фигурной скобки была бы не меньшеи, следовательно, степень всей правой части была бы не меньше. Это, однако, невозможно, так как слева стоитматрица степени.

Таким образом,

,

откуда, приравнивая матричные коэффициенты при одинаковых степенях , получаем

, (5)

. (6)

Равенство (6) показывает, что числовая матрица не только отлична от нуля, но даже является невырожденной, причем

,

а тогда равенство (5) принимает вид

,

что и доказывает подобие матриц и. □

Пример 3. Являются ли следующие матрицы подобными

, ?

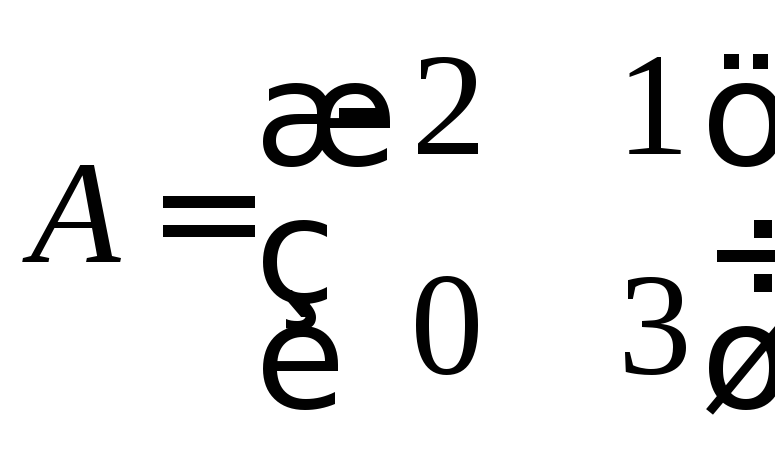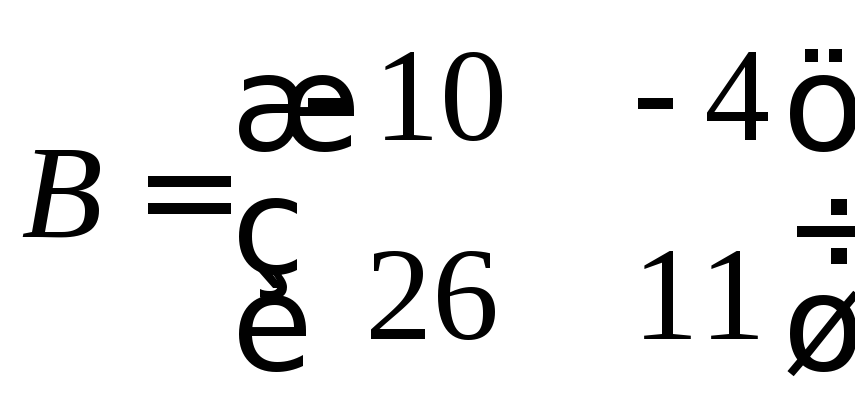Решение. Их характеристические матрицы эквивалентны, так как приводятся к одному и тому же каноническому виду

,

поэтому матрицы иподобны.