
- •Глава I. Линейные операторы в евклидовом и унитарном пространствах.
- •§1.1. Евклидовы и унитарные пространства.
- •§1.2. Изоморфизм унитарных пространств.
- •§1.3. Линейные функции.
- •§1.4. Сопряжённые операторы.
- •§1.5. Нормальные операторы.
- •§1.6. Унитарные операторы.
- •§1.7. Эрмитовы (самосопряжённые) операторы.
- •§1.8. Кососимметрические операторы.
- •§1.9. Неотрицательные линейные операторы.
- •§1.10. Линейные операторы в евклидовом пространстве.
- •Глава II. Квадратичные формы.
- •§2.1. Приведение квадратичной формы к каноническому виду.
- •§2.2. Приведение квадратичной формы к главным осям.
- •§2.3. Закон инерции.
- •§2.4. Распадающиеся квадратичные формы.
- •§2.5. Положительно определенные формы.
- •§2.6. Пары форм.
- •Глава III. Жорданова нормальная форма матрицы.
- •§3.1. Матрицы, их эквивалентность.
- •§3.2. Унимодулярные -матрицы.
- •§3.3. Матричные многочлены.
- •§3.4. Связь подобия числовых матриц с
- •§ 3.5. Жорданова нормальная форма.
- •§ 3.6. Приведение матрицы к жордановой нормальной форме.
- •§ 3.7. Минимальный многочлен.
- •Глава I. Линейные операторы в евклидовом
§ 3.7. Минимальный многочлен.
Пусть дана
квадратная матрица
![]() порядка
порядка![]() с элементами из поля
с элементами из поля![]() .
Если
.
Если
![]()
произвольный
многочлен из кольца
![]() ,
то матрица
,
то матрица
![]()
будет называться
значением
многочлена
![]() при
при![]() .
.
Нетрудно проверить,
что если
![]() или
или
![]() ,
то
,
то
![]() и, соответственно,
и, соответственно,![]() .
.
Если многочлен
![]() аннулируется матрицей
аннулируется матрицей
![]() ,
т. е.
,
т. е.![]() ,
то матрицу
,
то матрицу![]() будем называтьматричным
корнем многочлена
будем называтьматричным
корнем многочлена
![]() .
.
УТВЕРЖДЕНИЕ 1.
Всякая
матрица
![]() служит корнем некоторого ненулевого
многочлена.
служит корнем некоторого ненулевого
многочлена.
ДОКАЗАТЕЛЬСТВО.
Известно, что все квадратные матрицы
порядка
![]() составляют над полем
составляют над полем![]()
![]() мерное
векторное пространство. Отсюда следует,
что система из
мерное
векторное пространство. Отсюда следует,
что система из![]() матриц
матриц
![]()
линейно зависима
над полем
![]() ,
т. е. в
,
т. е. в![]() существуют такие элементы
существуют такие элементы
![]() ,
не все равные нулю, что
,
не все равные нулю, что
![]() .
.
Таким образом,
матрица
![]() оказалась корнем ненулевого многочлена
оказалась корнем ненулевого многочлена
![]() ,
,
степень которого
не превосходит
![]() .
□
.
□
Матрица
![]() является корнем и для некоторых таких
многочленов, старшие коэффициенты
которых равны единице
является корнем и для некоторых таких
многочленов, старшие коэффициенты
которых равны единице
![]() достаточно взять любой ненулевой
многочлен, аннулируемый матрицей
достаточно взять любой ненулевой
многочлен, аннулируемый матрицей
![]() ,
и разделить этот многочлен на его
старший коэффициент. Многочлен наименьшей
степени со старшим коэффициентом
,
и разделить этот многочлен на его
старший коэффициент. Многочлен наименьшей
степени со старшим коэффициентом
![]() ,
аннулируемый, матрицей
,
аннулируемый, матрицей
![]() ,
называется минимальным
многочленом матрицы
,
называется минимальным
многочленом матрицы
![]() .
Заметим, что минимальный многочлен
матрицы
.
Заметим, что минимальный многочлен
матрицы
![]() определен однозначно, так как разность
двух таких многочленов имела бы меньшую
степень, чем каждый из них, но также
аннулировалась бы матрицей
определен однозначно, так как разность
двух таких многочленов имела бы меньшую
степень, чем каждый из них, но также
аннулировалась бы матрицей
![]() .
.
УТВЕРЖДЕНИЕ 2.
Всякий
многочлен
![]() ,
аннулируемый матрицей
,
аннулируемый матрицей![]() ,
делится нацело на минимальный многочлен
,
делится нацело на минимальный многочлен![]() этой матрицы.
этой матрицы.
ДОКАЗАТЕЛЬСТВО.
Разделим
![]() на
на
![]() с остатком
с остатком
![]() ,
,
тогда
![]()
и из того, что
![]() следует
следует![]() ,
но степень
,
но степень![]() меньше степени
меньше степени![]() ,
что противоречит определению минимального
многочлена. □
,
что противоречит определению минимального
многочлена. □
Для доказательства основной теоремы данного параграфа потребуется вспомогательное утверждение.
ЛЕММА. Пусть
![]() ,
,
![]() .
(1)
.
(1)
Если
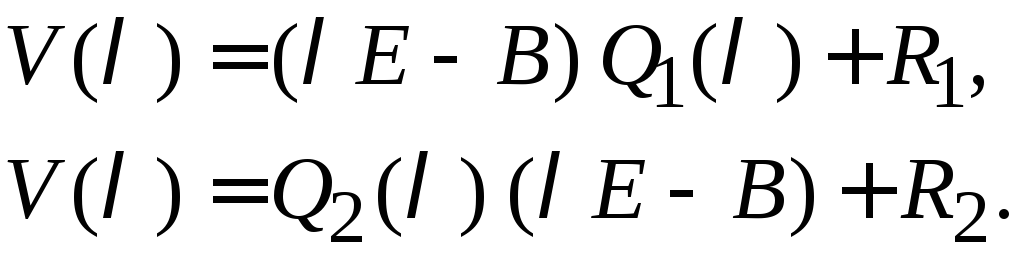 (2)
(2)
то
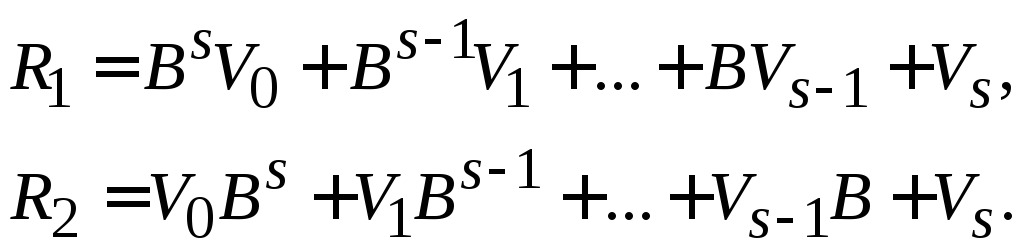 (3)
(3)
ДОКАЗАТЕЛЬСТВО.
Достаточно доказать хотя бы первое из
двух утверждений леммы
![]() второе доказывается аналогично.
Доказательство состоит в непосредственной
проверке справедливости равенства
(2), если многочлен
второе доказывается аналогично.
Доказательство состоит в непосредственной
проверке справедливости равенства
(2), если многочлен![]() будет заменен его записью (1), вместо
будет заменен его записью (1), вместо
![]() будет подставлено (3), а в качестве
будет подставлено (3), а в качестве
![]() будет взят многочлен
будет взят многочлен
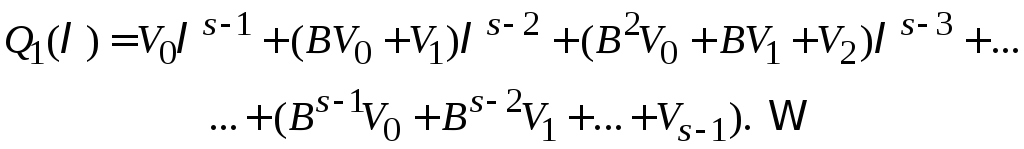
ТЕОРЕМА 1. Минимальный
многочлен матрицы
![]() совпадает с последним инвариантным
множителем
совпадает с последним инвариантным
множителем![]() характеристической матрицы
характеристической матрицы![]() .
.
ДОКАЗАТЕЛЬСТВО. Как следует из § 3.1
![]() .
(4)
.
(4)
Значит, многочлены
![]() и
и![]() не будут нулевыми. Обозначим, далее,
через
не будут нулевыми. Обозначим, далее,
через![]() матрицу, составленную из алгебраических
дополнений матрицы
матрицу, составленную из алгебраических
дополнений матрицы![]() ,
причём алгебраические дополнения
элементов каждой строки располагаются
в соответствующем столбце.
,
причём алгебраические дополнения
элементов каждой строки располагаются
в соответствующем столбце.
![]()
Тогда справедливо равенство
![]() .
(5)
.
(5)
С другой стороны,
так как элементами матрицы
![]() служат взятые со знаками плюс или минус
миноры
служат взятые со знаками плюс или минус
миноры![]() го
порядка матрицы
го
порядка матрицы![]() и только они, а многочлен
и только они, а многочлен![]() есть общий наибольший делитель всех
этих миноров, то
есть общий наибольший делитель всех
этих миноров, то
![]() ,
(6)
,
(6)
причем наибольший
общий делитель элементов матрицы
![]() равен
равен
![]() .
.
Из равенств (5), (6) и (4) вытекает равенство
![]() .
.
Это равенство
можно сократить на ненулевой множитель
![]() .
Таким образом,
.
Таким образом,
![]() ,
,
откуда
![]() .
(7)
.
(7)
Это равенство
показывает, что остаток от деления
![]() матрицы
матрицы![]() слева, на двучлен
слева, на двучлен![]() равен нулю. Из леммы вытекает, что этот
остаток равен матрице
равен нулю. Из леммы вытекает, что этот
остаток равен матрице![]() .
Действительно, матрица
.
Действительно, матрица![]() может быть записана как матричный
может быть записана как матричный![]() многочлен,
коэффициенты которого являются
скалярными матрицами, т. е. перестановочные
с матрицей
многочлен,
коэффициенты которого являются
скалярными матрицами, т. е. перестановочные
с матрицей![]() .
Таким образом
.
Таким образом
![]() ,
т. е. многочлен
,
т. е. многочлен
![]() действительно аннулируется матрицей
действительно аннулируется матрицей![]() .
.
Отсюда следует,
что многочлен
![]() нацело делится на минимальный
нацело делится на минимальный![]() многочлен матрицы
многочлен матрицы![]() ,
,
![]() .
(8)
.
(8)
Ясно, что старший
коэффициент многочлена
![]() равен единице.
равен единице.
Так как
![]() ,
то по лемме остаток от левого деления
,
то по лемме остаток от левого деления![]() матрицы
матрицы![]() на двучлен
на двучлен![]() равен нулю, т. е.
равен нулю, т. е.
![]() .
(9)
.
(9)
Равенства (8), (7) и (9) приводят к равенству
![]() .
.
Обе части этого
равенства можно сократить на общий
множитель
![]() ,
так как старший коэффициент
,
так как старший коэффициент![]() этого матричного
этого матричного![]() многочлена
является невырожденной матрицей. Таким
образом,
многочлена
является невырожденной матрицей. Таким
образом,
![]() .
.
Мы помним, однако,
что наибольший общий делитель элементов
матрицы
![]() равен
равен
![]() .
Поэтому многочлен
.
Поэтому многочлен![]() должен иметь нулевую степень, а так как
его старший коэффициент равен
должен иметь нулевую степень, а так как
его старший коэффициент равен![]() ,
то
,
то![]() .
Таким образом, ввиду (8),
.
Таким образом, ввиду (8),![]()
![]() что и требовалось доказать. □
что и требовалось доказать. □
Так как, ввиду
(4), характеристический многочлен матрицы
![]() нацело делится на многочлен
нацело делится на многочлен![]() ,
то из доказанной сейчас теоремы вытекает
следующая
,
то из доказанной сейчас теоремы вытекает
следующая
ТЕОРЕМА 2 (Гамильтона
![]() Кэли).Всякая
матрица является корнем своего
характеристического многочлена.
□
Кэли).Всякая
матрица является корнем своего
характеристического многочлена.
□
ТЕОРЕМА 3. Если
матрицы
![]() и
и![]() подобны и если многочлен
подобны и если многочлен![]() аннулируется матрицей
аннулируется матрицей![]() ,
то он аннулируется и матрицей
,
то он аннулируется и матрицей![]() .
.
ДОКАЗАТЕЛЬСТВО.
Действительно, пусть
![]() .
.
Если
![]() ,
то
,
то
![]() .
.
Трансформируя
обе части этого равенства матрицей
![]() ,
получаем:
,
получаем:
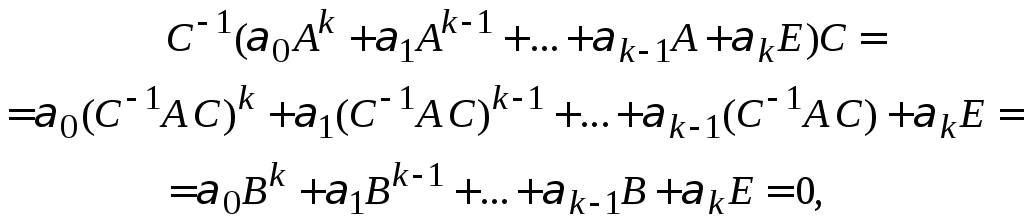
т.е.
![]() .
□
.
□
СЛЕДСТВИЕ. Подобные матрицы обладают одним и тем же минимальным многочленом. □
Пусть теперь
![]() линейный оператор в
линейный оператор в![]() мерном
линейном пространстве над полем
мерном
линейном пространстве над полем![]() .
Матрицы, задающие этот оператор в разных
базисах пространства, подобны между
собой. Общий минимальный многочлен
этих матриц называетсяминимальным
многочленом линейного оператора
.
Матрицы, задающие этот оператор в разных
базисах пространства, подобны между
собой. Общий минимальный многочлен
этих матриц называетсяминимальным
многочленом линейного оператора
![]() .
.
Используя операции над линейными операторами [2] можно ввести понятие значения многочлена
![]()
из кольца
![]() при
при![]() ,
равном линейному оператору
,
равном линейному оператору![]() :
это
:
это
будет линейный оператор
![]() ,
,
где
![]() тождественный оператор.
тождественный оператор.
Будем говорить,
что многочлен
![]() аннулируется
линейным оператором
аннулируется
линейным оператором
![]() ,
если
,
если
![]() ,
где
,
где
![]() нулевой оператор.
нулевой оператор.
Учитывая связь между операциями над линейными операторами и над матрицами можно доказать следующее утверждение.
ТЕОРЕМА 4. Минимальный
многочлен линейного оператора
![]() является тем однозначно определенным
многочленом наименьшей степени со
старшим коэффициентом
является тем однозначно определенным
многочленом наименьшей степени со
старшим коэффициентом![]() ,
который аннулируется оператором
,
который аннулируется оператором![]() .
□
.
□
После этого
результаты, полученные выше, в частности
теорема Гамильтона
![]() Кэли, могут быть переформулированы на
языке линейных операторов.
Кэли, могут быть переформулированы на
языке линейных операторов.
ЗАДАЧИ К ГЛАВЕ III.
22. Привести
следующие
![]() матрицы
к нормальной диагональной форме
посредством элементарных преобразований:
матрицы
к нормальной диагональной форме
посредством элементарных преобразований:
а)
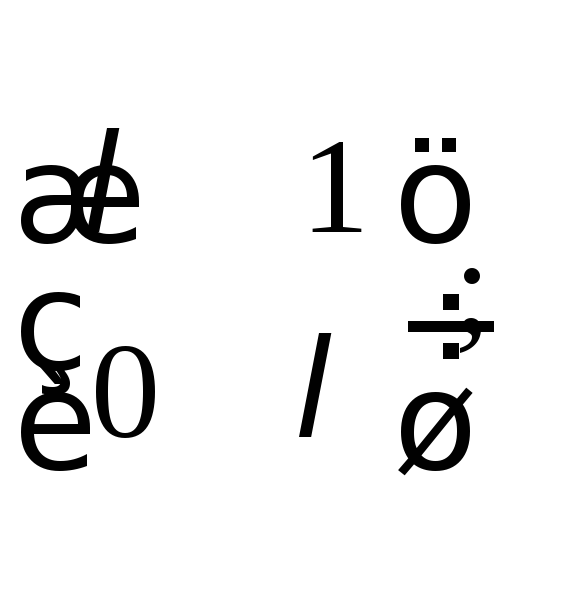
б)

в)
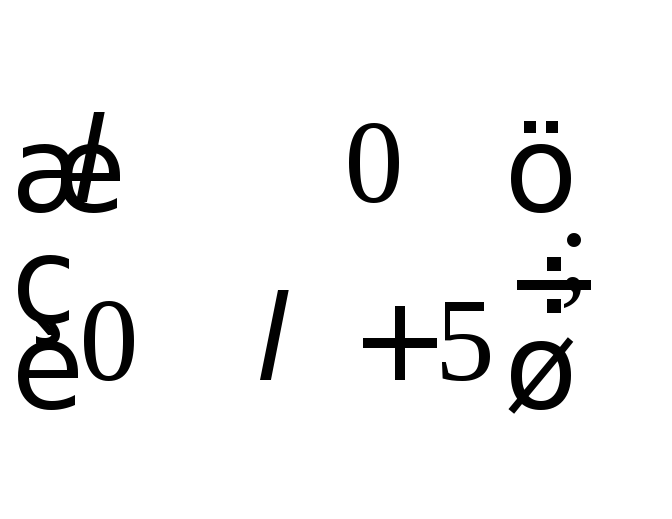
г)
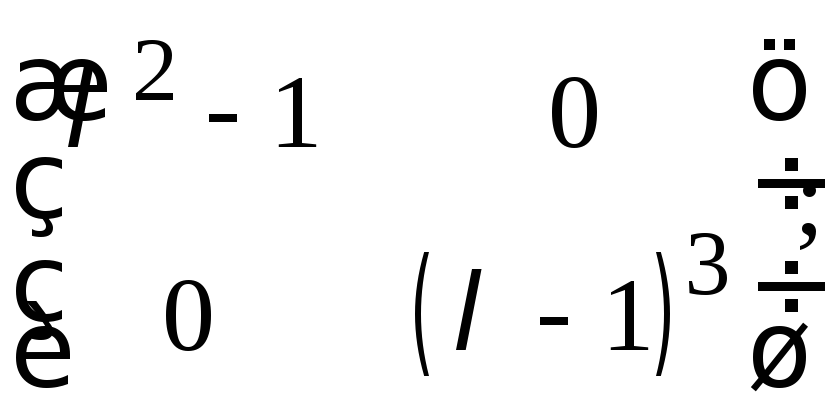
д)
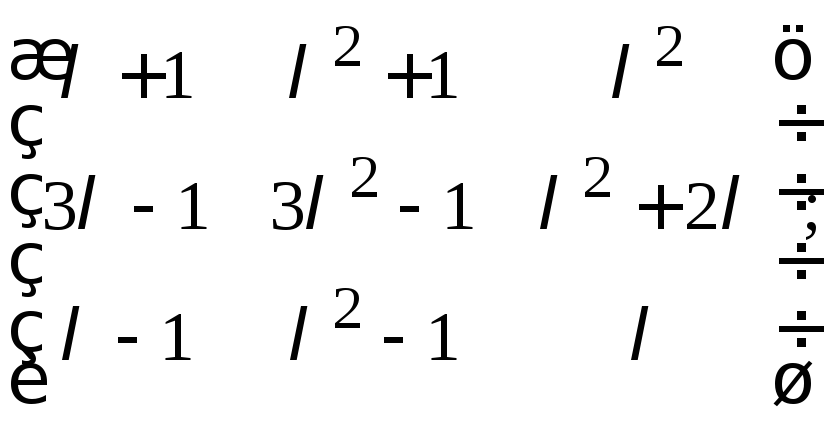
е)

ж)

з)
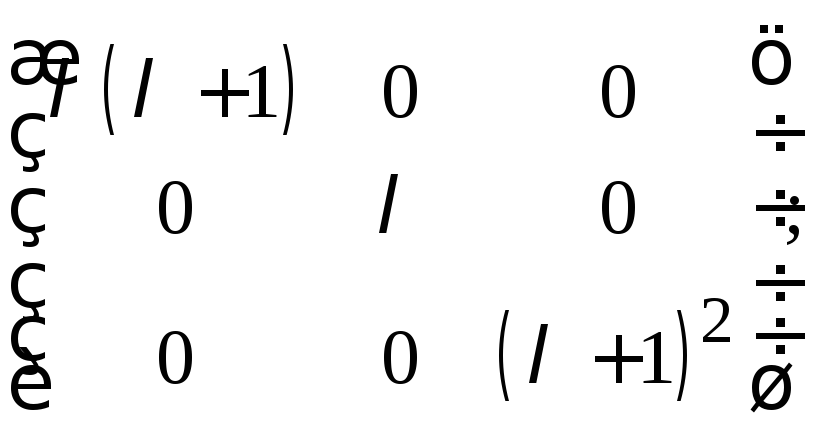
и)

23. Привести
следующие
![]() матрицы
к нормальной диагональной форме методом
нахождения делителей миноров:
матрицы
к нормальной диагональной форме методом
нахождения делителей миноров:
а)
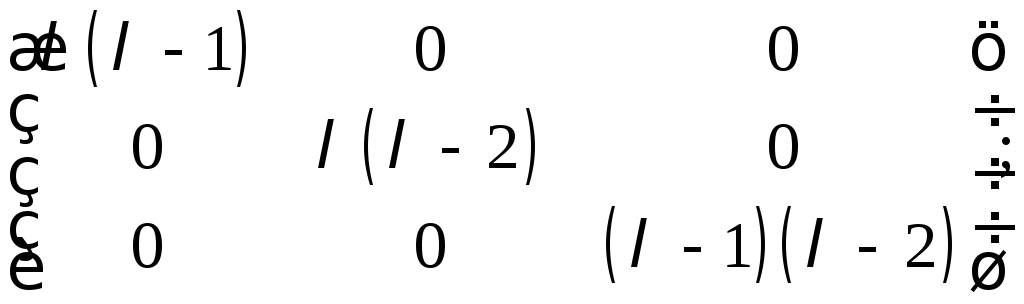
б)

в)

24. Привести
следующие
![]() матрицы
к нормальной диагональной форме
используя комбинированный метод:
матрицы
к нормальной диагональной форме
используя комбинированный метод:
а)

б)

в)

г)
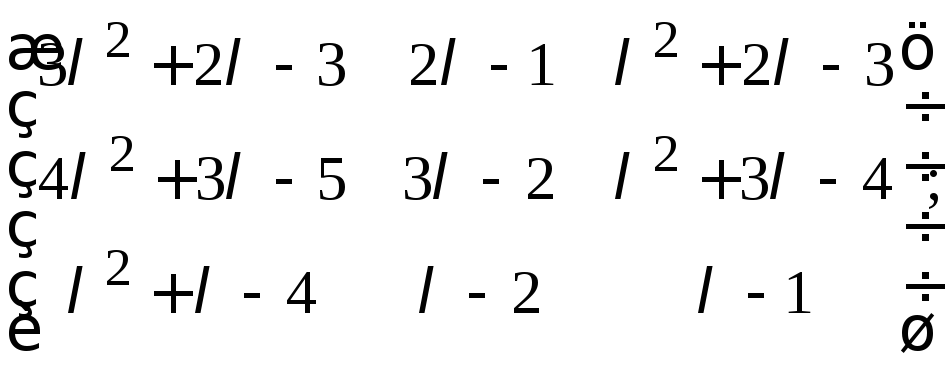
д)
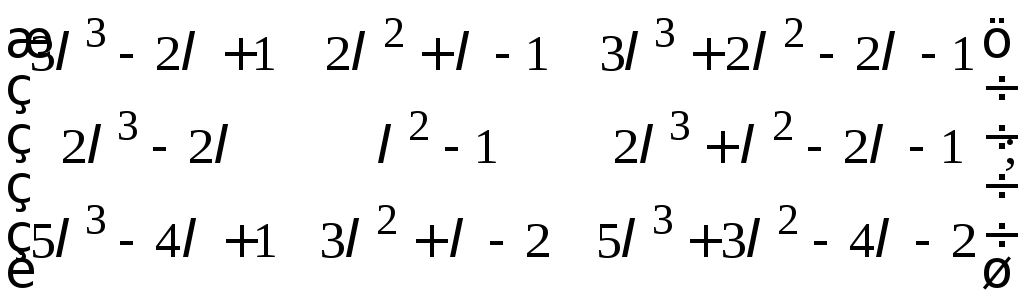
е)

25. Выяснить,
эквивалентны ли между собой следующие
![]() матрицы:
матрицы:
а)
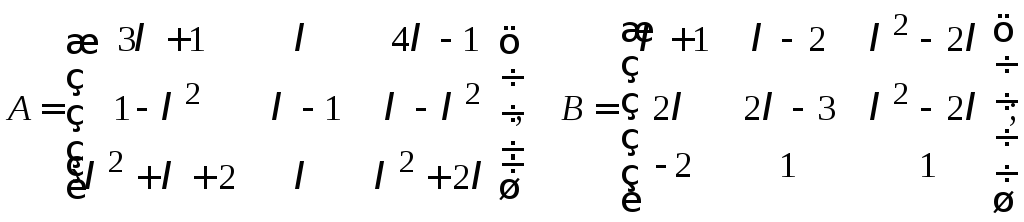
б)
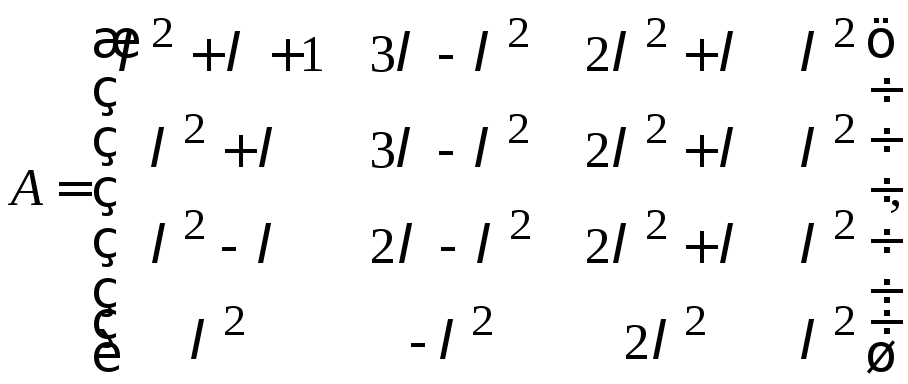
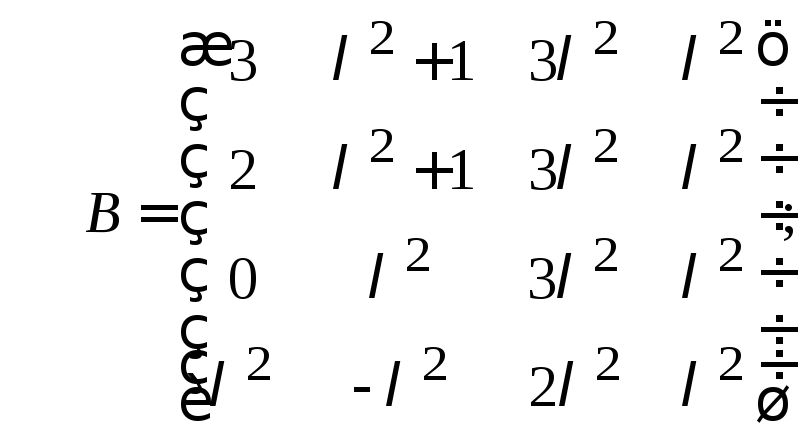
в)
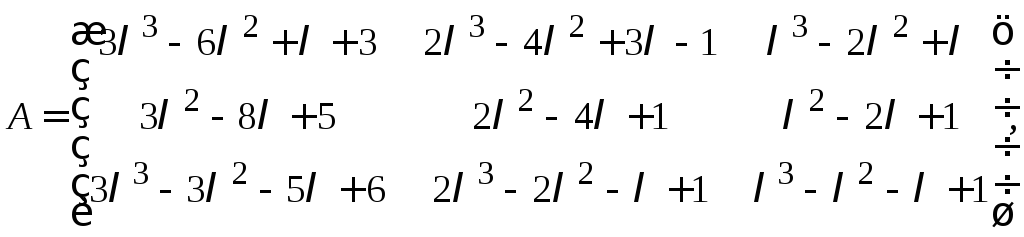
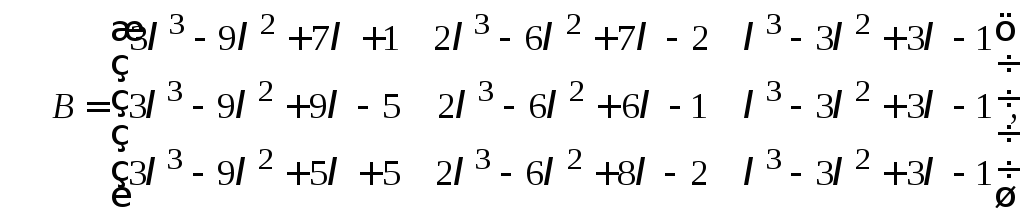
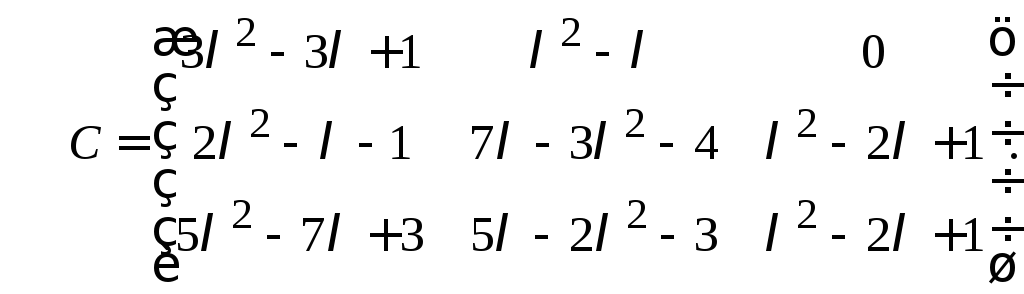
26. Найти элементарные делители следующих матриц:
а)
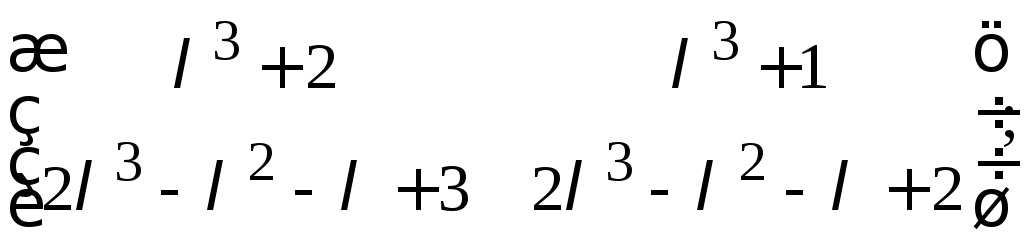
б)

в)

27. Найти нормальную
диагональную форму квадратной
![]() матрицы,
если известны её элементарные делители,
ранг
матрицы,
если известны её элементарные делители,
ранг![]() и порядок
и порядок![]() :
:
а)
![]()
б)
![]()
в)
![]()
28. Выяснить, являются ли подобными между собой следующие матрицы:
а)
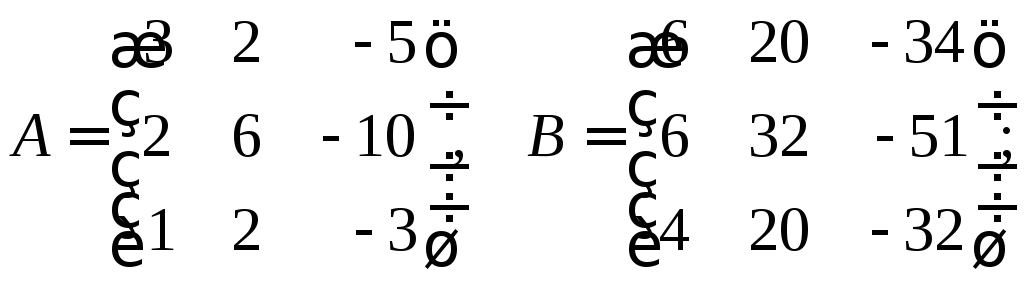
б)
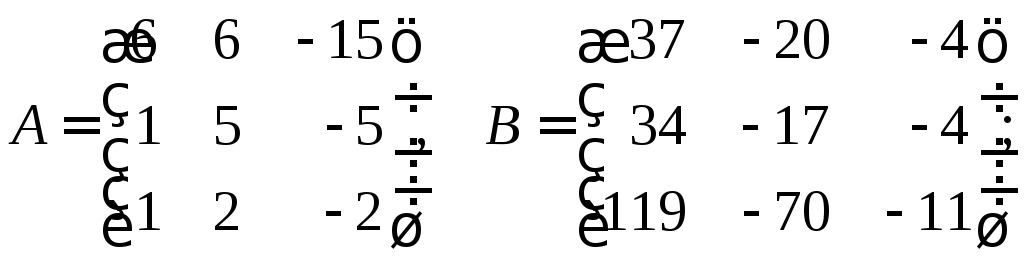
в)
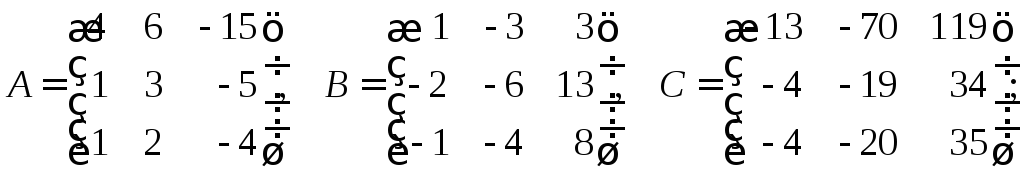
г)
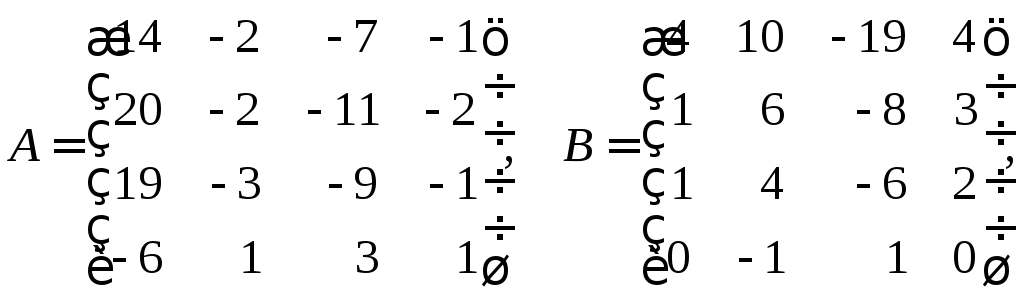
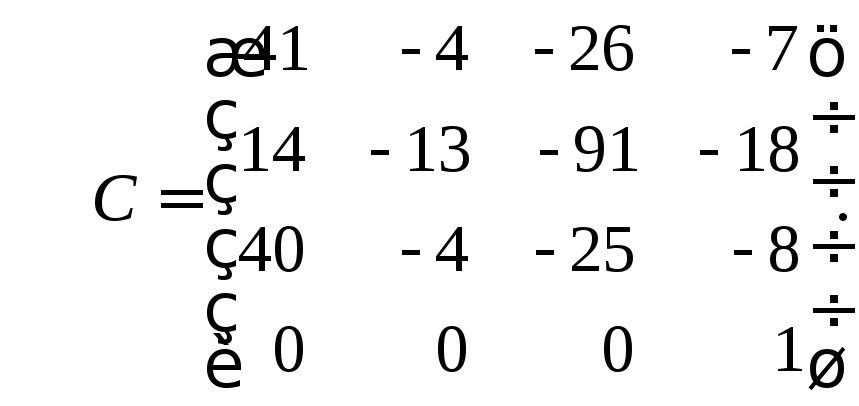
29.
а)

б)

в)
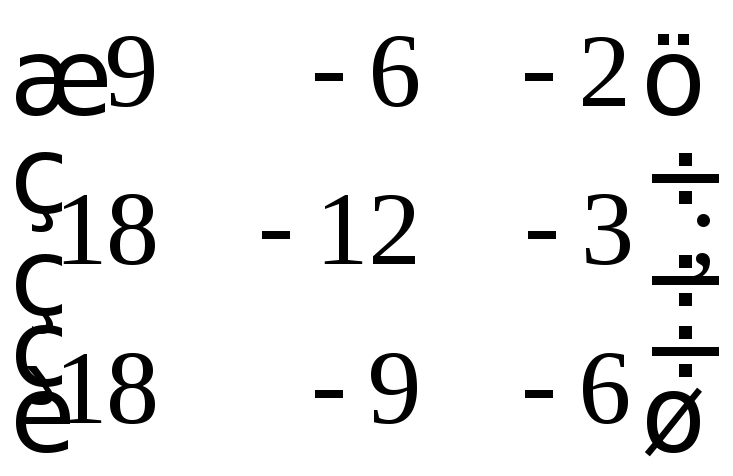
г)

д)
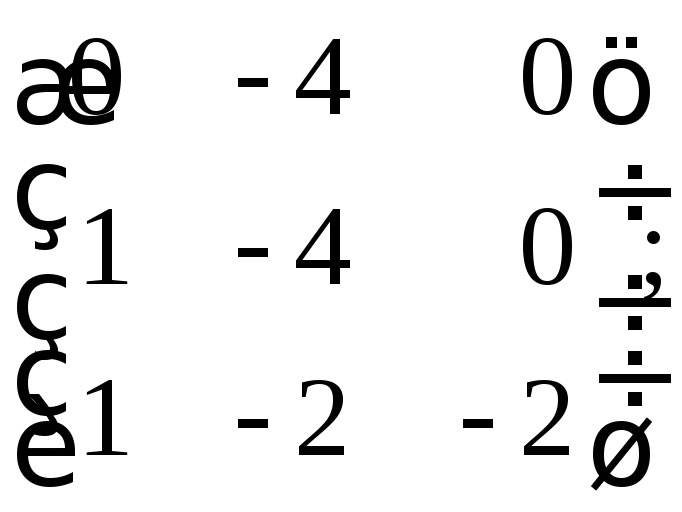
е)

ж)
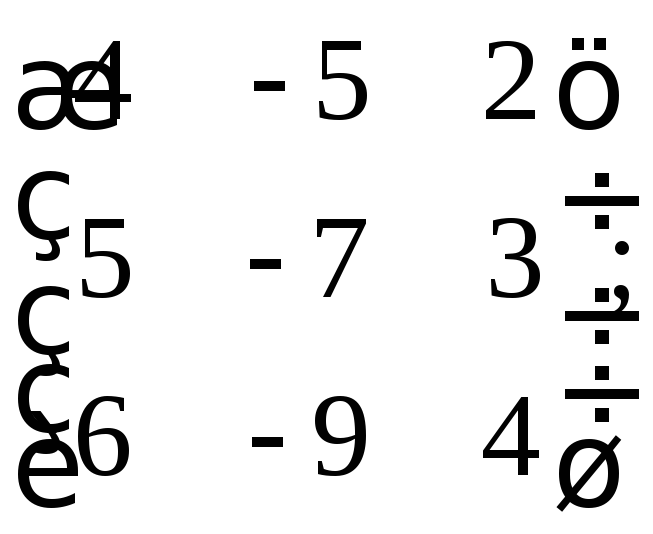
з)

и)
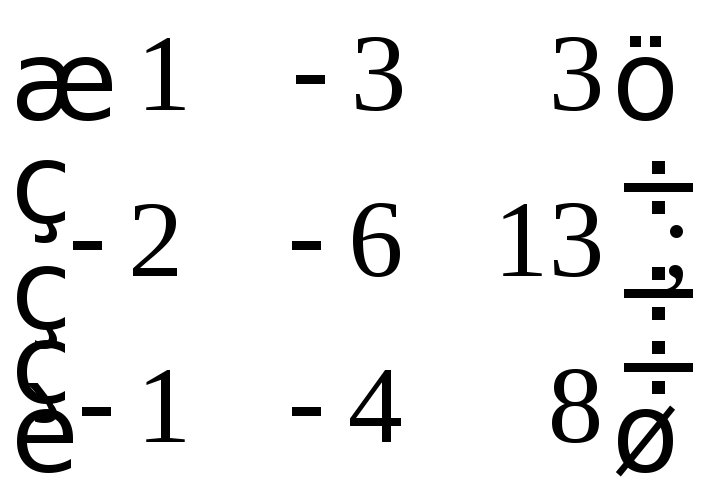
к)
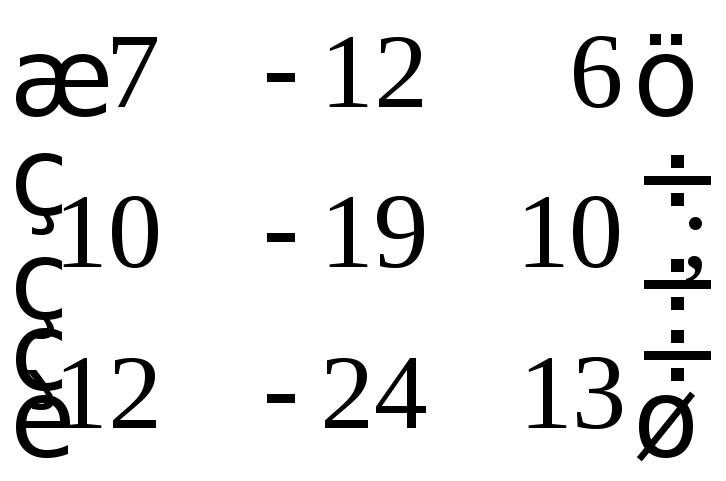
л)

м)

н)

о)

п)

30. Выяснить, являются ли следующие матрицы подобными некоторым диагональным матрицам в полях рациональных, вещественных и комплексных чисел:
а)

б)

в)
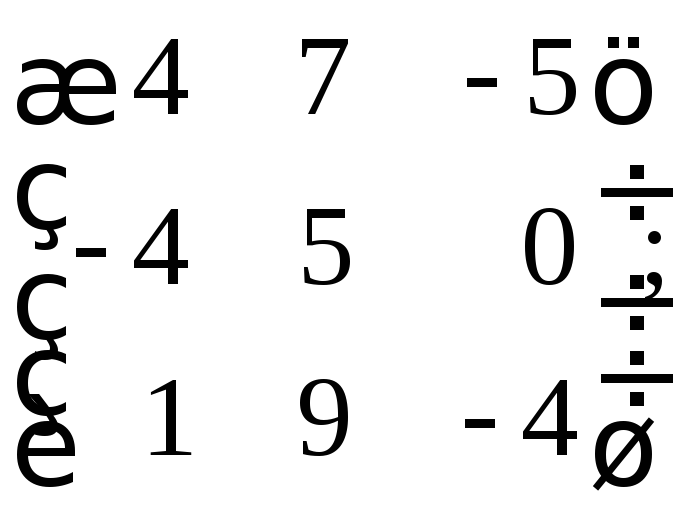
г)
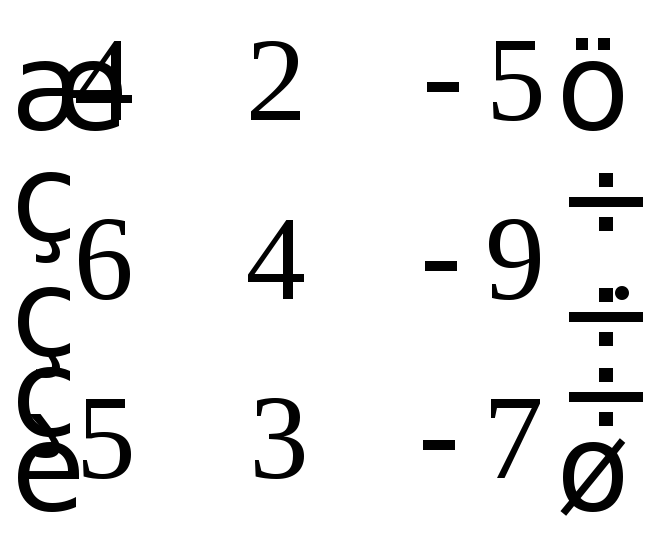
31. Найти минимальные многочлены следующих матриц:
а)

б)
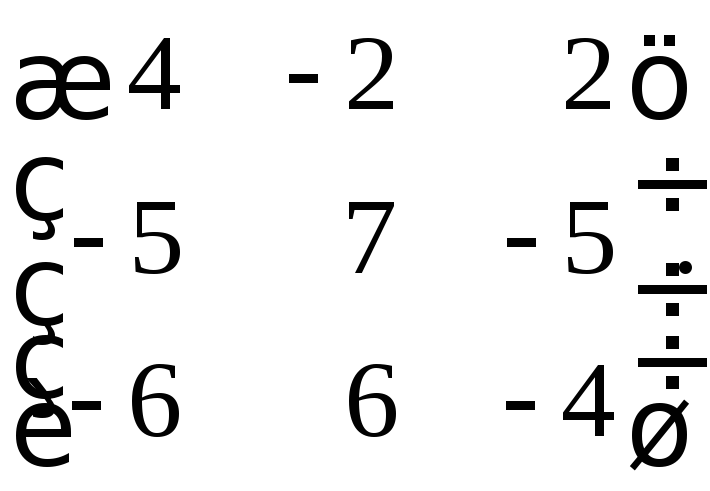
ОТВЕТЫ.
1.
а) да;
б) нет;
в) да;
г) да;
д) нет.
2.
а) да;
б) нет;
в) да;
г) да;
д) нет;
е) нет;
ж) да.
3.
а) нет;
б) да;
в) да;
г) нет;
д) да;
е) нет;
ж) да.
4.
а)
 ;
;
б)
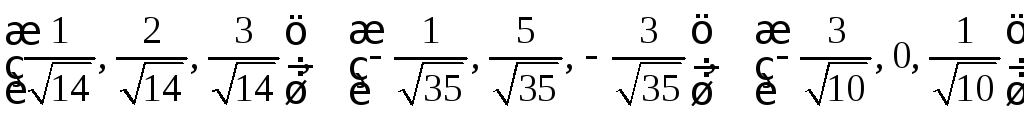 ;
;
в)
 .
.
5.
а)
 ;
;
б)
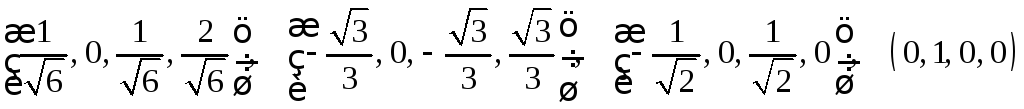 .
.
6.
а)
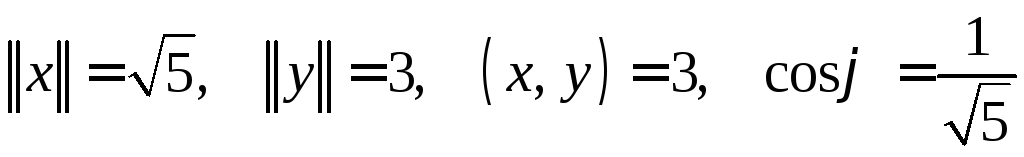 ;
;
б)
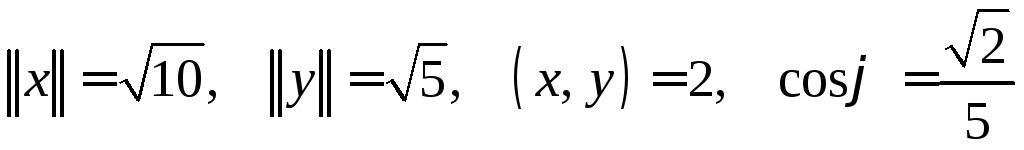 ;
;
в)
![]() .
.
7.
а) нет;
б)
да,
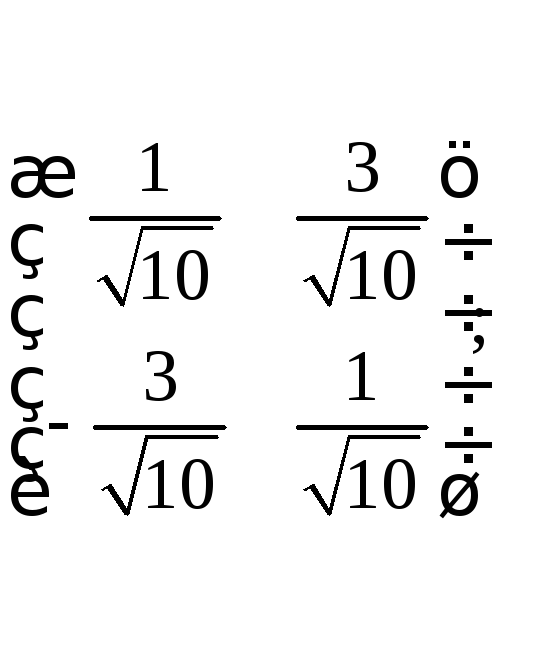
в)
да,

г) нет;
д)
да,

е)
да,
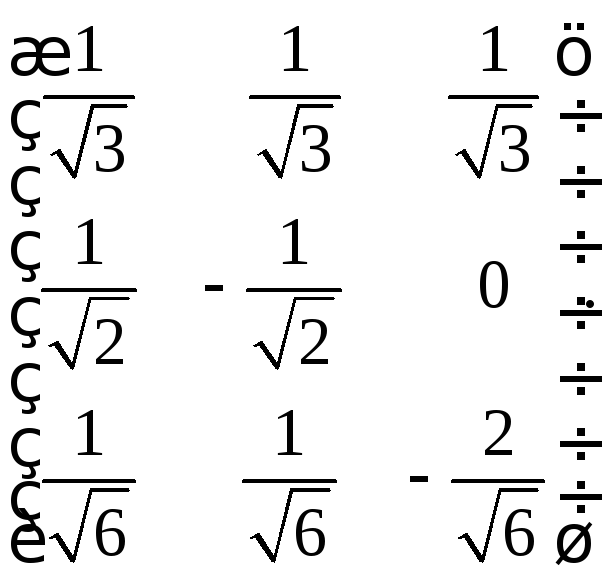
8.
![]() .
.
9.
а) нет;
б) да;
в) да.
10.
Диагональная матрица является
ортогональной тогда и только тогда,
когда каждый диагональный элемент
равен
![]() .
.
11.
а)

б)

в)
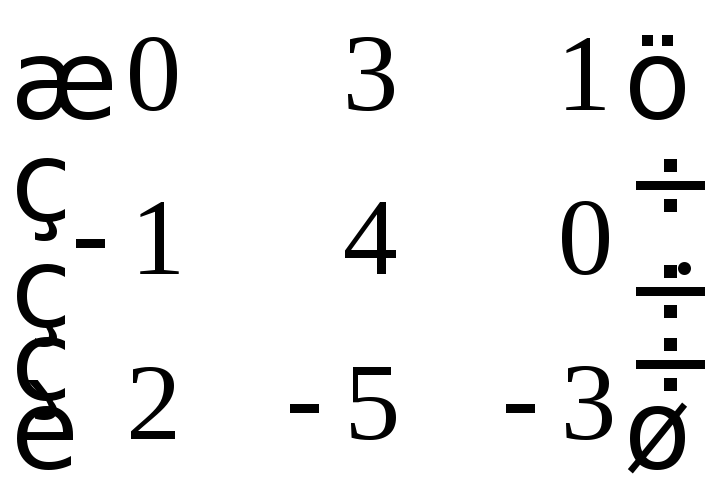
12.
а) нет;
б) да;
в) нет;
г) да.
13.
а)
![]()
б)
ни при каком
![]()
14.
а)

б)
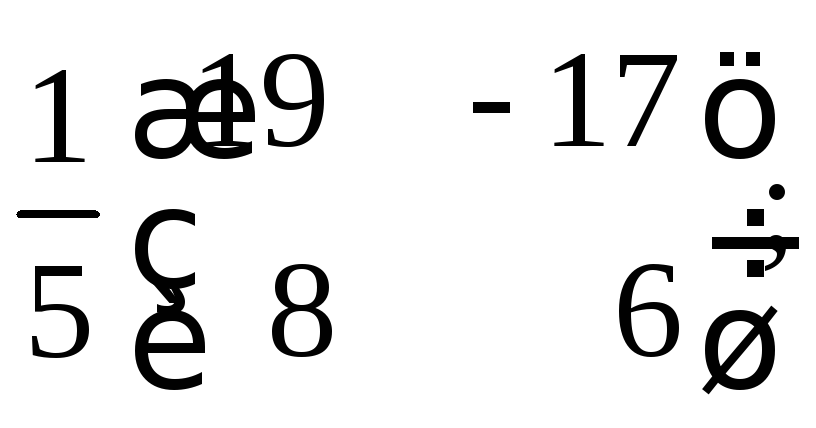
в)
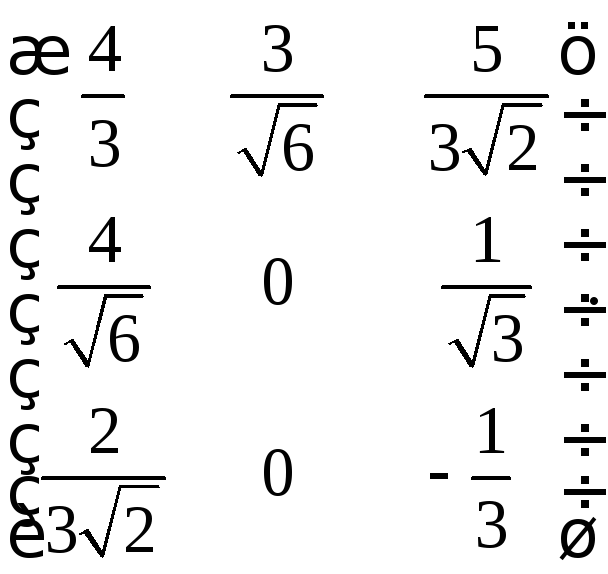
15.
а)

б)
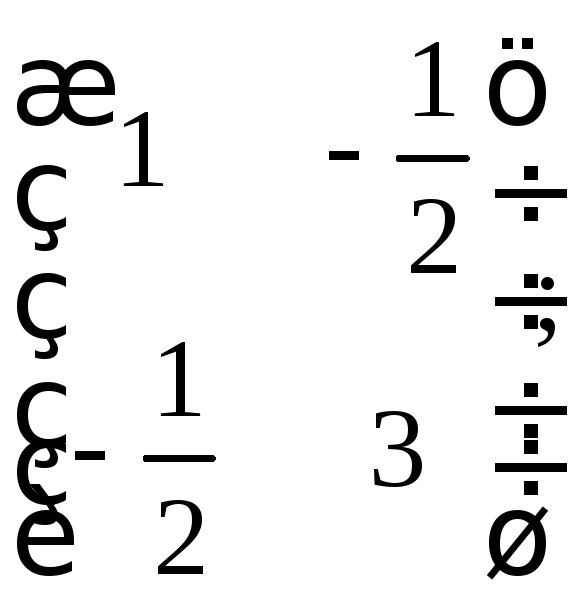
в)
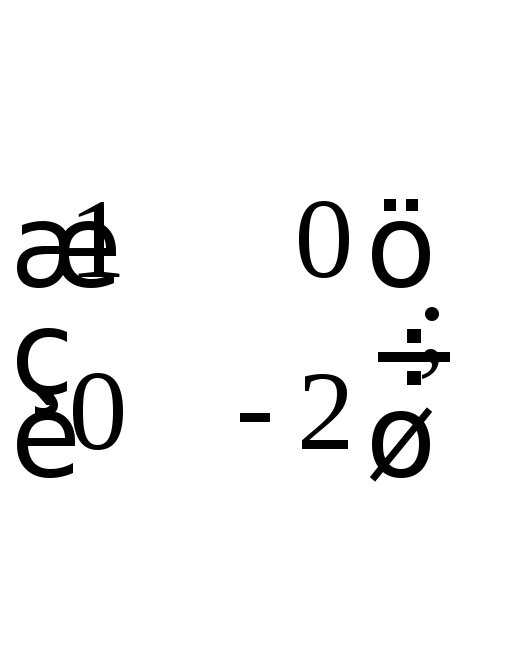
г)

д)

е)

ж)
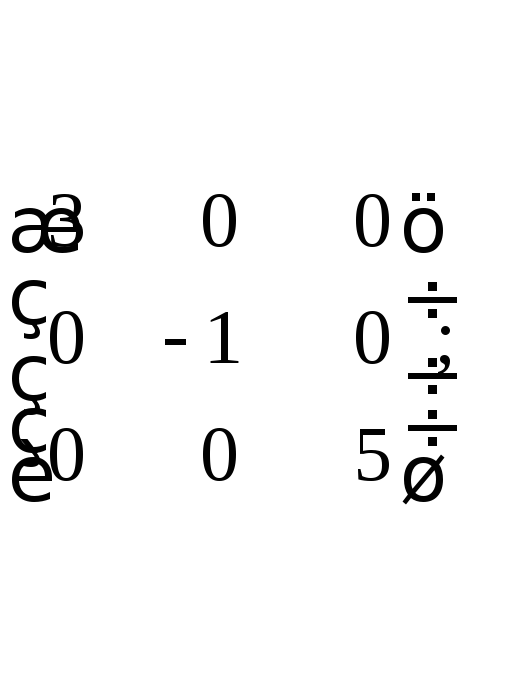
з)

и)

к)

16.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() .
.
17.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
18. Ответ определяется неоднозначно.
а)
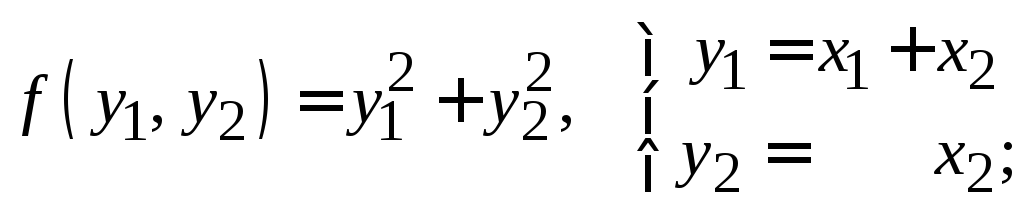
б)
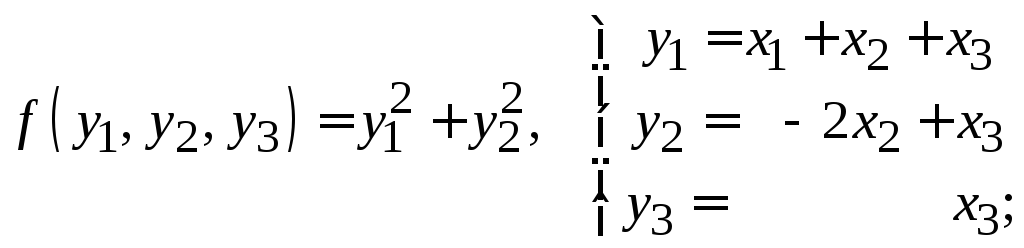
в)
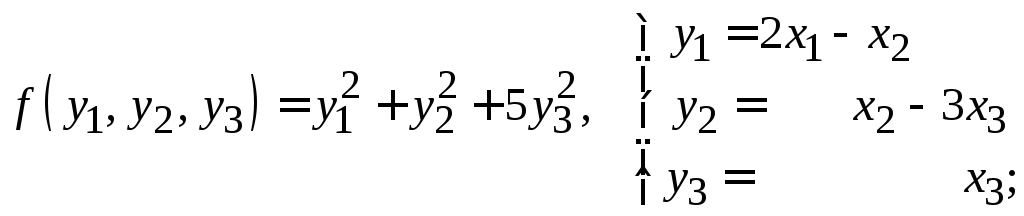
г)

д)
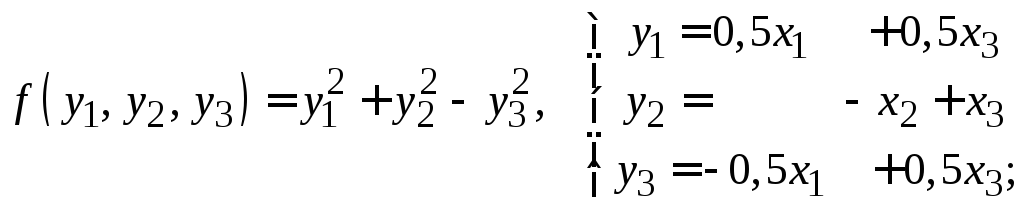
е)
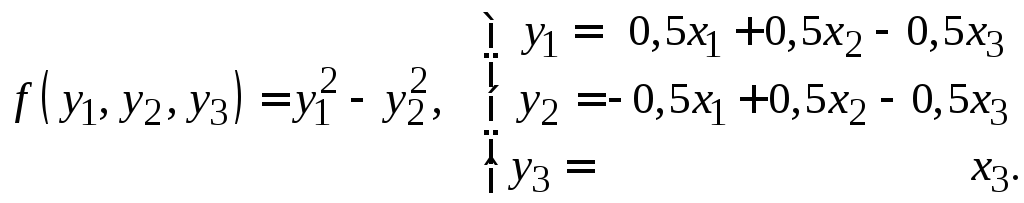
19. Ответ определяется неоднозначно.
а)
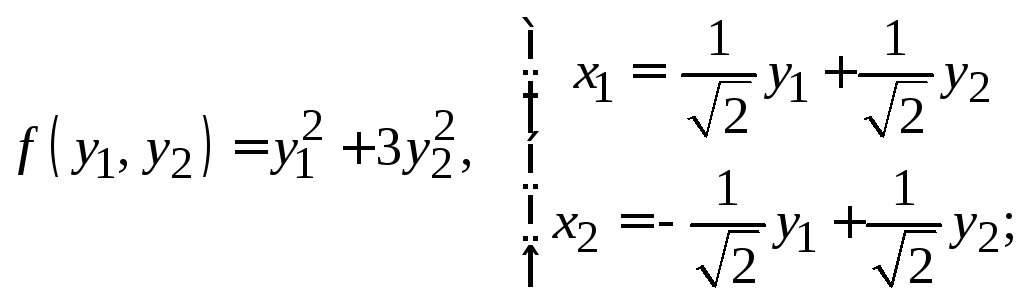
б)

в)

г)

д)
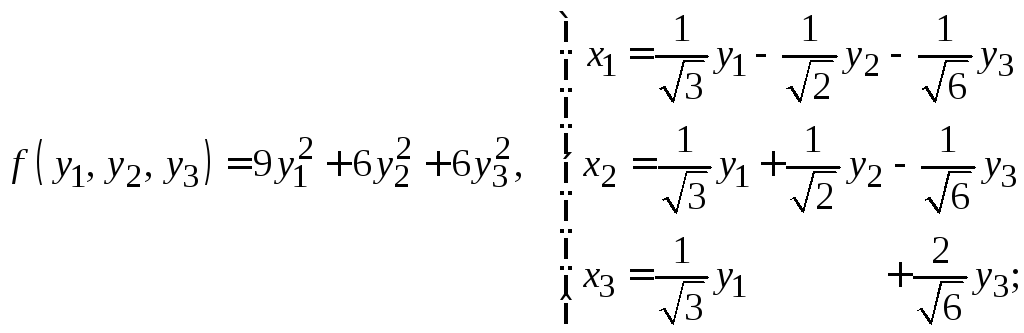
е)

ж)
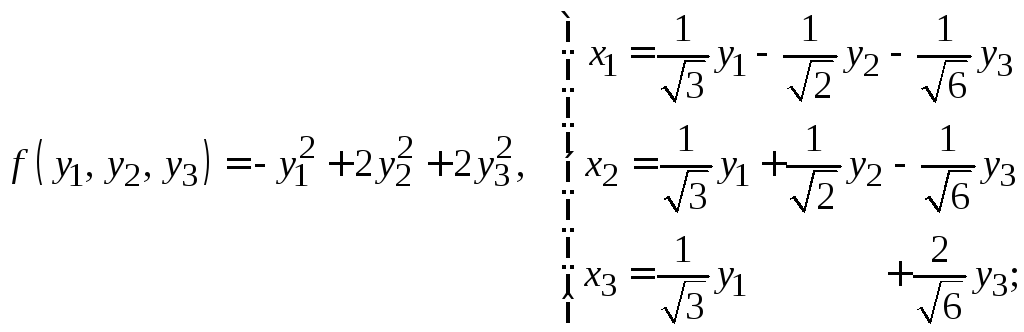
з)
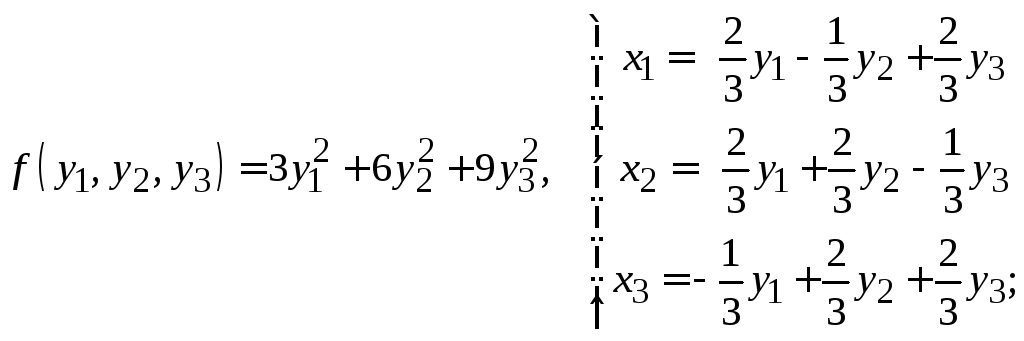
и)
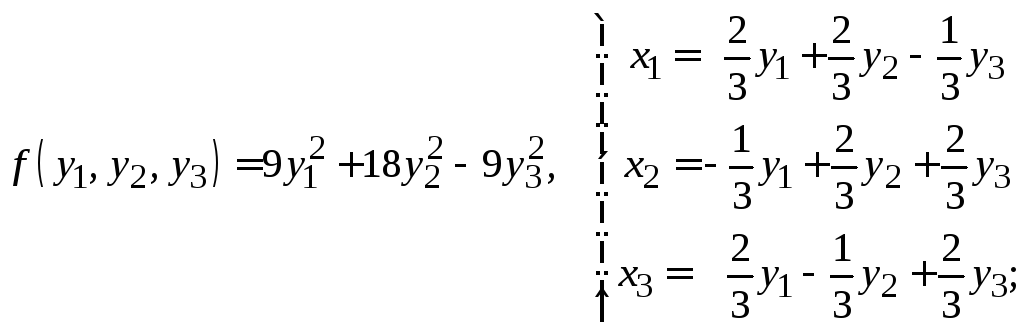
к)
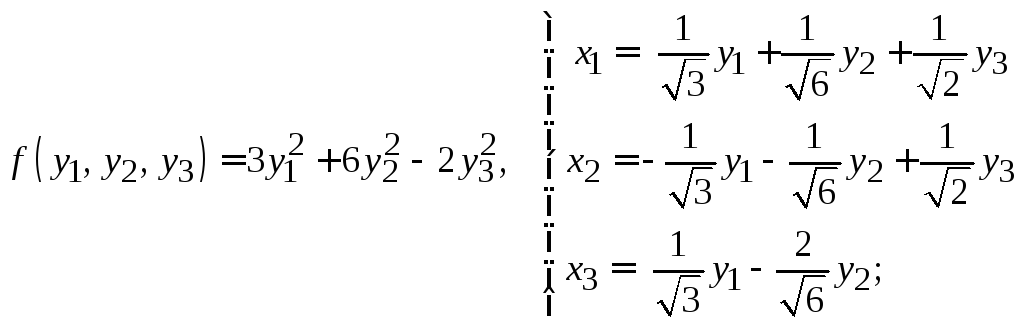
л)

м)
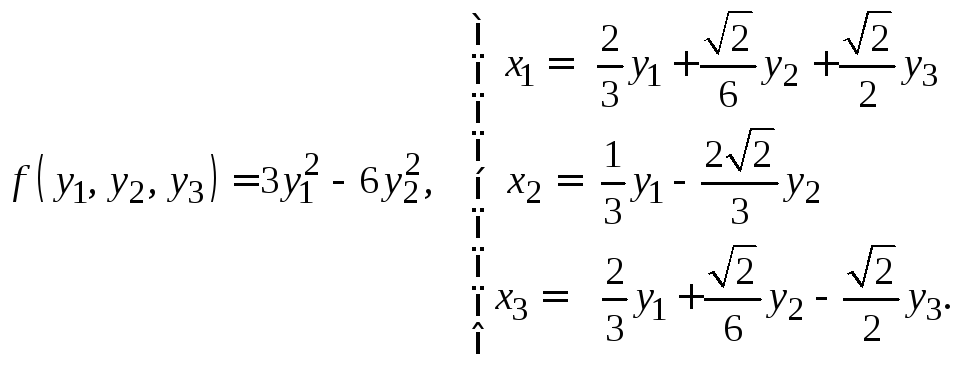
20.
а) положительно определённая;
б) не является знакоопределённой;
в) не является знакоопределённой;
г) положительно определённая;
д) отрицательно определённая;
е) не является знакоопределённой.
21.
а)
для любого
![]() ;
;
б)
ни при каком значении
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
ни при каком значении
![]() ;
;
е)
![]() ;
;
ж)
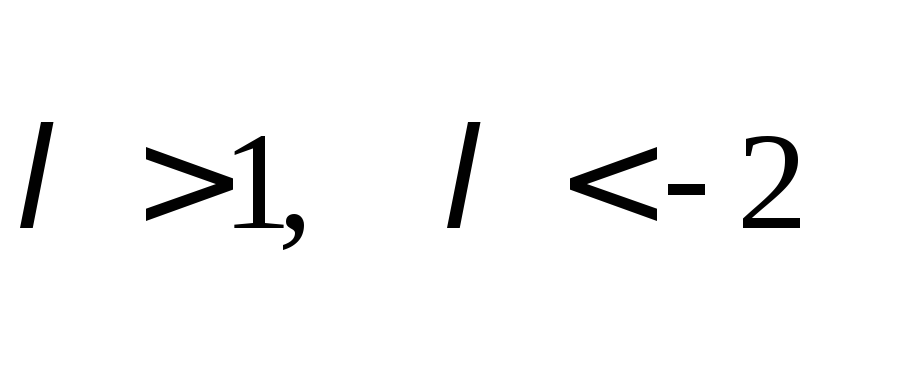 .
.
22.
а)

б)

в)
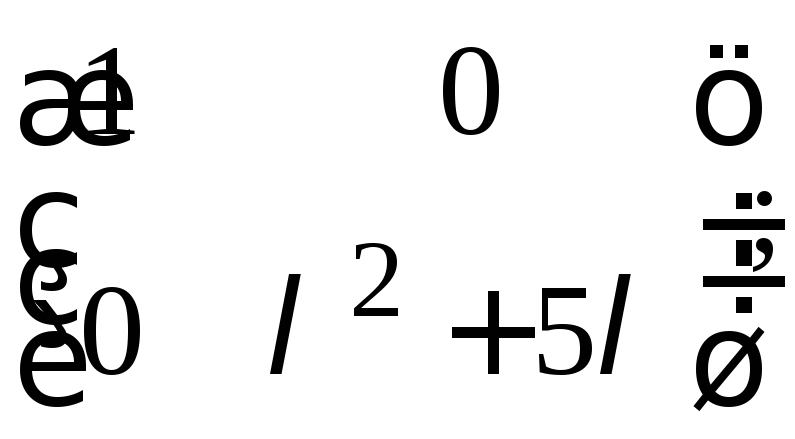
г)
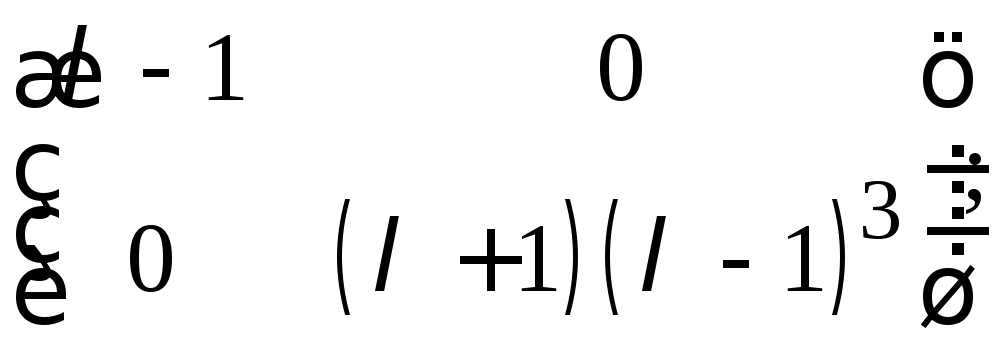
д)

е)
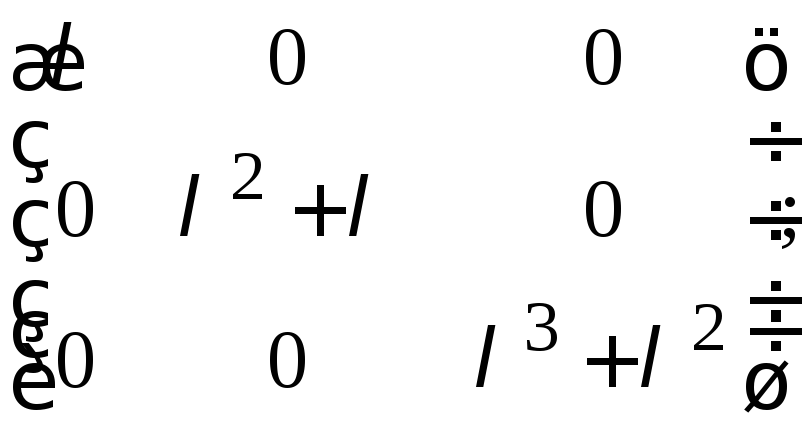
ж)

з)

и)
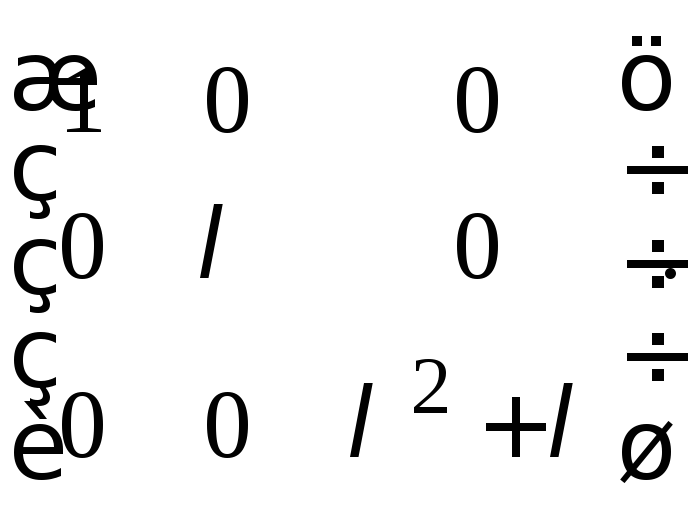
23.
а)
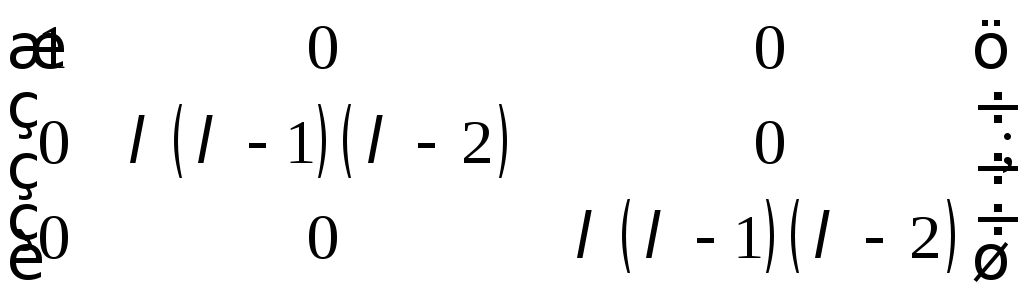
б)

в)

24.
а)

б)

в)
 где
где![]() порядок данной матрицы.
порядок данной матрицы.
г)
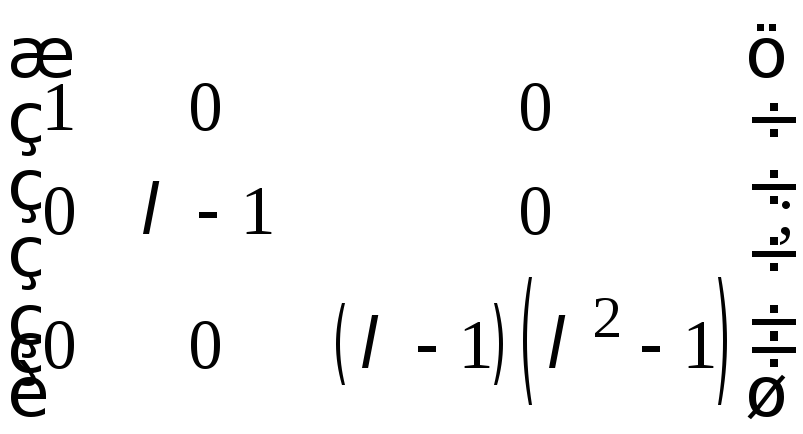
д)

е)
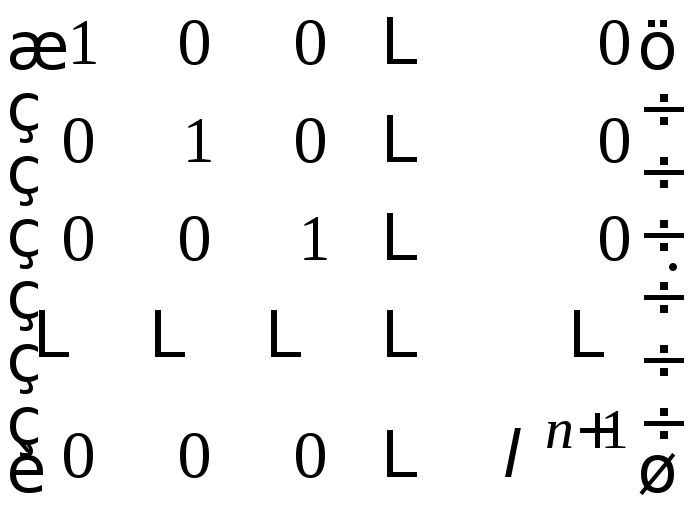
25.
а) эквивалентны;
б) не эквивалентны;
в) матрицы
![]() и
и![]() эквивалентны между собой и не эквивалентны
матрице
эквивалентны между собой и не эквивалентны
матрице![]() .
.
26.
а)
![]()
б)
![]()
в) элементарных делителей не существует.
27.
а)

б)
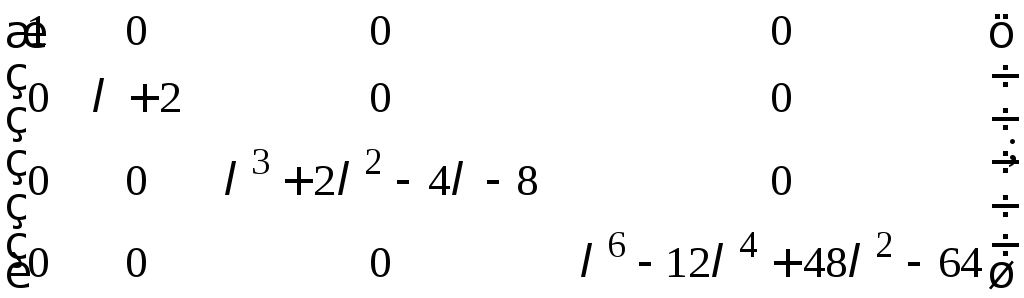
в)

28.
а) подобны;
б) подобны;
в) матрицы
![]() и
и![]() подобны между собой, но не подобны
матрице
подобны между собой, но не подобны
матрице![]() ;
;
г) матрицы
![]() и
и![]() подобны между собой, но не подобны
матрице
подобны между собой, но не подобны
матрице![]() .
.
29.
а)

б)

в)

г)

д)

е)

ж)

з)

и)

к)

л)

м)

н)

о)

п)

30.
а) в поле рациональных
чисел подобна матрице

б)
в поле
вещественных чисел подобна матрице

в) в поле комплексных
чисел подобна матрице

г) не подобна диагональной матрице ни в каком поле.
31.
а)
![]()
б)
![]()
СПИСОК ЛИТЕРАТУРЫ.
Апатенок Р. Ф., Маркина Л. М., Хейнман В. Б. Сборник задач по линейной алгебре и аналитической геометрии. Минск: Высшая школа, 1990.
Ильин В. А., Позняк Э. Г. Линейная алгебра: Учеб.: Для ВУЗов. М.: Физматлит, 2001.
Курош А. Г. Курс высшей алгебры. М.: Наука, 1971.
Проскуряков И. В. Сборник задач по линейной алгебре. М.: Наука, 1984.
Шипачёв В. С. Задачник по высшей математике: Учеб. пособие для ВУЗов. М.: Высшая школа, 2002.
СОДЕРЖАНИЕ.
