§3.2. Унимодулярные -матрицы.

Второй критерий эквивалентности.

матрица называетсяунимодулярной, если она имеет матрицу своим каноническим видом, т. е. если все ее инвариантные множители равны единице.

ТЕОРЕМА 1. матрица тогда и только тогда унимодулярная, если ее определитель отличен от нуля, но не зависит от , т. е. является отличным от нуля числом из основного поля.

ДОКАЗАТЕЛЬСТВО. Если , то этим двум матрицам соответствует один и тот же многочлен. Однако для единичной матрицы. Отсюда следует, что определитель матрицы, отличающийся отлишь отличным от нуля числовым множителем, будет отличным от нуля числом из поля.

Обратно, если определитель матрицы отличен от нуля и не зависит от , то для этой матрицы многочлен будет равен, а т. к.то все инвариантные множителиматрицы,равны единице. □

СЛЕДСТВИЕ 1. Всякая невырожденная числовая матрица является унимодулярной матрицей. □

Пример 2. матрица

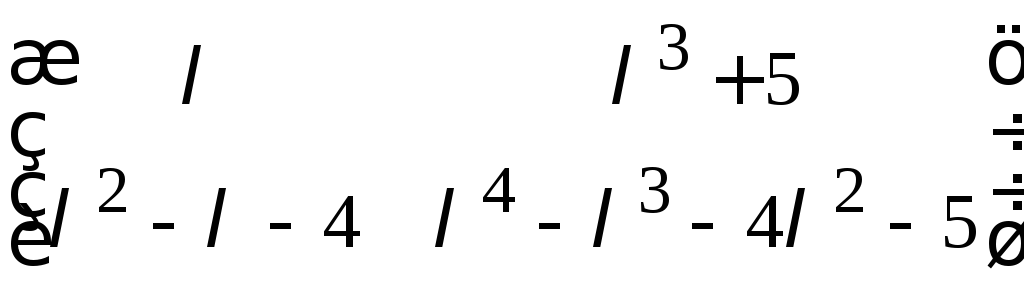
является унимодулярной, действительно, ее определитель равен 20, т. е. отличен от нуля и от не зависит.

СЛЕДСТВИЕ 2. Произведение унимодулярных матриц само унимодулярно.

ДОКАЗАТЕЛЬСТВО следует из теоремы о произведении определителей. □

ТЕОРЕМА 2. матрицатогда и только тогда унимодулярна, когда для нее существует обратная матрица, также являющаясяматрицей.

ДОКАЗАТЕЛЬСТВО. Действительно, если дана невырожденная матрица, то, разыскивая обычным способом обратную матрицу, мы должны будем делить алгебраические дополнения к элементам данной матрицы на определитель этой матрицы, т. е. на некоторый многочлен от . Поэтому в общем случае элементы обратной матрицы будут рациональными дробями от , а не многочленами от , т. е. эта матрица не будет матрицей. Если же дана унимодулярная матрица, то делить алгебраические дополнения придется лишь на отличное от нуля число из поля Р, т.е. элементы обратной матрицы будут многочленами от и поэтому обратная матрица сама будет матрицей. Обратно, если матрица обладает обратной матрицей , то определители этих обеих матриц являются многочленами от , их произведение равно , а поэтому оба определителя должны быть многочленами нулевой степени. □

СЛЕДСТВИЕ 3. матрица, обратная к унимодулярнойматрице, сама унимодулярна. □

Назовем элементарной матрицей числовую (и, следовательно, ) матрицу вида (1) или (2):

(1)

отличающуюся от единичной матрицы лишь тем, что на некотором ом месте главной диагонали,, стоит произвольное числоиз поля, отличное от нуля;

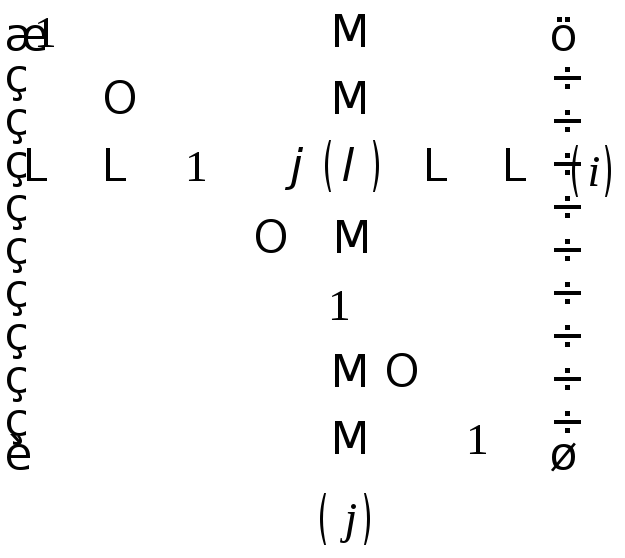(2)

отличающуюся от единичной матрицы лишь тем, что на пересечении ой строки иого столбца,,причем, стоит произвольный многочлениз кольца.

УТВЕРЖДЕНИЕ 1. Всякая элементарная матрица унимодулярна.

ДОКАЗАТЕЛЬСТВО. В самом деле, определитель матрицы (1) равен , но, по условию,; определитель же матрицы (2) в точности равен. □

УТВЕРЖДЕНИЕ 2. Выполнение в матрицелюбого элементарного преобразования равносильно умножению этой матрицы слева или справа на некоторую элементарную матрицу.

ДОКАЗАТЕЛЬСТВО. Действительно, очевидна справедливость следующих четырех утверждений:

1) умножение матрицы слева на матрицу (1) равносильно умножению ой строки матрицы на число ;

2) умножение матрицы справа на матрицу (1) равносильно умножению ого столбца матрицы на число ;

3) умножение матрицы слева на матрицу (2) равносильно прибавлению к ой строке матрицы ее ой строки, умноженной на;

4) умножение матрицы справа на матрицу (2) равносильно прибавлению к ому столбцу матрицы ее ого столбца, умноженного на. □

УТВЕРЖДЕНИЕ 3. матрица тогда и только тогда унимодулярна, когда она представила в виде произведения элементарных матриц.

ДОКАЗАТЕЛЬСТВО. Произведение элементарных матриц, как частного случая унимодулярных, само унимодулярно.

Обратно, если матрица является унимодулярной, то, т. е. отможно перейти кс помощью конечного числа элементарных преобразований. Заменяя каждое из этих преобразований умножением слева или справа на элементарную матрицу, мы придем к равенству

,

где все матрицы элементарны. □

ТЕОРЕМА 3. (второй критерий эквивалентности матриц).Две матрицыипорядкатогда и только тогда эквивалентны, когда существуют такие унимодулярныематрицыитого же порядка, что

(3)

ДОКАЗАТЕЛЬСТВО. Оно аналогично доказательству предыдущего утверждения. Так как , то отможно перейти кпри помощи конечного числа элементарных преобразований, т. е.

(4)

где матрицы элементарны и, следовательно, унимодулярны. Унимодулярными будут, поэтому и матрицы

(5)

являющиеся произведениями унимодулярных матриц, а равенство (4) перепишется в виде (3). Заметим, что если, например, , т. е. элементарные преобразования совершались лишь над столбцами, то полагаем просто.

Обратно, пусть для матриц исуществуют такие унимодулярные матрицы и , что имеет место равенство (3). По доказанному, матрицы и можно представить в виде произведений элементарных матриц; пусть это будут представления (5). Равенство (3) перепишется теперь в виде (4) и, заменяя каждое умножение на элементарную матрицу соответствующим элементарным преобразованием, мы получим, наконец, что . □