§1.2. Изоморфизм унитарных пространств.

Два унитарных (или евклидовых) пространства иназываютсяизоморфными, если между их элементами можно установить взаимно однозначное соответствие , для которого

и .

ТЕОРЕМА. (об изоморфизме унитарных пространств). Два унитарных пространства изоморфны тогда и только тогда, когда они имеют одинаковую размерность.

ДОКАЗАТЕЛЬСТВО. Очевидно, что если иизоморфны, то они являются изоморфными, как линейные пространства. Однако изоморфные линейные пространства имеют одинаковую размерность [1].

Обратно, пусть размерности иравны, а и, соответственно, их ортонормированные базисы. Зададим отображениеследующим образом: если

,

то считаем

.

Это отображение взаимнооднозначно и сохраняет операции сложения и умножения на число. Значит, они изоморфны, как линейные пространства.

Покажем, что сохраняет скалярное произведение. Рассмотрим два произвольных вектора

,

.

Тогда

и

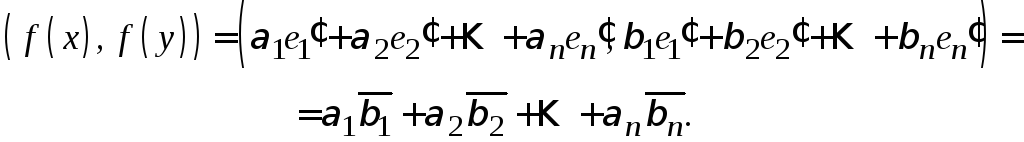
То есть . □

§1.3. Линейные функции.

Рассмотрим произвольное линейное пространство над полем. Отображениеназываетсялинейной функцией, если

Нетрудно проверить, что если илинейные функции, тои, такие чтои, так же являются линейными функциями. Поэтому, множество всех линейных функций, заданных вобразуют линейное пространство относительно их сложения и умножения числа на функцию.

ЛЕММА. (о существовании и единственности линейной функции). Для любого базиса линейного пространства и любого набора существует единственная линейная функция, такая, что

.

ДОКАЗАТЕЛЬСТВО. Пусть произвольный вектор из . Зададим отображениеследующим образом:

,

Очевидно, что .

Проверим, что линейная функция. Пусть . Тогда

.

Докажем единственность. Предположим, что существует другая линейная функция , удовлетворяющая условию леммы, т. е.

. Тогда .□

Пусть унитарное пространство. Положим по определениюдля любыхи фиксированного. Тогда имеет место

ТЕОРЕМА. Функция является линейной и однозначно определяется по . Обратно, для каждой линейной функциисуществует элемент , такой что .

ДОКАЗАТЕЛЬСТВО. Вначале докажем линейность функции. Действительно

.

Пусть теперь , тогда. Приимеем, т. е.. Тем самым показано, что каждомусоответствует единственная линейная функция.

Наконец, пусть произвольная линейная функция, заданная в пространстве . Докажем, что существует элемент, такой, чтодля любых. Пустьортонормированный базис пространства. По лемме, существует единственный набор , такой, что . Рассмотрим вектор

,

тогда . Для произвольного вектора, имеем

. □

§1.4. Сопряжённые операторы.

Построим по каждому линейному оператору мерного унитарного пространства оператор, сопряжённый данному. Выберем ввектори рассмотрим функциюпеременной. Эта функция является линейной. Действительно

С другой стороны , гдепо теореме из предыдущего параграфа определяется однозначно по функции, т. е. пои. Таким образом, при фиксированном для каждогоимеется единственный вектор. Операторназываетсясопряжённым к , т. е.

Покажем, что для каждого сопряжённый оператор определяется однозначно. Предположим, что существует оператор, такой что, тогда

.

Нетрудно убедиться в том, что сопряжённый оператор является линейным. Действительно

.

Значит .

Отметим следующие свойства сопряжённого оператора:

1. ;

2. ;

3. ;

4. .

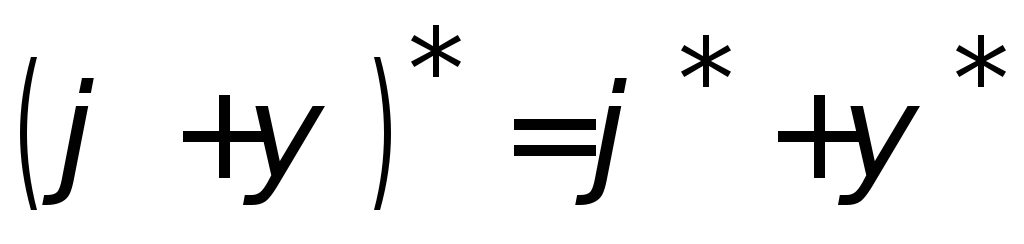Докажем первое свойство.

. Другие свойства доказываются аналогично.

Если квадратная матрица порядка, то матрица, полученная иззаменой всех её элементов на комплексно-сопряжённые и последующим её транспонированием, называетсясопряжено транспонированной. Т. е. если , то.

ТЕОРЕМА. Если линейный оператор в ортонормированном базисе имеет матрицу , то сопряжённый оператор будет иметь в этом базисе сопряжено транспонированную матрицу.

ДОКАЗАТЕЛЬСТВО. Пусть в унитарном пространстве задан ортонормированный базис , а матрицы операторов ив этом базисе будут соответственно, т. е. для любых

;

.

Домножим первое равенство справа на , получим

, следовательно .□

Пример 1. Линейный оператор задан в евклидовом пространстве в базисе из векторовматрицей

.

Найти матрицу сопряжённого оператора в том же базисе, считая, что координаты векторов базиса даны в некотором ортонормированном базисе.

Решение. Координаты векторов заданы в некотором ортонормированном базисе. Матрица перехода откбудет

.

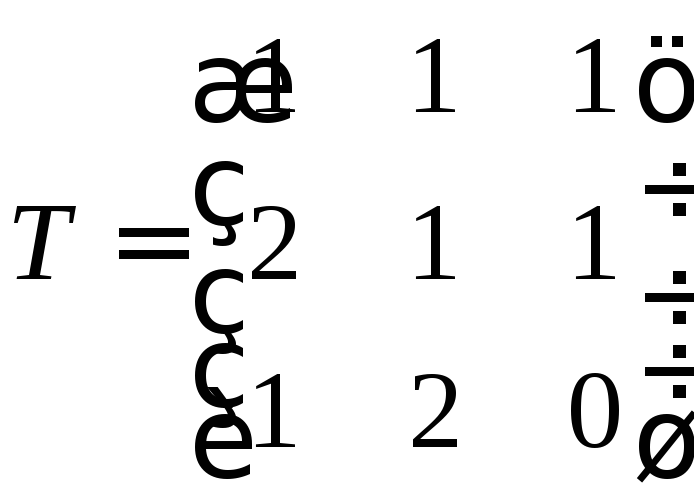Значит, , гдематрица того же оператора в ортонормированном базисе. Откуда.

Находим

.

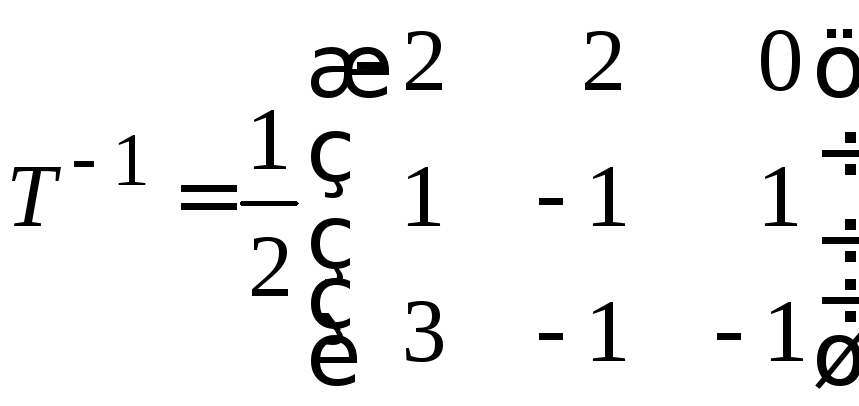Тогда

.

Матрица сопряжённого оператора будет по предыдущей теореме сопряжено транспонированной, а так как оператор задан в евклидовом пространстве, то просто транспонированной.

.

Возвращаемся к исходному базису