§1.5. Нормальные операторы.

Линейный оператор унитарного пространстваназываетсянормальным, если

,

т. е. если он перестановочен со своим сопряжённым.

Если ортонормированный базис пространства иматрица нормального операторав этом базисе, то по теореме из§1.3 имеем .

Справедливы следующие три теоремы о нормальных операторах.

ТЕОРЕМА 1. Всякий собственный вектор нормального оператора , соответствующий собственному значению будет и собственным вектором оператора, который соответствует комплексно-сопряжённому значению.

ДОКАЗАТЕЛЬСТВО. Если линейный оператор, атождественный оператор, тотакже линейный оператор, сопряжённым для которого будет(т. к.). По условиюнормальный оператор, значит. Нетрудно проверить, что

.

Из того, что является собственным вектором оператора следует, что, значит

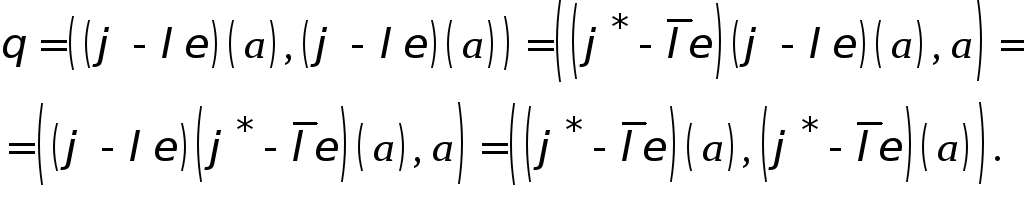
То есть и. □

ТЕОРЕМА 2. Собственные векторы, соответствующие различным собственным значениям нормального оператора будут ортогональны.

ДОКАЗАТЕЛЬСТВО. Пусть .

Тогда

.

Откуда , следовательно, т. к.. □

ТЕОРЕМА 3. (основная о нормальных операторах). Для каждого нормального оператора в унитарном пространстве найдётся ортонормированный базис, составленный из собственных векторов оператора . Матрица имеет в этом базисе диагональный вид.

ДОКАЗАТЕЛЬСТВО. Пусть характеристический корень линейного оператора(по основной теореме алгебры комплексных чисел [3] такой корень существует). Ему соответствует собственный вектор. Рассмотрим множество, которое является подпространством пространстваи называетсяортогональным к . Так как, то для любого векторасправедливо

.

Таким образом, как только. Такое подпространство называетсяинвариантным, относительно оператора .

Рассмотрим оператор , заданный наследующим образом:. Оно называетсяограничением на . Заметим, что собственные векторыбудут собственными векторами и.

Далее аналогично находим в собственный вектороператора. Пустьподпространство векторов, ортогональных ки.будет опять инвариантным относительно, т. к. является пересечением двух инвариантных подпространств. В нём снова найдётся собственный вектороператора. И т. д.

Продолжая указанную процедуру, получим ортогональный базис пространства, составленный из собственных векторов оператора. Остаётся нормировать этот базис.

В этом базисе матрица линейного оператора будет иметь диагональный вид [2]. □

§1.6. Унитарные операторы.

Линейный оператор унитарного пространстваназываетсяунитарным, если он сохраняет скалярное произведение векторов, т. е.

.

Непосредственно из определения унитарного оператора следует:

,

т. е. тождественный оператор. Следовательно, унитарный оператор можно определить как оператор, для которого.

Так как , заключаем, что унитарный оператор является частным случаем нормального оператора.

Если матрица операторав некотором ортонормированном базисе, то матрицабудетсопряжено транспонированной. Условие унитарности операторав матричной форме будет выглядеть следующим образом:или. Такая матрицатоже называетсяунитарной.

Если линейный оператор рассматривается в евклидовом пространстве и сохраняет скалярное произведение, то его матрица в некотором базисе будет такой, что , т. е. транспонированная матрица совпадает с обратной. Такой оператор называютортогональным, а его матрицу ортогональной.

ТЕОРЕМА 1. Линейный оператор унитарного пространстваявляется унитарным тогда и только тогда, когда он сохраняет длину вектора, т. е..

ДОКАЗАТЕЛЬСТВО. Действительно,

.

В другую сторону, пусть . Тогда для любогосправедливо:. Если сохраняет скалярное произведение, то . Раскрывая скобки и учитывая, чтои, получим

(1)

При получаем

(2)

В случае евклидова пространства, т. к. , имеем.

Иначе, положим в (1) , получим

.

Прибавим полученное равенство к (2), тогда . □

ТЕОРЕМА 2. Линейный оператор унитарного пространстваявляется унитарным тогда и только тогда, когдапереводит любой ортонормированный базис этого пространства снова в ортонормированный.

ДОКАЗАТЕЛЬСТВО. Пусть ортонормированный базис пространства . По определению унитарного пространства , значит,. А по предыдущей теореме.

Обратно, пусть

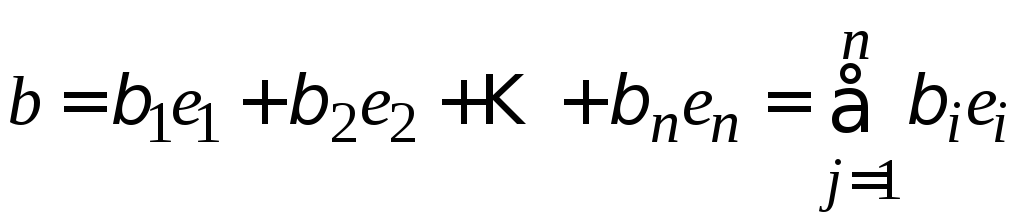, , тогда. Так как по предположению переводит ортонормированный базис в ортонормированный, то

.

Следовательно, унитарный оператор. □

ТЕОРЕМА 3. (основная об унитарных операторах). Матрица унитарного оператора в подходящем ортонормированном базисе является диагональной, с диагональными элементами, равными по модулю единице.

ДОКАЗАТЕЛЬСТВО. Так как является частным случаем нормального оператора, то по основной теореме о нормальных операторах, в некотором ортонормированном базисе он задаётся диагональной матрицей. Покажем, что собственные значения по модулю равны 1.

Пусть . тогда

.

Но , т. е.. Значит,, т. е.. □