2). Размещение модулей на мкп

- процесс установки модулей i-того ранга на МКП модуля (i+1)-го ранга с оптимизацией качества размещения.

Считается, что координата условного центра модуля совпадает с узлом сетки размещения на МКП и соблюдается условие

i,j  {1,2,3,…k} i ≠ j и PiPj = 0,

где Pi и Pj – номера установочных мест на МКП.

Для регулярного МКП число возможных вариантов размещений равно

K!

R = ----------------- , где

(K – N)

K – число установочных позиций на МКП, K  N при условии, что один модуль занимает одну установочную позицию.

Заметим, что для цифровых устройств необходимо минимизировать временные задержки сигналов между модулями. Если предположить что задержки сигнала пропорциональны расстоянию между источником и приемником сигнала, то показатель оптимальности размещения в этом случае можно записать в виде

L = d_ijf  Lmin, где

d_ijf - расстояние между элементами x_i и x_j, соединенных цепью t_f.

3). Трассировка соединений и выпуск КТД - пояснить.

Алгоритмы и модели компоновки ву

Обычно задачи компоновки рассматриваются как процесс принятия решений в определенных или неопределенных условиях, в результате выполнения которого исходные модули (элементы схемы) ВУ назначаются в блоки i-го уровня. В свою очередь, эти элементы назначаются в блоки (i+1)-го уровня и т. д., причем расположение выполняется с учетом выбранного критерия компоновки.

Под задачей компоновки ВУ понимается задача объединения модулей низшего (i— 1)-го уровня в модули более высокого i-го уровня по заданному критерию (или набору критериев) оптимизации и при наличии заданных ограничений.

Среди методов компоновки ВУ выделяют два характерных класса.

К первому классу относятся такие алгоритмы, в которых осуществляется разбиение КС на части (блоки) с учетом таких ограничений, как число элементов в блоках, число внешних выводов блоков, суммарная площадь, занимаемая элементами и соединениями, и т. д. Основными критериями для такого разбиения являются следующие критерии:

• число W образующихся блоков Gg, g=1,W;

• число внешних выводов на блоках K_gдоп;

• задержки в распространении сигналов;

• электромагнитная и тепловая совместимость элементов и т. д.

Задачи такого вида возникают при разбиении КС на блоки большей степени сложности, к которым не предъявлены требования в отношении их схемной унификации. Это задачи распределения блоков по панелям, микросборок по печатным платам, разбиение КС на БИС, СБИС. К первому классу задач компоновки относят такие, в которых критерии оптимизации и ограничения могут быть сведены к определенным конструктивным параметрам расположения отдельных элементов и их межсоединений. Эти задачи называются задачами компоновки конструктивных частей (блоков).

Второй класс алгоритмов компоновки образуют такие методы, в которых кроме конструктивных характеристик образующихся блоков существенны и их функциональные характеристики. Они возникают на этапе перехода от функциональных (логических) схем ВУ к электрической схеме, ориентированной на заданную систему элементов. Компоновка состоит в назначении элементов логической схемы в типовые модули из заданного набора. Указанный класс называют методом покрытия или задачами компоновки типовых блоков. Основными критериями при покрытии схем являются следующие:

• число модулей, необходимых для покрытия исходной схемы;

• число межмодульных соединений;

• число типов используемых модулей;

• число неиспользованных элементов во всех модулях схемы и т. д.

В качестве ограничений выступают конструктивные и функциональные характеристики типовых модулей, такие как:

• максимально допустимое число модулей (i-1)-го ранга в модулях i-го ранга;

• максимально допустимое число выводов формируемого модуля K_gдоп;

• ограничения на совместную работу модулей одного уровня и т.д.

Основным при компоновке является критерий электромагнитной и тепловой совместимости элементов низшего уровня. Он определят область допустимых разбиений схемы, на которой формулируются другие критерии. Такими критериями могут быть:

• число типов конструктивно законченных частей;

• заполнение конструктивной части высшего уровня элементами низшего уровня;

• число соединений между конструктивными частями;

• простота диагностирования схем и др.

Очевидно, что внешние соединения между частями КС являются одним из важнейших факторов, определяющих надежность ВУ. Поэтому наиболее распространенным критерием является суммарное число внешних связей. Реализация этого критерия обеспечивает минимизацию взаимных наводок, упрощение конструкции, повышение надежности и т. д. В связи с этим, рассмотрение методов компоновки КС будет проводиться, в основном, на примере этого критерия.

Исходными данными для решения задачи компоновки ВУ является КС.

Для алгоритмизации и формального решения задачи производится переход от КС к графу, к мультиграфу, к гиперграфу одним из методов, описанных выше.

Наибольшее применение нашли эвристические алгоритмы разбиения. Они позволяют за конечное число шагов получить локальный минимум, который в общем случае является достаточным для практических целей.

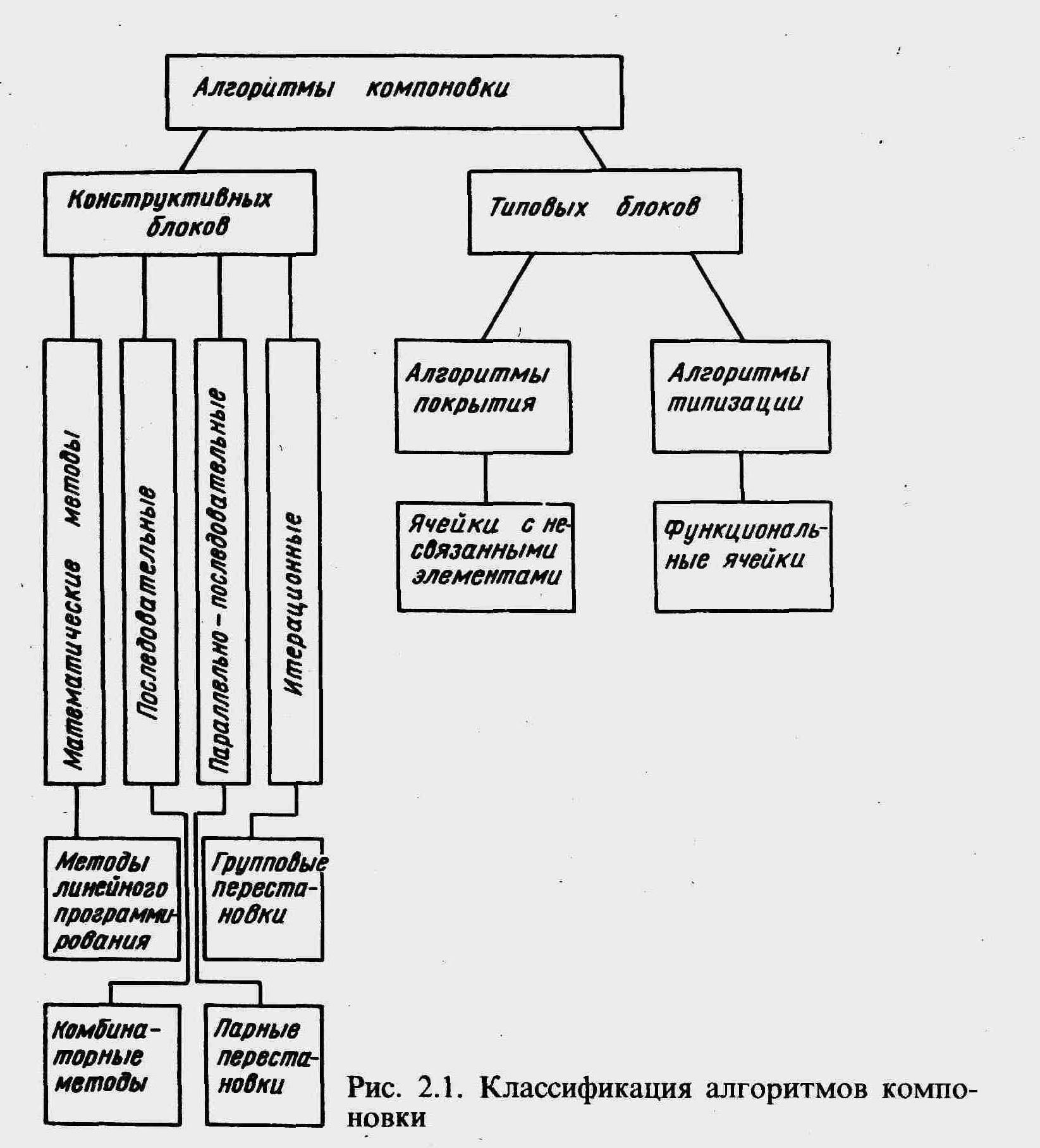
Для указанных классов задач компоновки выделяют алгоритмы компоновки конструктивных и типовых блоков. Известная классификация таких алгоритмов показана на рис. 2.1.

Алгоритмы классифицируются по критериям, по ограничениям на формирование частей или по структуре вычислительной процедуры. С этой точки зрения их делят на последовательные, параллельно-последовательные и итерационные.

В алгоритмах первого типа вводится последовательный процесс компоновки блоков, на каждом шаге которого в очередной блок добавляется один из модулей схемы, выбираемый по определенному приоритету.

В параллельно-последовательных алгоритмах сначала выделяется некоторое исходное множество групп элементов, которое затем распределяется по блокам с учетом критериев и ограничений на компоновку. Обычно эти алгоритмы используются при решении задач компоновки со специальными требованиями (например, минимизация числа разнотипных блоков) и обладают более сложной структурой. Алгоритмы этих двух типов применяются для создания базового (начального) варианта компоновки.

Ите­рационные алгоритмы служат для улучшения некоторого началь­ного варианта компоновки в соответствии с принятым критерием.

При использовании итерационных алгоритмов сначала граф разбивается на определенное число блоков произвольным образом, например с помощью последовательных алгоритмов. Затем по некоторым правилам производится перестановка вершин из одного блока в другой с целью минимизации числа внешних ребер.

В алгоритмах разбиения, основанных на математических методах, в основном используются методы ветвей и границ и задачи о назначении. Алгоритмы разбиения с применени­ем методов ветвей и границ состоят из следующих этапов. Сначала определяется нижняя оценка разбиения графа на заданное число частей. Затем производится построение дерева решений и осуществляется поиск оптимального результата.

Задачу разбиения графа схемы на блоки можно свести к задаче о назначении. При этом ищется назначение кандидатов (вершин графа) на все блоки, дающие минимальные суммарные затраты. Причем каждая вершина графа может быть назначена только в один блок и в каждом блоке должны содержаться различные вершины графа.

Алгоритмы компоновки типовых блоков сводятся к так называемым задачам покрытия и типизации. Под покрытием понимается представление функциональной схемы ЭВА типовыми конструктивными элементами, на которых она будет реализована, и связями между ними с выполнением заданных КО.

При покрытии выделяют задачи с несвязанными элементами и фун­кциональными ячейками. В первом случае решают задачи опре­деления необходимого числа ячеек для покрытия КС с минималь­ной суммарной стоимостью и минимизации числа связей между ячейками. Во втором случае решают задачи покрытия КС заданным классом функциональных ячеек с минимизацией числа ячеек и суммарного числа межъячеечных связей.

Типизация—это разбиение КС на блоки по критерию опти­мальности—минимуму номенклатуры частей разбиения или по критерию оптимальности — максимуму однотипности использу­емых ячеек. Отметим, что сокращение номенклатуры ТЭК позволяет уменьшить затраты на дальнейшее проектирование.