- •Компьютерные технологии проектирования вычислительных устройств
- •Структура сапр
- •1. Математические модели конструкций и схем ву
- •Модель компонента
- •Модели электрических схем
- •Компьютерные технологии проектирования печатных плат в среде p-cad Создание символов компонентов
- •Конструкторско-технологические параметры печатных плат
- •Отверстия печатных плат
- •Стеки контактных площадок (Pad Stacks) и переходных отверстий (Via Stacks).
- •Создание на пп посадочных мест компонентов.
- •Создание схемы электрической принципиальной
- •2). Размещение модулей на мкп
- •Алгоритмы и модели компоновки ву
- •Критерии оптимизации при разрезании электрической схемы
- •1 , Если tf t(xj)
- •Итерационный алгоритм разбиения гиперграфа
- •Пример алгоритма типизации.
- •Покрытие функциональных схем модулями заданного библиотечного набора
- •Задача размещения модулей.
- •Размещение компонентов в регулярном монтажном пространстве
- •Размещение компонентов в нерегулярном монтажном пространстве
- •Алгоритм последовательного размещения
- •Метод силовых функций (непрерывно – дискретный алгоритм размещения)
- •Задача "перераспределения" выводов модуля
- •Подсчет изменения суммарной длины связей в итерационных алгоритмах
- •Трассировка электрических соединений
- •Математическая формулировка задачи трассировки электрических соединений.
- •Алгоритмы трассировки
- •Эвристический алгоритм трассировки. Двухлучевой алгоритм трассировки
Эвристический алгоритм трассировки. Двухлучевой алгоритм трассировки
Идея алгоритма состоит в целенаправленном характере отыскания пути между двумя ячейками, т.е. пути в лабиринте, образованном занятыми и свободными ячейками. Время поиска пути при этом существенно сокращается. Обе ячейки (контакта) являются и источником и приемником целенаправленно распространяемой волны в заданных направлениях.
В общем виде алгоритм состоит из следующих шагов:
продвижение в оптимальном (приоритетном) направлении;
определение точки встречи с препятствием;
выбор направления обхода препятствия;
обход препятствия;
определение точки встречи двух лучей.
Указанные шаги приводят либо к встрече двух лучей, либо к точке, продвижение из которой невозможно. Возникают ситуации "тупик" и "блокировка".
"Тупик" – ситуация, при которой в окрестности очередной ячейки нет свободных ячеек, и необходим возврат на некоторое число ячеек (шагов) назад для поиска обходного пути.
"Блокировка" – ситуация, в которой при выбранном (разрешенном) направлении обхода препятствия искомый путь построить нельзя и требуется отыскать другое направление обхода препятствия.
В двухлучевом алгоритме от каждой конечной ячейки распространяется по два луча: от точки А лучи А1 и А2, а от точки В лучи В1 и В2. Трассу можно провести только в том случае, если оба луча сошлись (встретились) в одной точке.
Для определения приоритетных направлений распространения лучей используются псевдобулевы переменные;
{
{
1, если (za –zb) 0,
=
0, если (za – zb) < 0
{
1, если (ya – yb) 0,
=
0, если (ya – yb) <0,
где z и y – горизонтальная и вертикальная координаты.
|
Схема распространения лучей | |||
|
= 0, = 0 |
= 1, = 0 |
|
= 1, = 1 |
|
В2 В А1
В1
А А2
В2 В А1
В1
А А2
В2 В А1
В1
А А2
В2 В А1
В1
А А2
В2 В А1
В1
А А2
В2 В А1
В1
А А2
В2 В А1
В1
А А2
В2 В А1
В1
А А2 |
В2 В
А1 В1
А А2
В2 В
А1 В1
А А2
В2 В
А1 В1
А А2
В2 В
А1 В1
А А2
В2 В
А1 В1
А А2
В2 В
А1 В1
А А2
В2 В
А1 В1
А А2
В2 В
А1 В1
А А2 |
А
А2
А1
В1
В2 В А
А2
А1
В1
В2 В А
А2
А1
В1
В2 В А
А2
А1
В1
В2 В А
А2
А1
В1
В2 В А
А2
А1
В1
В2 В А
А2
А1
В1
В2 В А
А2
А1
В1
В2 В |
А2 А
В1
А1
В В2
А2 А
В1
А1
В В2
А2 А
В1
А1
В В2
А2 А
В1
А1
В В2
А2 А
В1
А1
В В2
А2 А
В1
А1
В В2
А2 А
В1
А1
В В2
А2 А
В1
А1
В В2 |
Графически разрешенные направления распространения лучей можно представлены выше в виде Таблицы.
Для исключения блокировки лучей алгоритм приходится усложнять с целью вывода луча из тупиков. Для этого луч из заблокированной ячейки возвращается назад, в соседнюю ячейку, из какой луч пришел раньше, и предпринимается попытка провести луч по второму направлению и т.д. (При этом все просмотренные элементы (блокированные ячейки) считаются запрещенными для данного луча).
После выхода луча из тупика – при N шагах возврата – для выравнивания длины всех лучей требуется выполнить N+1 дополнительных шагов распространения для луча, выведенного из тупика.
Дать Примеры: двухлучевого алгоритма
и алгоритма Прима.
Канальные алгоритмы трассировки основаны на проложении трасс по укрупнённым дискретам КП, в качестве которых служит система горизонтальных и вертикальных каналов. Ширина каждого канала зависит от числа прокладываемых в них соединений.
Канал разбивается на линейки, называемые магистралями. Любое соединение при канальной трассировке будет представлять совокупность объединенных в одну цепь участков магистралей.
Реализация канального алгоритма предполагает выполнение двух процедур:
- распределение соединений по каналам с учетом их оптимальной загрузки
- и оптимизация расположения соединений на магистралях каналов.
Для заданной конструктивно-технологической базы изготовления печатных плат каждому каналу монтажной плоскости можно поставить в соответствие число, называемое пропускной способностью канала и обозначающее максимальное допустимое число проводников, проходящих через сечение канала с выполнением технологических ограничений. При этом процедура оптимального распределения соединений по каналам в простом случае сводится к их равномерной загрузке, а в более сложных случаях, кроме того, осуществляется учет электромагнитной и тепловой совместимости соседних проводников.
Целью выполнения второй процедуры — оптимизации расположения соединений на магистралях каналов — является минимизация числа переходных отверстий с одного слоя монтажной плоскости на другой.
Задачи первой процедуры решаются с помощью алгоритмов построения КПД. В процессе построения КПД для каждого соединения учитывается загрузка каждого из каналов, через которые оно проходит. По окончании построения КПД для каждой из цепей определяется фактическая загрузка для каждого канала и сравнивается с соответствующей пропускной способностью Yi. Если zi > Yi, то m цепей (где m = zi — Уi) подлежат перетрассировке, причем с использованием только тех каналов, для которых zj < Yj.
Другой подход предполагает учет текущей пропускной способности каналов Yi, т. е. числа проводников, которые еще можно проложить на этом участке. Канал «закрывается» для размещения соединений, как только Yi = 0.
Часто для распределения соединений по каналам вместо процедур построения КПД используются волновые процедуры, при этом дискретами для распространения волны на КП являются каналы.
Задача окончательной трассировки обычно формулируется следующим образом. Дан горизонтальный канал, ограниченный верхним и нижним рядами контактов соответственно PTi, PTj, где i, j = 1, 2, ... Между верхним и нижним рядами заданы множества свободных линий, магистралей: S = {Sk} k=l, 2, ..., m}, где m—ширина канала. Необходимо в общем случае ломаными линиями, проходящими по участкам магистралей, соединить все абсциссы одноименных групп контактов (каждая группа соответствует одной и той же цепи), затем вертикальными отрезками соединить контакты. Трассировку следует производить по выбранному критерию качества (суммарная длина, число межслойных переходов, реализованных соединений, занятых магистралей и т. д.).
Следует отметить, что канальные алгоритмы тем перспективнее, чем больше размерность решаемых задач.
Класс канальных алгоритмов трассировки отличается от волновых повышенным быстродействием, меньшим расходом памяти ЭВМ, однако он менее универсален, что накладывает определенные ограничения на класс конструктивно-технологических решений. В волновые, лучевые и в меньшей мере в канальные алгоритмы заложен последовательный принцип трассировки, что предполагает оптимальное построение каждой отдельной трассы без прогноза на прокладку последующих соединений на монтажной плоскости. Недостаток этого принципа проявляется по мере приближения к концу решения задачи, когда, как правило, становится очевидным тот факт, что отдельные ранее проложенные трассы можно было бы построить не оптимально, но при этом возникли бы дополнительные возможности к прокладке ряда последующих трасс.
Приемы неавтоматизированного проектирования, применяемые опытными конструкторами, привели к созданию метода «гибкой» трассировки, характеризующегося отсутствием жесткой фиксации прокладываемых трасс, которые при наличии таковой часто создают необоснованные препятствия для еще непроложенных трасс.
Метод гибкой трассировки состоит из двух основных этапов:
Макротрассировки (строится оптимальная топологическая модель для всех трасс, что обеспечивает их плоское вложение в ДТРП);
микротрассировки (строятся геометрические модели для каждой трассы).
Иначе говоря, на первом этапе цепи размещаются в довольно крупные области, в пределах которых они могут «плавать», создавая оптимальные условия для прокладки других соединений.
А на втором этапе происходит фиксация соединений на монтажном пространстве с определением их геометрических характеристик.
Для определения моделей топологии отдельных цепей разработаны специальные процедуры на основе задачи определения КПД на КП. Достаточно высокое быстродействие построения может быть достигнуто применением волновых методов.
В процессе построения КПД учитываются только топологические препятствия, а основные метрические параметры КП (например, пропускные способности узких промежутков) выступают как ограничения. Основными процедурами на этапе макротрассировк являются распространение и свертывание волны, модификации и стирание модели топологии. Этим обеспечивается реализации различных стратегий трассировки. При трассировке многослойных структур возможна организация процедуры распространения объемной волны.
Отметим, что модель топологии задает длину трассы в пределах, определяемых «коридором», отведенным для этой цепи, и может колебаться в результате микротрассировки от lmin до lmax.
Как было указано выше, на этапе микротрассировки определяются геометрические характеристики каждой трассы: конфигурация трассы, суммарное число изгибов всех трасс, а так же для каждой трассы в отдельности точные координаты всех характерных точек трасс, ширина трасс и т.д. Ограничением в данном случае является информация, полученная на предыдущем этапе, где все фрагменты трасс распределены по макродискретам. Микротрассировка осуществляется оптимальным "включением" моделей топологии трасс в двумерное евклидово пространство.
При этом трассы обычно сводят в три основные группы:
- с произвольной конфигурацией;
- проходящие по двум взаимно ортогональным направлениям;
- реализуемые в макродискретном рабочем поле.
Прокладка проводников в алгоритмах гибкой трассировки осуществляется последовательно, однако ранее проложенные трассы не закрепляются «жестко», что создает благоприятные условия для прокладки последующих соединений. Кроме того, представление монтажной плоскости в виде системы граней оказывается удобным для конструкций, использующих разногабаритные элементы.
Основной недостаток гибкой трассировки — сложность алгоритма, а вследствие этого имеют место большие затраты памяти ЭВМ и времени на получение решения.
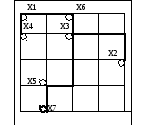
Пример алгоритма Прима
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
0 |
6 |
3 |
1 |
4 |
2 |
5 |
21 |
|
2 |
6 |
0 |
3 |
5 |
4 |
4 |
5 |
27 |
|
3 |
3 |
3 |
0 |
2 |
3 |
1 |
4 |
17 |
|
4 |
1 |
5 |
2 |
0 |
3 |
3 |
4 |
18 |
|
5 |
4 |
4 |
3 |
3 |
0 |
4 |
1 |
19 |
|
6 |
2 |
4 |
1 |
3 |
4 |
0 |
5 |
19 |
|
7 |
5 |
5 |
4 |
4 |
1 |
5 |
0 |
24 |
А) Таблица расстояний между центрами контактов
Б) Схема проведенных трасс
стр.

 = 0,
= 1
= 0,
= 1