
- •Компьютерные технологии проектирования вычислительных устройств
- •Структура сапр
- •1. Математические модели конструкций и схем ву
- •Модель компонента
- •Модели электрических схем
- •Компьютерные технологии проектирования печатных плат в среде p-cad Создание символов компонентов
- •Конструкторско-технологические параметры печатных плат
- •Отверстия печатных плат
- •Стеки контактных площадок (Pad Stacks) и переходных отверстий (Via Stacks).
- •Создание на пп посадочных мест компонентов.
- •Создание схемы электрической принципиальной
- •2). Размещение модулей на мкп
- •Алгоритмы и модели компоновки ву
- •Критерии оптимизации при разрезании электрической схемы
- •1 , Если tf t(xj)
- •Итерационный алгоритм разбиения гиперграфа
- •Пример алгоритма типизации.
- •Покрытие функциональных схем модулями заданного библиотечного набора
- •Задача размещения модулей.
- •Размещение компонентов в регулярном монтажном пространстве
- •Размещение компонентов в нерегулярном монтажном пространстве
- •Алгоритм последовательного размещения
- •Метод силовых функций (непрерывно – дискретный алгоритм размещения)
- •Задача "перераспределения" выводов модуля
- •Подсчет изменения суммарной длины связей в итерационных алгоритмах
- •Трассировка электрических соединений
- •Математическая формулировка задачи трассировки электрических соединений.
- •Алгоритмы трассировки
- •Эвристический алгоритм трассировки. Двухлучевой алгоритм трассировки
Структура сапр
Технические средства – совокупность применяемых в процесс проектирования компьютеров и периферийного оборудования.
Математическое обеспечение – совокупность математических методов, математических моделей и алгоритмов проектирования.
Информационное обеспечение – совокупность БД и СУБД.
Программное обеспечение – программы алгоритмов проектирования, определяющие назначение и функциональные возможности конкретной САПР.
Лингвистическое обеспечение – совокупность языков проектирования.
Организационное обеспечение – определяет форму представления результатов проектирования и взаимодействие пользователей САПР.
Методическое обеспечение – совокупность документов, устанавливающих состав и правила отбора и эксплуатации средств обеспечения САПР.
1. Математические модели конструкций и схем ву
Конструкторское проектирование является одним из наиболее трудоемких и ответственных этапов всего процесса проектирования сложной ЭВА, имеющей многоуровневое иерархическое деление. При проектировании таких устройств постановка и решение задачи структурной оптимизации сталкиваются с двумя трудностями. Во-первых - слишком большое число переменных, во-вторых - переменные на разных уровнях имеют неравноценное влияние на обобщенный критерий качества, что заведомо приводит к большому числу не всегда эффективных шагов поиска.
Указанные затруднения можно преодолеть, имея в виду, что проектно-конструкторские задачи допускают двухуровневое (фрагмент В на рис. 1.1) или трехуровневое (фрагмент А на рис. 1.1) представление устройства.
При двухуровневом представлении элемент (i + l)-гo уровня рассматривается как некоторое устройство (блок) с соответствующим делением на составные элементы (компоненты) i -го уровня.
При трехуровневом представлении элемент (i + 2)-гo уровня рассматривается как некоторое устройство (псевдосхема) с соответствующим его делением на блоки (элементы (i + l)-ro уровня и компоненты (элементы i-гo уровня).
Для автоматизации процесса проектирования в первую очередь необходима высокая унификация узлов проектируемой ЭВА, так как состав и последовательность задач, решаемых при конструкторском проектировании, определяются делением устройства на конструктивные единицы (блоки). Представление устройства в виде совокупности блоков разного уровня определяет формальную структурную модель конструкции ВУ, в которой каждый блок содержит блоки нижних уровней. Таким образом, конструктивное деление цифрового устройства обладает иерархией. В иерархических системах обычно пользуются понятием ранга блока.
Блок I уровня — конструктивно законченная схема, в которой невозможно выделить элементы, не нарушив целостности конструкции.
Блок II уровня — типовой элемент замены (ТЭЗ) — основная конструктивная единица, служащая для электрического объединения блоков I уровня на монтажной плате.
Блок III уровня — панель, объединяющая ТЭЗы.
Блок IV уровня — рама, на которой размещаются панели.
Блок V уровня — стойка, объединяющая несколько рам и дополнительных устройств.
Иерархическая структурная модель конструкции ВУ, заданная делением всей конструкции на блоки разного уровня, обеспечивает удобство проектирования, изготовления, эксплуатации и является необходимым условием для применения машинных методов проектирования.
Постановка и решение конструкторских задач невозможны без определения математической модели монтажного пространства для каждого уровня блоков. Монтажным пространством блока i-ro уровня называется некоторая область, ограниченная габаритами этого блока. Монтажное пространство является метрическим пространством, в котором размещаются блоки (i—1)-го уровня и осуществляется их электрическое соединение. Различают регулярные и нерегулярные монтажные пространства
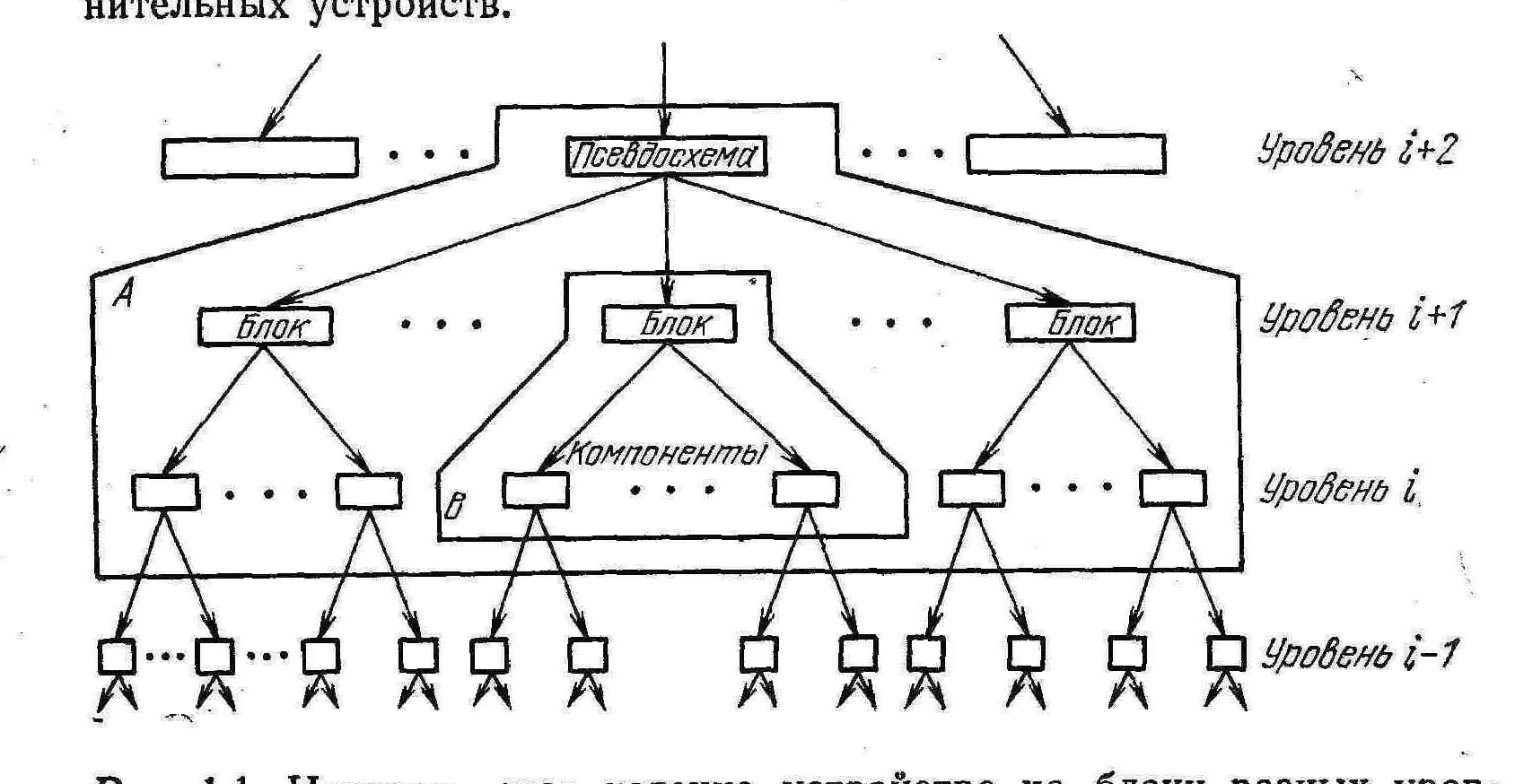
Рис 1.1 Иерархическое деление устройства на блоки разных уровней
Регулярное МКП характеризуется конечным числом заранее заданных позиций т для размещения блоков (i—1)-го уровня и числом слоев r, в которых располагаются трассы соединительных проводников. Координаты позиций при этом определяются размерами размещаемых компонентов и монтажного пространства, а также конструктивными ограничениями, задаваемыми технологией изготовления блока рассматриваемого ранга. Само монтажное пространство обычно имеет прямоугольную форму, а позиции располагаются с постоянным шагом по вертикали и по горизонтали (рис. 1.2). Регулярное монтажное пространство имеет, как правило, блоки старших рангов (5, 4, 3 и 2).

Рис. 1.2 Примеры монтажных пространств: а — плата с элементами; б — панель с выходами разъемов.
Блоки первого ранга (иногда второго) реализуются обычно в нерегулярных монтажных пространствах, в которых нельзя заранее определить координаты позиций, так как размещаемые компоненты имеют различные размеры и форму. Типичным нерегулярным пространством является полупроводниковый кристалл или подложка интегральной схемы (ИС).
Регулярное монтажное пространство может быть представлено в виде неориентированного взвешенного графа Gm, в котором каждой вершине х{ (i=l, 2, ., N) соответствует одна позиция монтажного пространства.
Вес ребер графа определяется в соответствии с выбираемой метрикой монтажного пространства
dij=(xi-yik+yi-yjk)s
где dij— расстояние между позициями i и j; (xi, yi) и ( xj, , yj) — соответственно координаты позиций i и j в монтажном пространстве; а k{1; 2), s{0,5; 1}. Так, при k=2, s=0,5 расстояние между позициями определяется в евклидовом пространстве, т. е. расстояние равно длине прямолинейного отрезка, соединяющего эти две позиции (Рис. 1.3). Такая метрика обычно используется при проводном соединении монтажного пространства. Если k=1, s=l, то расстояние определяется на ортогональной евклидовой решетке, т. е. расстояние равно суммарной длине двух ортогональных отрезков, соединяющих рассматриваемые позиции. Эта метрика обычно используется при печатном монтаже с ортогональной структурой.

Рис. 1.3. Фрагмент
графа
Отметим, что все сказанное относительно метрики регулярного монтажного пространства распространяется и на метрику нерегулярного пространства. Однако в НМП нельзя заранее определить координаты установочных позиций компонентов, т.к. последние имеют неодинаковые геометрические размеры. В этом случае ребра трасс могут проходить по любому ребру графа трасс.
При электрическом соединении компонентов в монтажном пространстве различают соединения, построенные на регулярных (трассы печатных схем, металлизированные и диффузионные соединения интегральных схем, жгутовые проводные соединения) и нерегулярных (проводные соединения, некоторые виды печатных трасе) структурах.
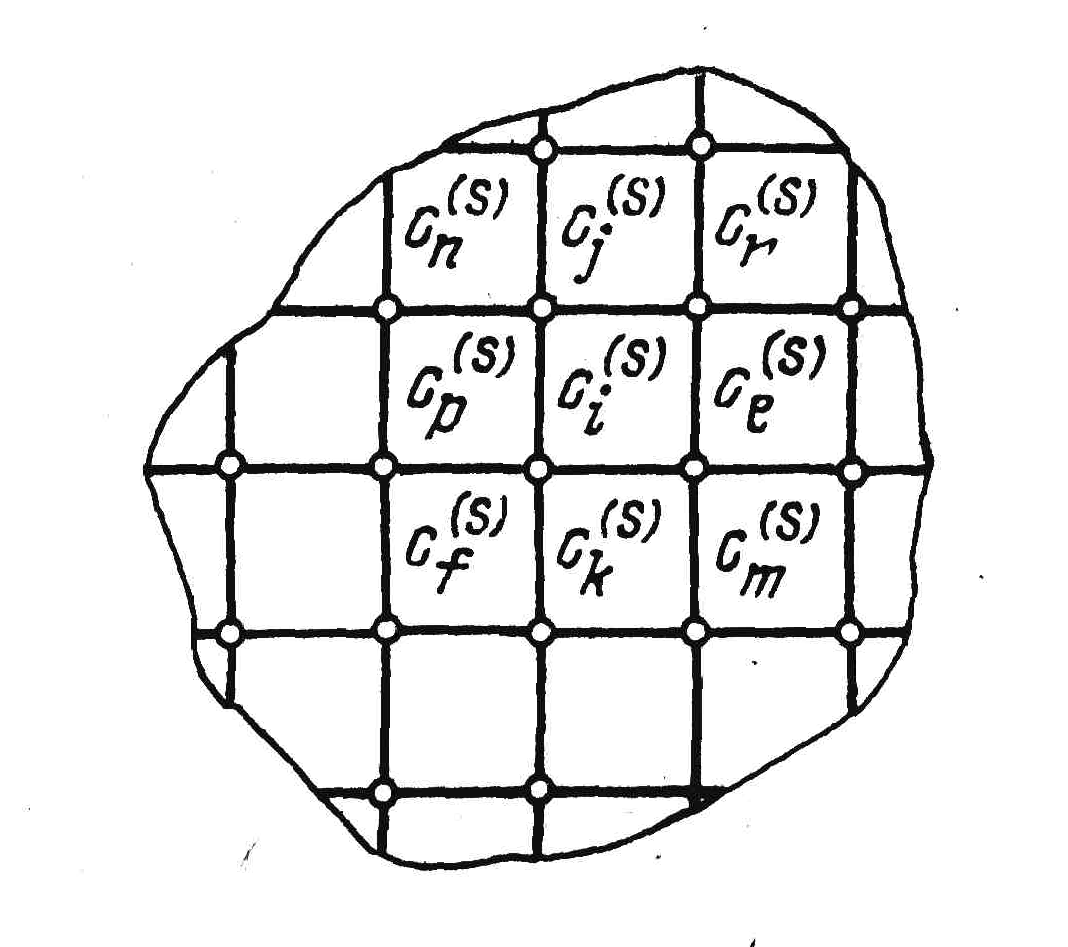
Для
построения соединений на регулярных
структурах
плоскость монтажного пространства,
предназначенную для осуществления
соединений, разбивают на ряд квадратов
равной величины, размеры которых
определяются технологией изготовления
монтажа (рис. 1.4,а). Каждому квадрату
ставится в соответствие одна вершина
графа трасс G=(C,
L).
Вершины ciС
и cjC
соединяются ребром, если соответствующие
им квадраты являются соседними, т. е.
если при реализации
соединений допускается прокладка трассы
из
квадрата ci
в cj.
Для
ортогонального монтажа соседними
квадрату
ci
(рис.
1.4,а) являются квадраты (cj
,
се
,
сk
,
cр
}.
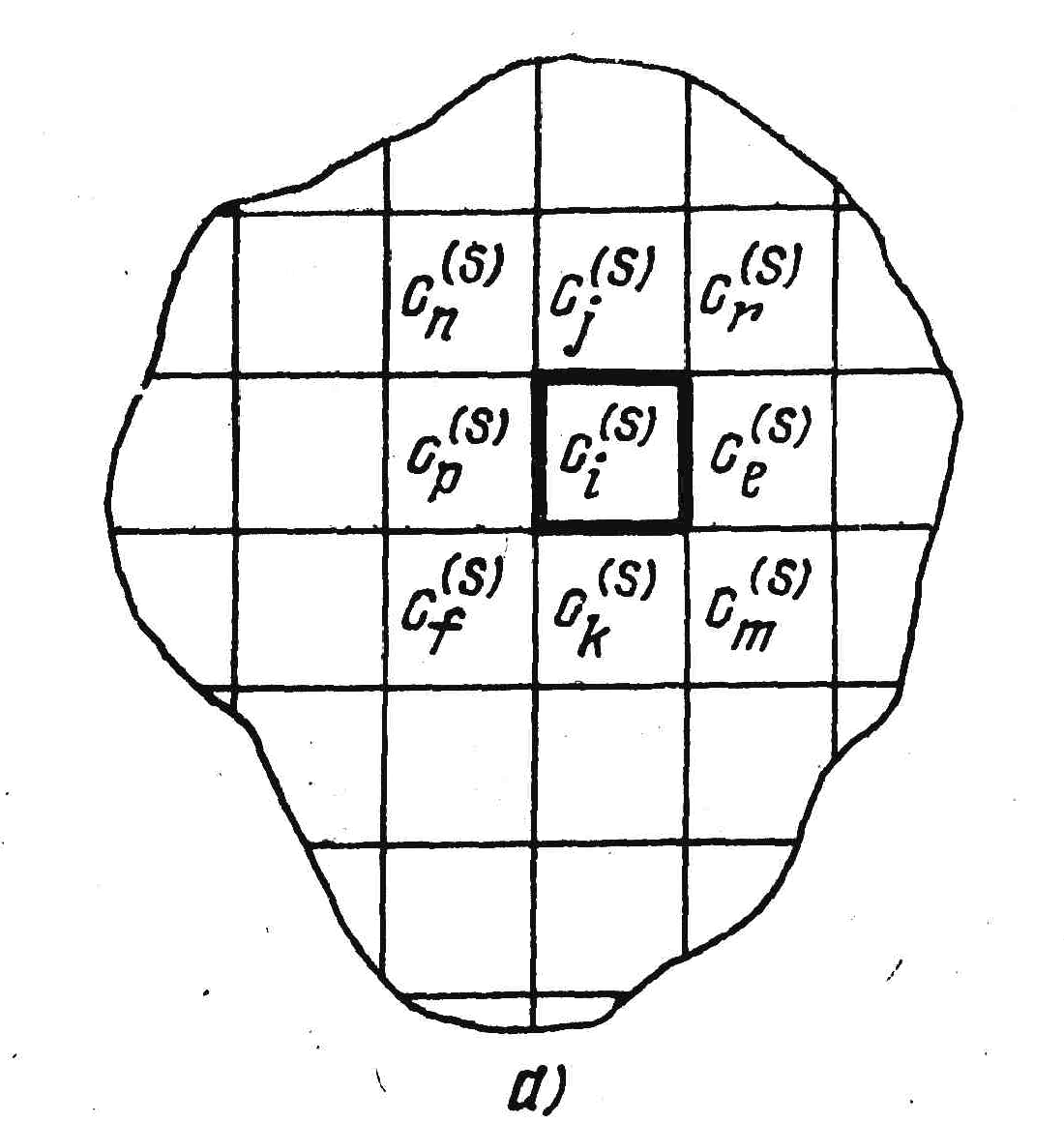
При
этом граф трасс имеет структуру решетки
(рис. 1.4,б). Если допускается прокладка
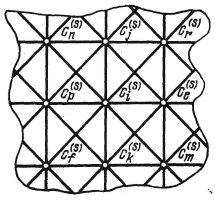
трасс под углом 45о
, то соседними по квадрату сi
являются квадраты ![]() .Соответствующий
граф трасс для этого случая показан на
рис. 1.5. Соединительные трассы могут
проходить только по ребрам (i
и
j)
L
графа трасс.
.Соответствующий
граф трасс для этого случая показан на
рис. 1.5. Соединительные трассы могут
проходить только по ребрам (i
и
j)
L
графа трасс.
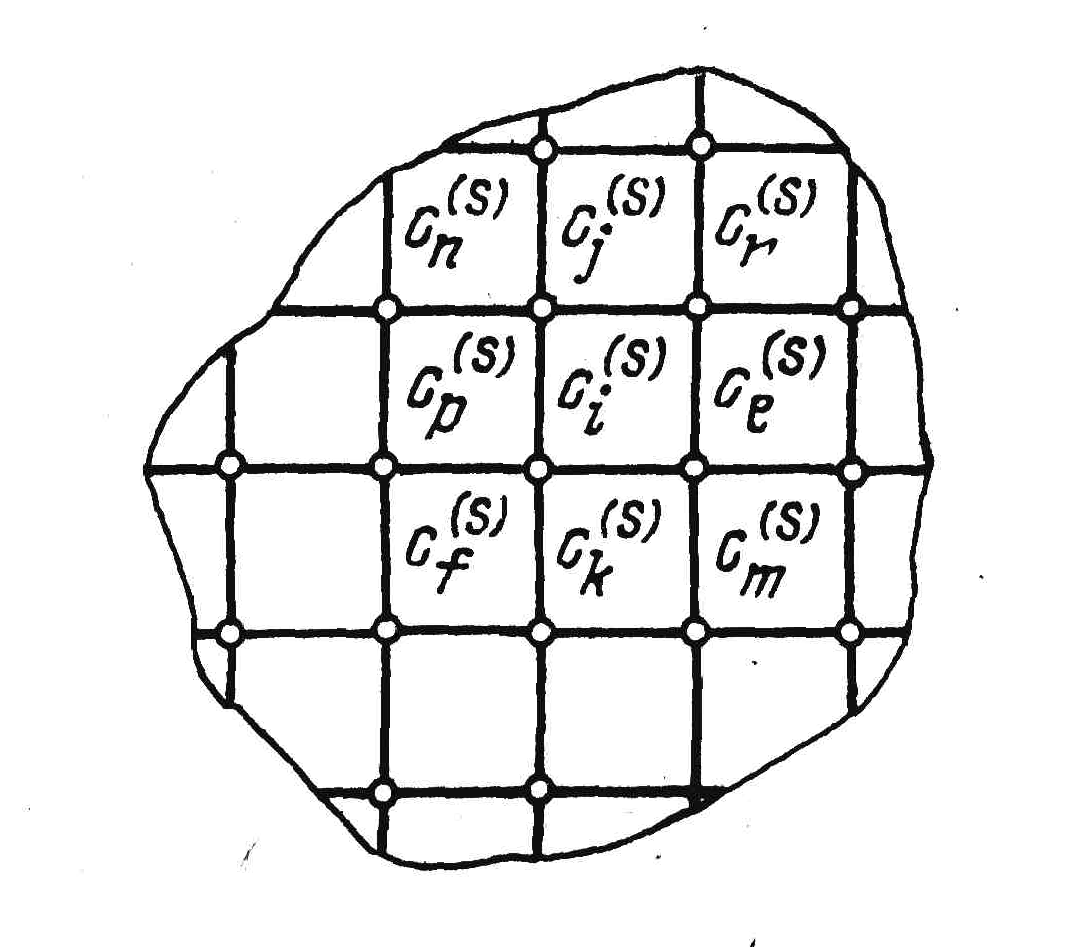

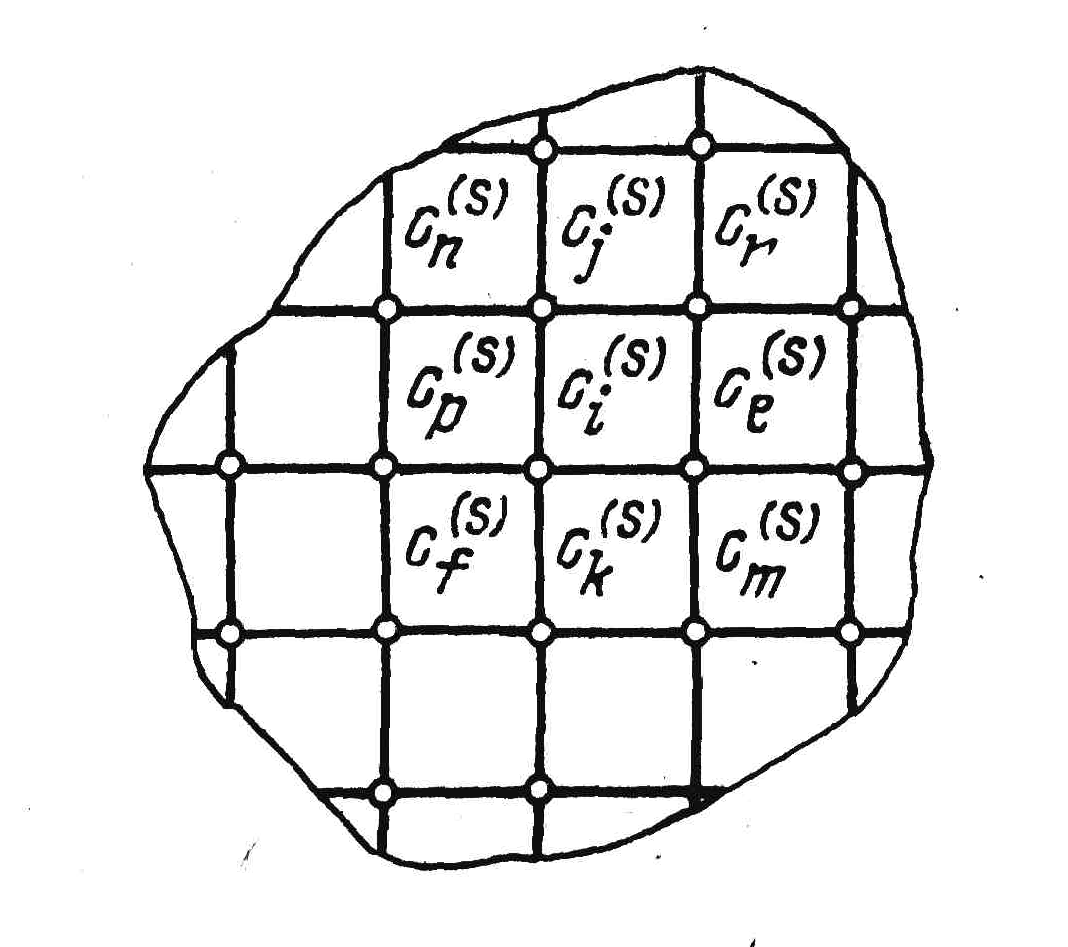
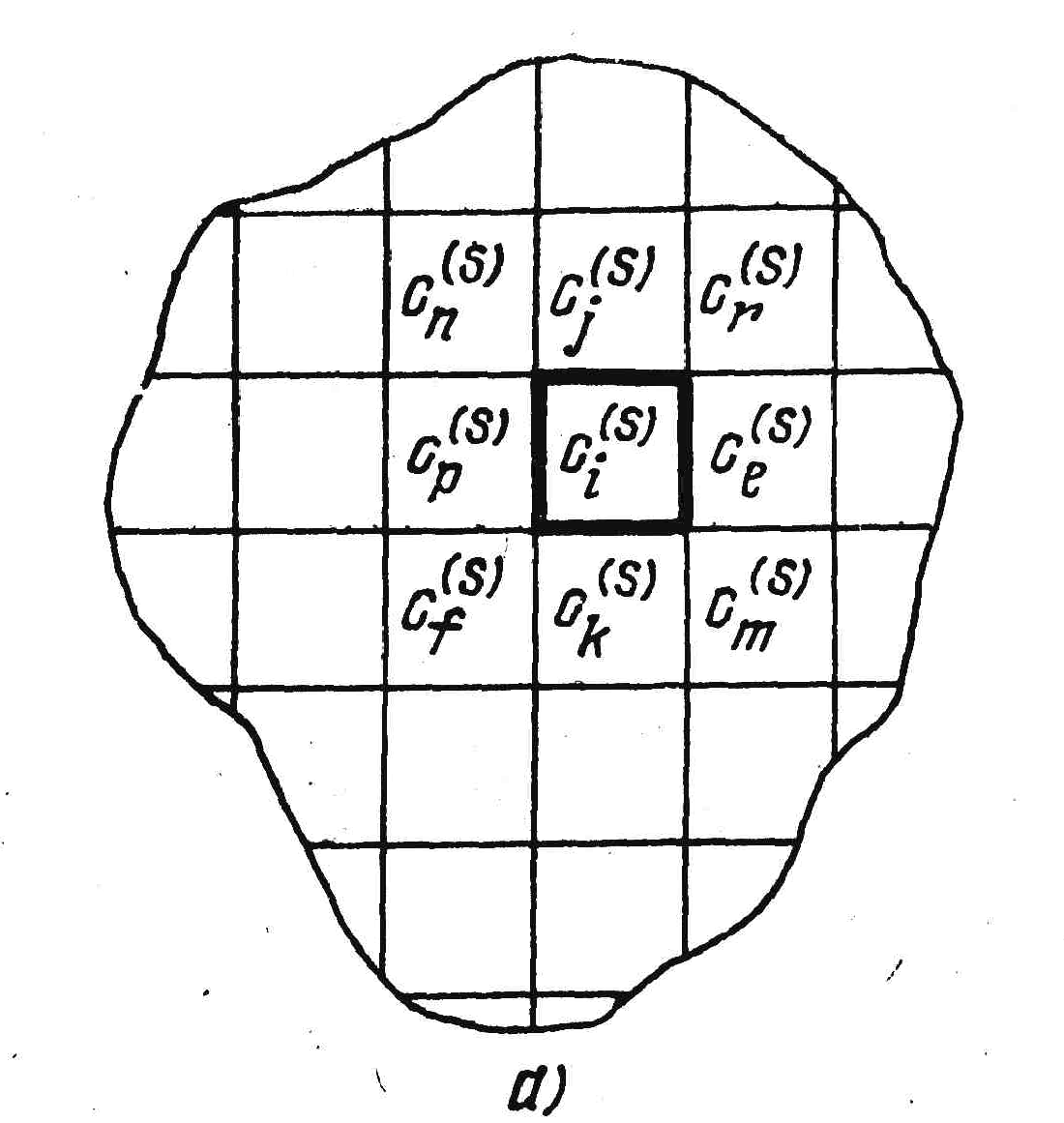
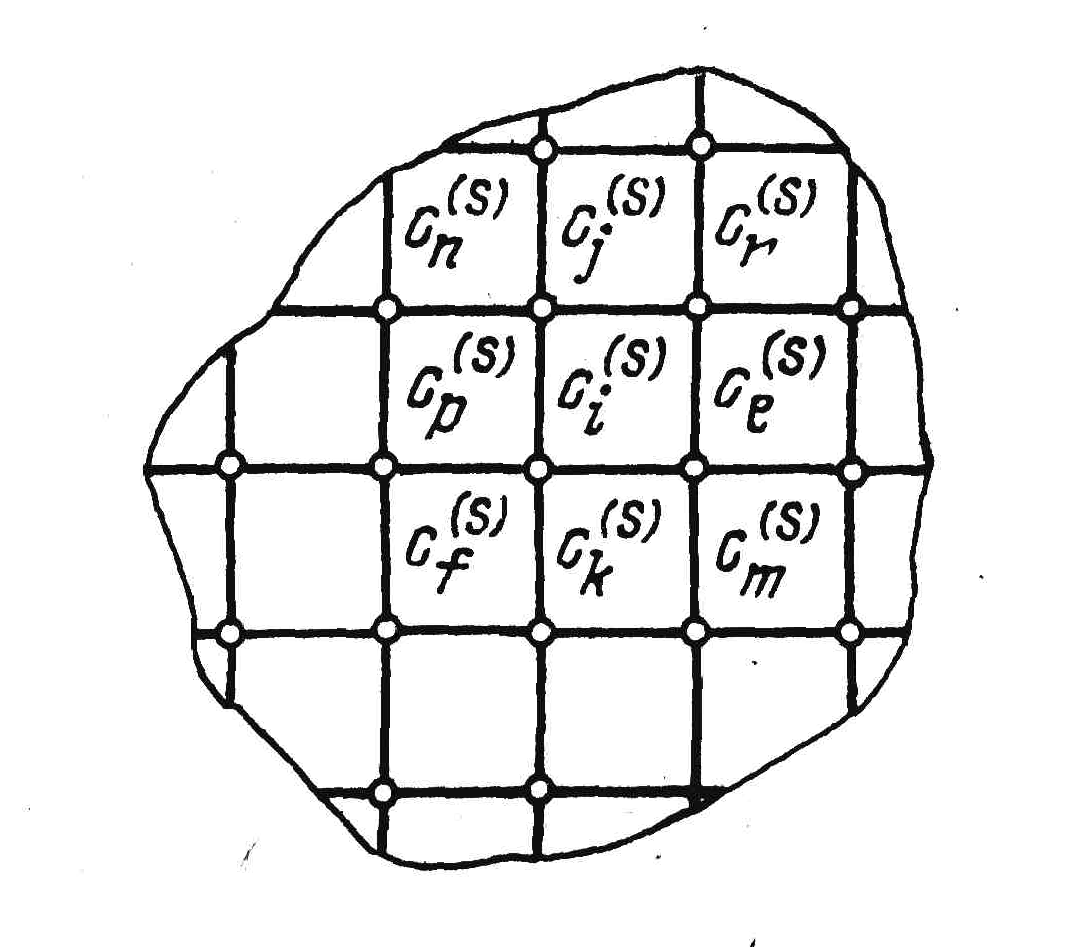


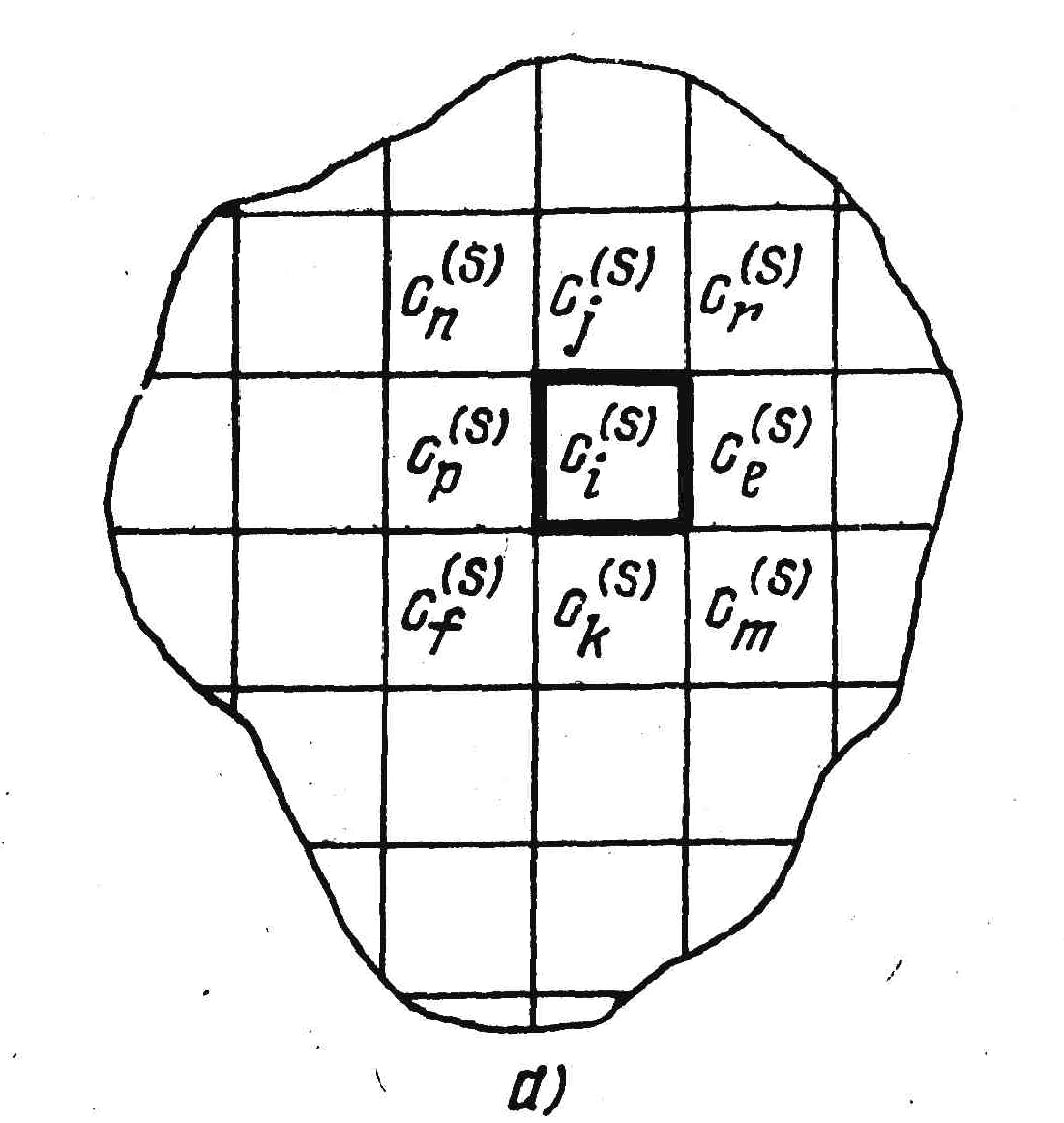
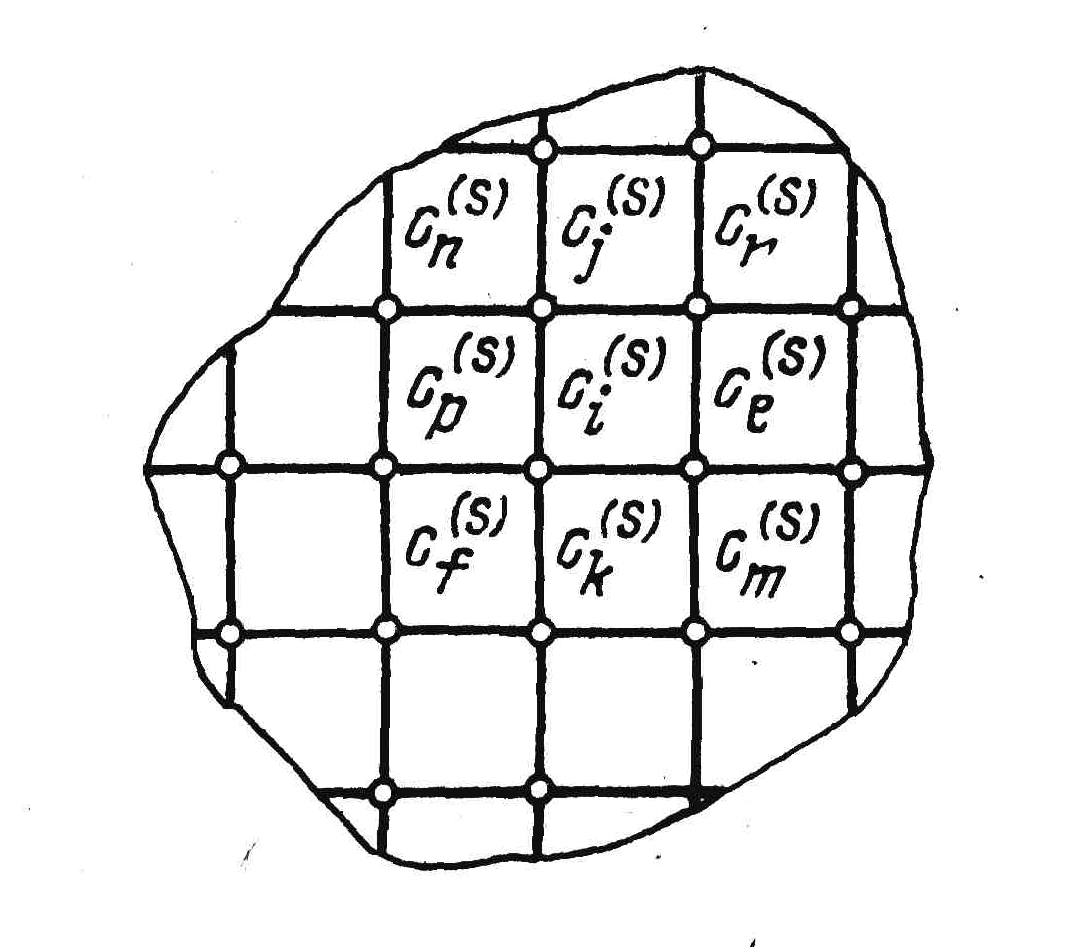
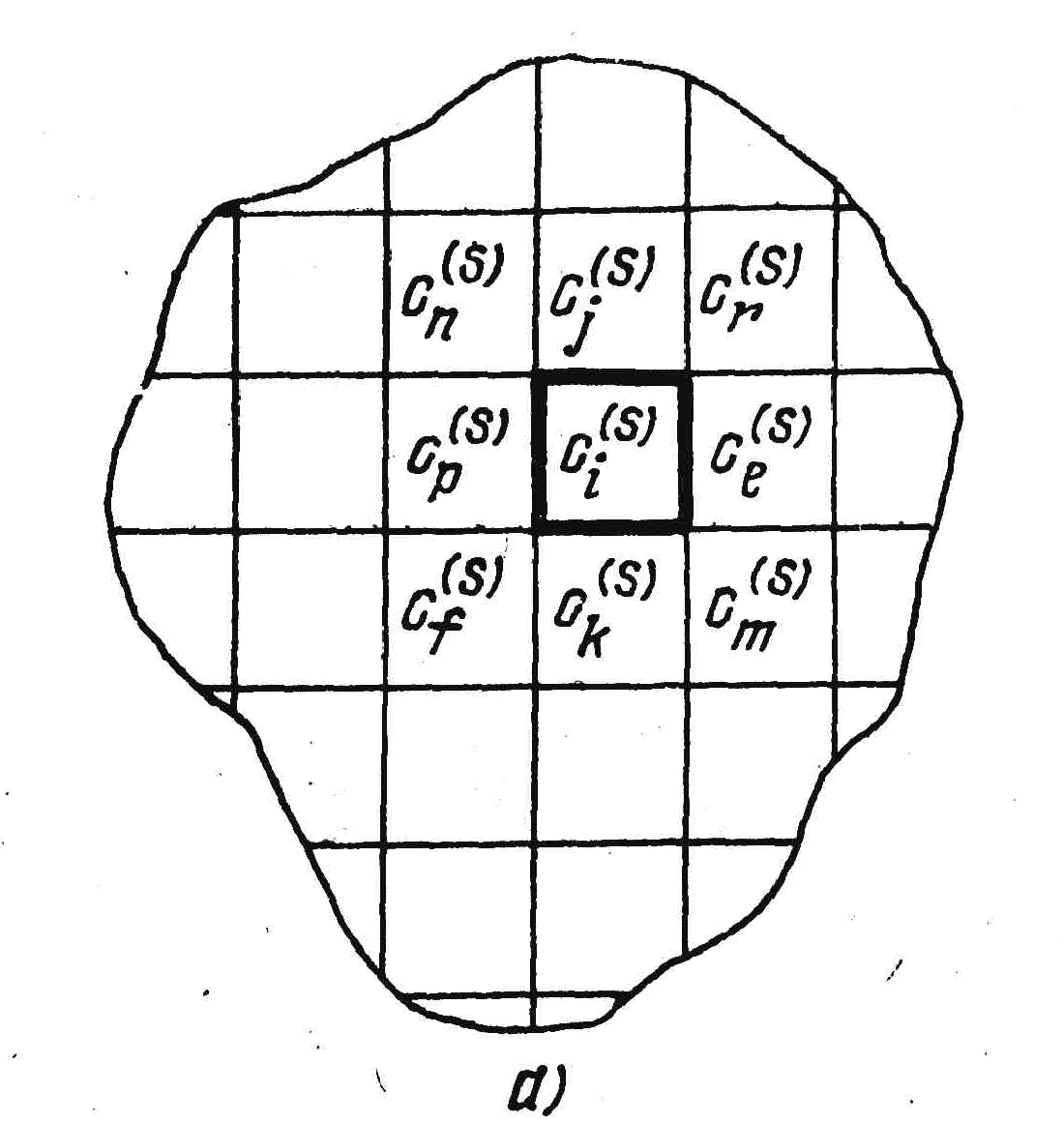
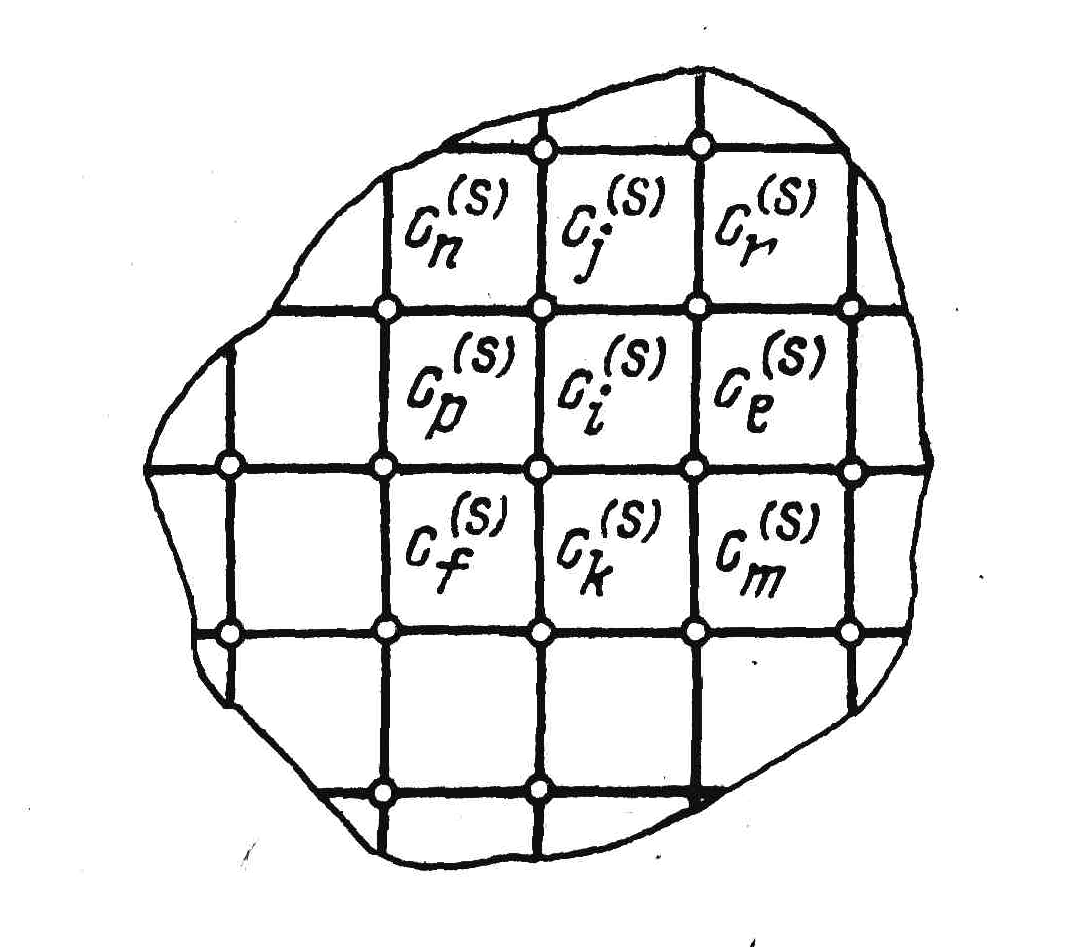
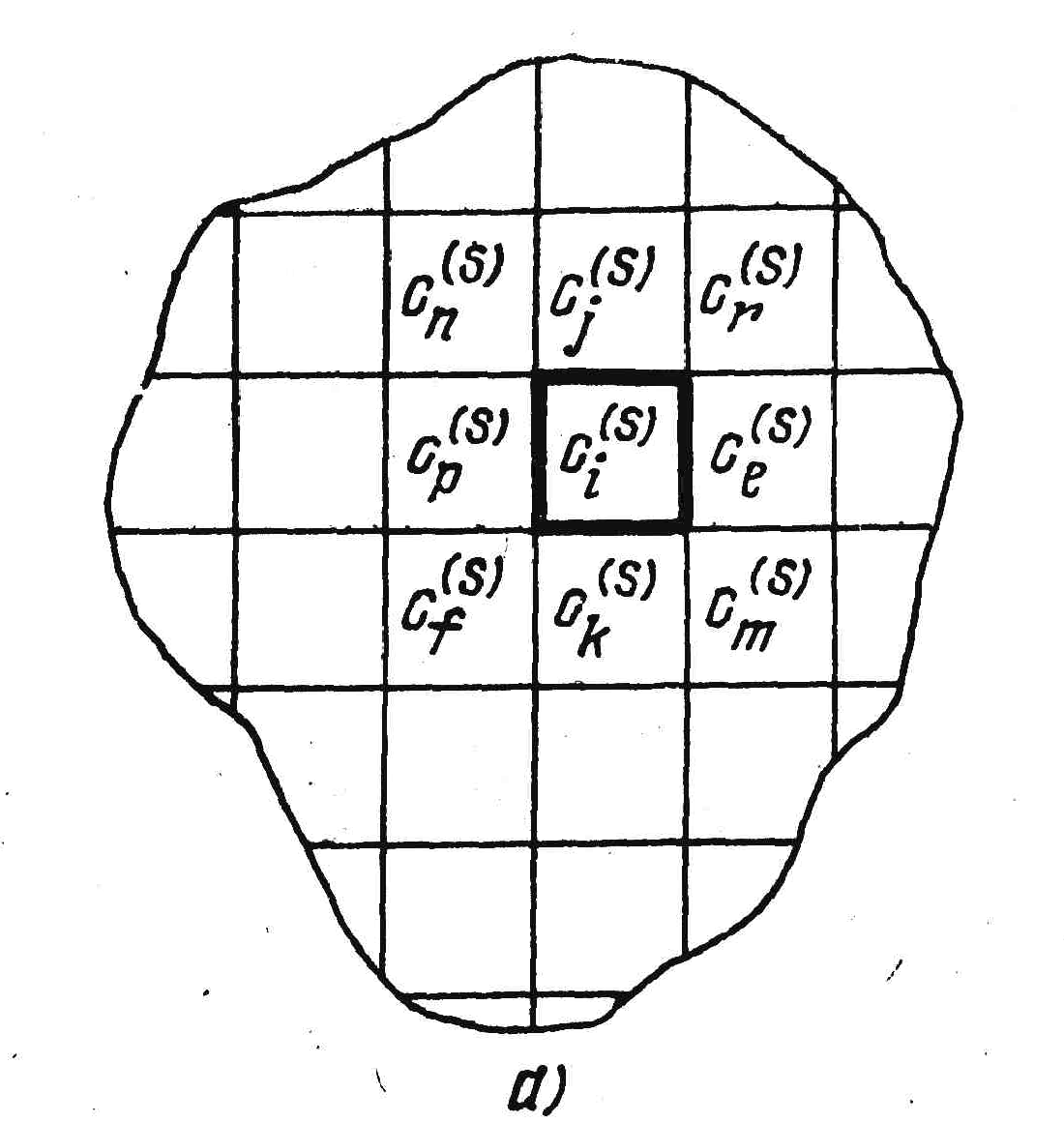
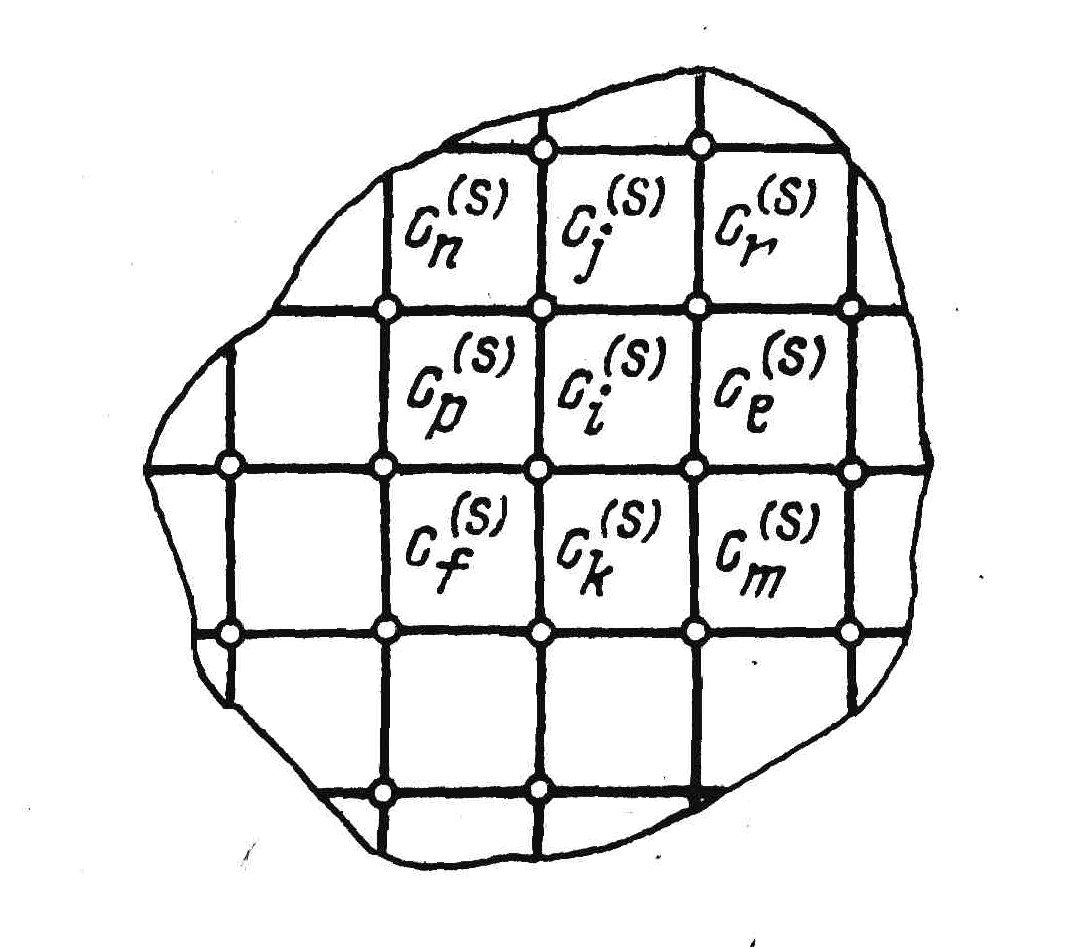
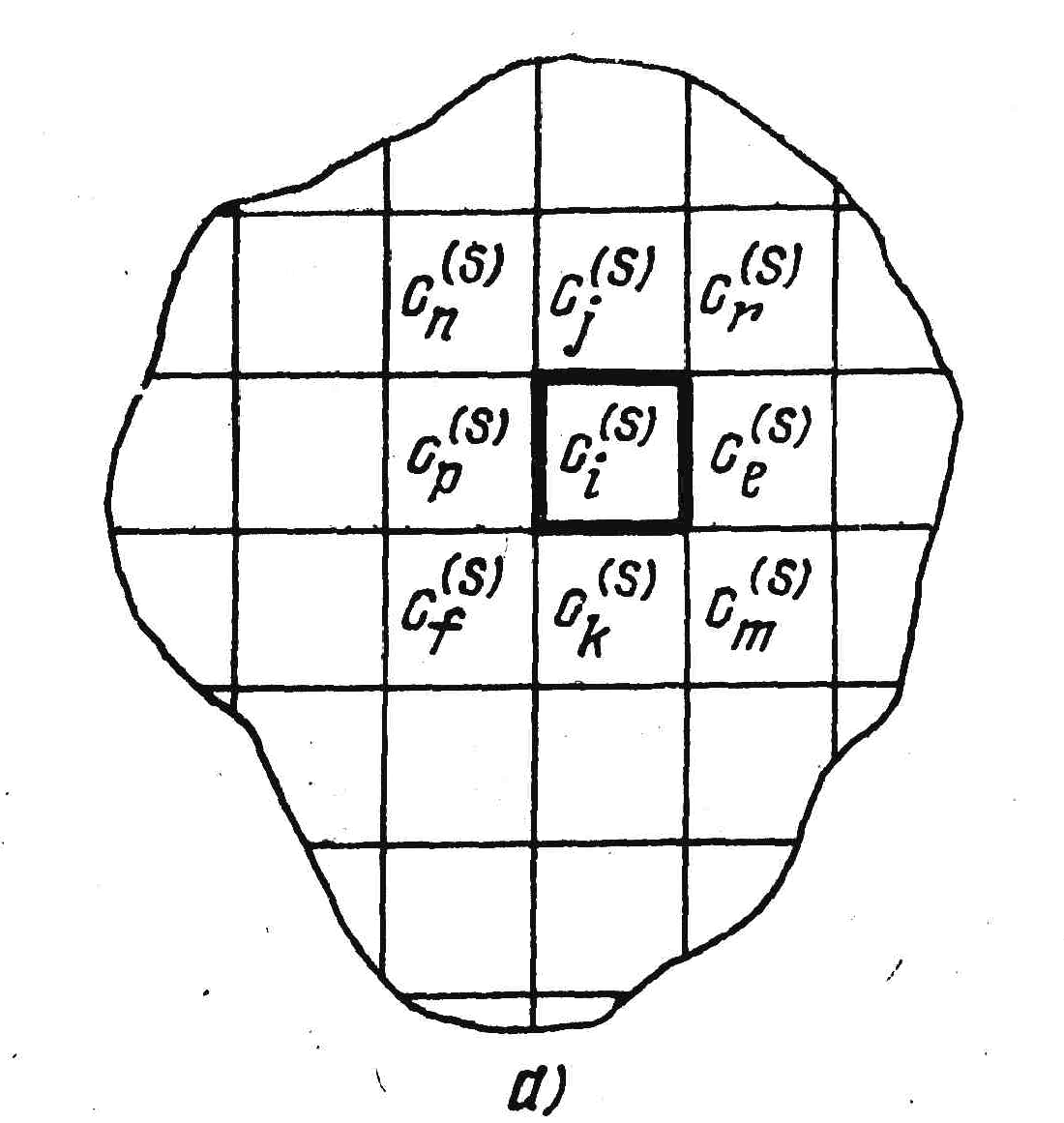
а) б)
Рис. 1.4. Дискретизация монтажного пространства.
Рис.
1.5. Фрагмент графа трасс. Рис.
1.6. Фрагмент графа трасс многослойной
структуры

Напомним, что электрической цепью называется часть принципиальной схемы, у которой все точки имеют одинаковый потенциал. При жгутовом монтаже ограничивается число проводов, которое может быть проложено вдоль одного ребра графа G и т. д.
В случае многослойного монтажа G образуется объединением графов трасс отдельных слоев (рис. 1.6) путем введения дополнительных ребер переходов между слоями в соответствии с технологией изготовления монтажа.
При построении соединений на нерегулярных структурах соединительные проводники могут проходить по любому ребру полного графа (рис. 1.3), вершинам которого соответствуют контакты элементов. Как правило, при этом ограничивается число проводников, инцидентных одной вершине.
Задачи конструкторского проектирования ВС принадлежат к классу комбинаторных оптимизационных задач. Применяемые методы решения существенно зависят от выбираемой формальной математической модели схем электронных устройств. К тому же различные модели с различной точностью описывают одни и те же параметры устройства при решении каждой конкретной задачи конструкторского проектирования. Поэтому на различных этапах проектирования ВС, в зависимости от конкретных оптимизируемых критериев, могут быть использованы разные модели.
При сравнении моделей учитывают следующие показатели;
1. Степень применимости для решения конкретной задачи конструирования.
2. Точность описания основных параметров устройства.
3. Сложность работы с моделью (сложность алгоритмов обработки).
4. Сложность определения параметров модели (сложность перехода от схемы к модели).
5. Сложность описания модели.
6. Степень разработанности математического аппарата для данной модели.
7. Информационную сложность модели (возможность перехода от описания одной модели к более простой).
