Размещение компонентов в регулярном монтажном пространстве
Регулярное монтажное пространство представляет собой прямоугольную область с регулярно расположенными позициями.
Пусть требуется разместить компоненты X1, X2,…..XN на множестве К позиций монтажного пространства.
Введем псевдобулевы переменные
{
1, если xi размещен в позицию l.
il =
0, если компонент xi не назначается в позицию l
Модель 1.
Задана матрица R = || rij ||NxN
Тогда задача размещения при использовании модели 1 может быть сформулирована в следующем виде.
Минимизировать
L
=
rij
*il*js
*dls
Где rij – элемент матрицы связей,
dls – расстояние между посадочными местами l и s,
при ограничениях:
il
= 1 –
гарантирует,
что любой модуль будет размещен только
один раз,
il
= 1 –
гарантирует
что каждая позиция будет используется
только один раз.
Модель 2
Задана матрица = ||||if и k = N (k –число установочных позиций, N – число модулей).
Введем целочисленные переменные zi и yj, i=l,N, которые соответственно определяют номера вертикального и горизонтального рядов, на пересечении которых находится модуль Xi.
Тогда задача размещения может быть представлена в виде задачи линейного целочисленного программирования.
Минимизировать полупериметр зоны реализации L цепи tf
L
=
(zfmax
– zfmin)
+ (yfmax
– yfmin)
при ограничениях
xi X(tf) zfmax zi; zfmin < zj
yfmax yi; yfmin < yj, а также должно соблюдаться условие
zi ≤ A и yi ≤ B, где A и B – размеры монтажного поля.
(zi yi) и (zjyi) – координаты модулей xi и xj соответственно.
Размещение компонентов в нерегулярном монтажном пространстве
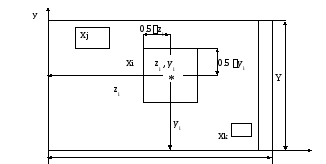
В отличие от предыдущей задачи геометрические размеры размещаемых компонентов в данном случае могут быть различными. Будем полагать, что монтажное пространство имеет прямоугольную форму размера ZxY, а каждый размещаемый компонент аппроксимирован прямоугольником с размерами zi х yi соответственно.
Введем переменные zi и yi i=l,N, которые определяют координаты размещения центра модуля хi. Тогда для модели 1 задача размещения может быть сформулирована как задача линейного программирования.
Минимизировать
L
=
rij*(zij
+ yij)
, где
zij = |zi – zj|, yij = |yi – yj|
п
{
{
{
{
{
{
{
{
{
{
{
{
{
{
{
{
zij > (1 - ij) * (zi + zj)/2 1, если zi = zj
, где ij = (*)
yij > ij*(yi - yj)/2 0
zi 0.5zi Z – zi 0.5zi; yi 0.5yi Y - yi 0.5yi (**)
Z
Условия (*) гарантируют, что модули не пересекаются (не накладываются друг на друга) в монтажном пространстве.
Условия (**) гарантируют, что модули находятся в пределах габаритов монтажного пространства.