Пример алгоритма типизации.

Задана коммутационная схема

П1.Выделение в исходной схеме равноинвариантных вершин (тип модуля и количество выводов). Таких типов модулей – два.

Т и п 1 Т и п 2

К Типу 1 относятся исходные модули {2, 3, 6, 7} – Группа 1.

К Типу 2 относятся исходные модули {1, 4, 5, 8} – Группа 2.

П2. Построение матриц связей модулей, входящих в разные группы разбиения, и нахождение максимального количества блоков, состоящих из двух вершин (модулей).

2 3 6 7

12 1 0 1

4 1 1 1 2

R=||r_ij|| = 5 0 1 2 2

8 1 1 1 1

П3. В разных строках и столбцах матрицы выбираем максимальные элементы матрицы, и формируем из соответствующих исходных модулей новую пару укрупненных (по два) модулей.

П4. Получим два одинаковых модуля М1, состоящих из пар исходных модулей M1' = {1 2} и M1" = {5 6}, и два одинаковых модуля М2, состоящих из пар исходных модулей M2' = {3 8} и M2" = {4 7}.

Нарисуем эти два новых типа модулей:

3 2 4 3

7 (6) (7) 5

6

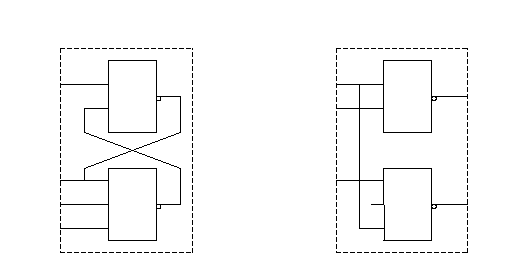
Модуль М1 Модуль М2

1 1 3 8

(5) (4)

1 10

3 2 4 3

7 (6) (7) 5

6

П5. "Перерисуем" исходную схему в виде совокупности модулей М1 и М2.

Переход к П2.

Строим матрицу связей для новых модулей М1 и М2.

M1' M1"

{1 - 2} {5 – 6}

R' = M2' {3 – 8} 2 2

M2" {4 – 7} 2 2

П3, П4. Объединяем модули в пары – M3(M1' M2') и M4(M1" M2").

П5. Формируем новый вид схемы.

M3 1 M4

{1-2-3-8} 4 {4-5-6-7}

5

6

7

10

Результат: получен один стандартный модуль М  М3 и М4.

Покрытие функциональных схем модулями заданного библиотечного набора

Одной из первых задач, решаемых на этапе конструкторского проектирования РЭА, является задача преобразования функциональной схемы в электрическую (покрытие функциональной схемы модулями заданного набора). Т. е., в схему соединения выводов конструктивных элементов (резисторов, конденсаторов, транзисторов, интегральных схем и т. д.). В связи с большим многообразием элементов, применяемых в электрических схемах, наряду с задачей покрытия часто возникает необходимость:

- определения оптимального набора этих элементов для каждого конкретного класса схем,

- минимизации числа типов элементов набора в проектируемом устройстве.

Вопросы алгоритмизации подобных задач начали разрабатываться недавно, тем не менее, общую схему их решения наметить можно.

Математическая формулировка. Исходными данными для решения задачи покрытия являются: функциональная схема устройства и схемы типовых конструктивных элементов используемого набора модулей. Необходимо найти такое распределение логических функций покрываемой схемы по отдельным конструктивным элементам, при котором достигается экстремум целевой функции. Известные в литературе алгоритмы покрытия оптимизируют в основном следующие показатели качества:

1) суммарную стоимость модулей, покрывающих схему;

2) общее число модулей, необходимое для реализации схемы;

3) число типов используемых модулей;

4) число межмодульных соединений и т. д.

Ограничениями обычно являются требования на совместную или раздельную компоновку в едином конструктивном модуле элементов функциональной схемы, связанные с обеспечением нормального теплового режима, помехозащищенности и простоты диагностики.

Рассмотрим наиболее распространенный вариант задачи, в которой критерием качества является суммарная "стоимость" модулей. Воспользуемся для ее решения методами целочисленного линейного программирования.

Определим некоторую матрицу

Н = || h_ij ||_{k x l}

общий элемент которой h_ij соответствует числу логических функций i-ro типа в j-ом модуле, где k — общее число различных логических функций, реализуемых модулями заданного набора; l — общее число типов модулей в наборе.

Пусть полная функциональная схема содержит а₁, а₂, •a_i,• a_m (m ≤ k) единиц различных логических функций, а с_j — "стоимость" j-го конструктивного модуля (j =1,2, ..., l). Если ввести целочисленные переменные n_j (j = 1, 2, ..., l), определяющие число модулей j-го типа, которые необходимы для покрытия схемы, то задача сведется к минимизации функции

F (X) = c_j * n_j  min

при ограничениях h_{ij *} n_j  a_i,

i = 1, 2, ..., k (т.е. число логических функций любого i-гo типа, входящих во все покрывающие модули, должно быть не меньше общего числа элементов соответствующего типа в реализуемой схеме);

n_j  0, j = 1,2,...,l;

h_ij  0,

n_j — целое число для всех j (любой модуль используется только полностью, независимо от числа задействованных в нем контактов).