
- •Компьютерные технологии проектирования вычислительных устройств
- •Структура сапр
- •1. Математические модели конструкций и схем ву
- •Модель компонента
- •Модели электрических схем
- •Компьютерные технологии проектирования печатных плат в среде p-cad Создание символов компонентов
- •Конструкторско-технологические параметры печатных плат
- •Отверстия печатных плат
- •Стеки контактных площадок (Pad Stacks) и переходных отверстий (Via Stacks).
- •Создание на пп посадочных мест компонентов.
- •Создание схемы электрической принципиальной
- •2). Размещение модулей на мкп
- •Алгоритмы и модели компоновки ву
- •Критерии оптимизации при разрезании электрической схемы
- •1 , Если tf t(xj)
- •Итерационный алгоритм разбиения гиперграфа
- •Пример алгоритма типизации.
- •Покрытие функциональных схем модулями заданного библиотечного набора
- •Задача размещения модулей.
- •Размещение компонентов в регулярном монтажном пространстве
- •Размещение компонентов в нерегулярном монтажном пространстве
- •Алгоритм последовательного размещения
- •Метод силовых функций (непрерывно – дискретный алгоритм размещения)
- •Задача "перераспределения" выводов модуля
- •Подсчет изменения суммарной длины связей в итерационных алгоритмах
- •Трассировка электрических соединений
- •Математическая формулировка задачи трассировки электрических соединений.
- •Алгоритмы трассировки
- •Эвристический алгоритм трассировки. Двухлучевой алгоритм трассировки
Модель компонента
При оптимизации электрических соединений необходимо учитывать конструктивно-технологические особенности компонентов и МП:
Порядок расположения выводов;
Возможность прохода соединений между выводами;
Эквивалентность некоторых выводов или групп выводов и т.д.
Каждый компонент схемы может быть представлен в виде многополюсника, имеющего некоторое подмножество выводов {cgi}. В общем случае выводы модуля не являются инвариантными, т.к. каждый из выводов соответствует определенному входу (выходу) электрической схемы самого модуля.



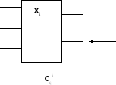



 Для
реализации задачи трассировки не-
Для
реализации задачи трассировки не-
обходимо задать информацию о взаим-
ном расположении выводов модуля и
tf задать бинарные соотношения между
тремя множествами:
- множеством модулей (компонентов) X={xi}, i=1,N, |X|=N;
- множеством выводов модулей С={cgi}, g=1,ni, | cgi |=ni;
-множеством электрических цепей T={tf}, f=1,M, |T|=M.
Модели электрических схем
Матричные модели электрических схем
Матрица цепей Т = XC(T) размерностью N x g i max. Элементом матрицы является номер электрической цепи tf, инцидентный j-тому контакту i-того модуля, g i max – максимальное число контактов i-того модуля.
Внимание!!! Недостаток матрицы (N x g i max).
Матрица контактов C = XT(C) размерностью M x N. Элементом матрицы является номер вывода i-того модуля, инцидентный цепи tf.
Матрица модулей (компонентов) X = TC(X) размерностью M x gmax. Элементом матрицы является имя модуля, у которого контакт cji инцидентен цепи tf.
Т.к. на практике M>N и N>>g, то размерность матрицы Т меньше, чем размерность матриц С и Х, поэтому более часто применяется матрица Т.
Если среднее число подключенных выводов модулей в схеме ССР < 0,5(gmax– 1), то информацию о схеме целесообразно задавать в виде списков.
Экстремальные задачи конструкторского проектирования удобно формулируются в терминах теории графов. При решении этих задач с помощью ЭВМ широкое распространение получили следующие математические модели, представляющие схемы электронных устройств, описанные ниже в порядке повышения их информационной сложности.
Графовые модели электрических схем
Модель 1 (Мультиграф схемы)
Компоненты схемы представляются вершинами X={x1, x2, ..., xN}, а внешние контактные площадки (ВКП) электрических цепей схемы — вершинами К={K1, K2, • • •, Kn} неориентированного взвешенного графа G(Z, V), где Z=XK.
В мультиграфе G каждая электрическая цепь tf представлена своим полным подграфом (Рис. а), включающим все вершины, инцидентные данной цепи, а вес ребра rij зависит от числа связей между элементами i и j схемы. Такое представление схемы, в силу избыточности данных, может привести к искажениям при решении конструкторских задач.
X


 1
X5
X1
X5
1
X5
X1
X5

X6 K2 X6 K2
Рис. а) Рис. б)
Полный подграф Одно из возможных
для цепи t2 деревьев цепи t2
Согласно теореме Кэли число возможных деревьев на полном графе определяется по формуле D=NN-2, где N – число вершин графа. В определенной мере этот недостаток может быть скомпенсирован, если при определении веса ребер (коэффициент связей) графа G учитывать различие полных графов и графов реальных электрических цепей, представляющих собой дерево.
На Рис. б) представлено одно из 16 возможных деревьев для цепи t2.
Для представленной схемы матрица связей R={rij}NxN имеет след. вид:
Характеристики Модели 1:
1. Модель может быть использована при решении задачи компоновки, однако минимизируемый критерий (число ребер между блоками разбиения) при этом не совпадает с конструктивным критерием (числом электрических связей между блоками). В то же время эти критерии имеют сильную корреляционную связь и минимизация, одного, как правило, приводит к снижению другого. Модель 1 можно с успехом применять при решении задачи размещения. Это связано с тем, что пока не существует точного конструктивного критерия решения этой задачи и на практике применяются эвристические показатели качества размещения. Причем наиболее простые из них введены в предположении использования модели 1. Для решения задачи трассировки и исследования планарности модель применяться не может.
2. На основании модели, как уже отмечалось, нельзя точно определить основные параметры устройства.
3. Модель представляет собой граф, который описывается матрицей ||rij||. Поэтому все алгоритмы обработки модели достаточно просты.
4. Переход от схемы к модели 1 не представляет сложности и состоит из определения коэффициентов связи и формирования матрицы ||rij||.
б. Модель описывается с помощью симметричной матрицы ||rij|| размера NхN. Недостатком такого описания является значительный объем машинной памяти, который необходим для хранения матрицы ||rij||.
6. Одним из факторов, способствующих широкому применению модели, является хорошо разработанный аппарат теории графов и матриц.
7. Модель, является наиболее простой и по информационной сложности. Поэтому от описания этой модели нельзя перейти к описанию других моделей.
Модель 2 (Гиперграф схемы)
Гиперграф G(Z T) схемы представляет собой множество вершин Z=XK и множество ребер T={t1 t2 t3, …, tМ}, где М – число электрических цепей (при сквозной нумерации). Каждому ребру гиперграфа однозначно соответствует некоторая электрическая цепь.
С другой стороны, каждое ребро гиперграфа представляет собой некоторое подмножество вершин Z(tf), инцидентных цепи tf.
Гиперграф, а, следовательно, и электрическая схема, может быть представлен в виде списков, с помощью матрицы инциденций и в виде графа Кёнига (двудольный граф).
Списки гиперграфа.
а) Список T(zi) – список электрических цепей, инцидентных вершине zi:
Пример списка T(X1) = (t2 t3 t4), T(X2) = (t1 t4 t3), T(X5) = (t2 t3 t7).
б) Список Z(tf) – список модулей, инцидентных цепи tf.
Пример списка Z(t2) = (K2 X1 X5 X6), Z(t3) = (X1 X2 X5).
Матрица инциденций гиперграфа.
Элементом матрицы является псевдобулева переменная
{
δij = 1, если zi Z(tf) или tf T(zi)
0
Пример матрицы инциденций см. ниже.
Граф Кёнига для гиперграфа.
Гиперграф м.б. представлен в виде графа Кёнига G(Z' V') с множеством вершин Z'=ZT и множеством ребер V'= TX таких, что вершины zi и tf смежны тогда и только тогда, когда вершина zi смежна ребру (цепи) tf (двудольный граф).
Пример графа Кёнига представлен ниже.
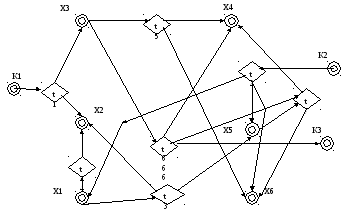
Граф Кёнига
t1 t2 t3 t4 t5 t6 t7



 X1
1 1 1
X1
1 1 1
X2 1 1 1
X3 1 1 1
X4 1 1 1
||δif|| = X5 1 1 1
X6 1 1 1
K1 1
K2 1
K3 1
Матрица инциденций
Характеристики модели 2
1. Модель можно использовать для решения задач компоновки, размещения и (при соответствующей модификации) трассировки.
2. На основании модели можно точно определить все основные конструктивные параметры устройства.
3. Модель представляет собой гиперграф, и все алгоритмы решения конструкторских задач с ее использованием достаточно сложные.
4. Переход от схемы к модели заключается в установлении взаимнооднозначного соответствия между электрическими цепями и ребрами гиперграфа, что не вызывает сложности.
5. Модель описывается одним из следующих способов:
или в виде списков Z(tf), T(zi) или с помощью матрицы инциденций ||δ if ||.
Описания в виде списков более экономичны в смысле занимаемого объема памяти по сравнению с матрицей. Однако применение матрицы значительно сокращает время работы алгоритмов обработки данных. Поэтому в ряде случаев может быть оправдано использование матричной модели гиперграфа, особенно, если при ее кодировании применяется уплотненное хранение информации ||δ||if
Таким образом, исходную информацию о гиперграфе целесообразно представлять и вводить в ЭВМ в виде списков (объединение подмножеств). При этом резко уменьшается вероятность возникновения ошибок кодирования, которая прямо пропорциональна числу кодируемых символов. Внутреннее же описание модели 2 зависит от класса используемой ЭВМ и размеров конкретных задач.
6. Теория гиперграфов является новой ветвью математики, и соответствующий математический аппарат в настоящее время создается.
7. Гиперграф является обобщением обычного графа. Поэтому от описания модели 2 можно всегда перейти к описанию модели 1.
Модель 3 (ультраграф схемы).
'В данной модели схеме ставится в соответствие ультраграф G (Z' V'). Ультраграф является обобщением ориентированных графов и гиперграфов. Считают, что задан ультраграф G(Z' V'), если задано множество вершин Z'=ZV и множество ориентированных ребер V'.
В модели З каждому ребру ультраграфа (как и в модели 2) взаимнооднозначно соответствует некоторая электрическая цепь схемы. Каждое ребро ультраграфа «ориентируется» в соответствии с порядком прохождения сигналов в схеме. При описании ультраграфа и его изображения удобно использовать его представление в виде ориентированного графа Кенига (см. рис.).
Ультраграф может быть задан:
- в виде двух пар альтернативных списков
а) T(zi) – подмножеств ребер УГ таких, что
![]()
![]() tf
T(zi)
существует ребро (zi
tf)
V'
- вершина
zi
- источник сигнала,
tf
T(zi)
существует ребро (zi
tf)
V'
- вершина
zi
- источник сигнала,
б) T'(ti) – подмножеств ребер таких, что
![]() tf
T'(tf)
существует ребро (tf
zi)
V'
- вершина
zi
- приемник сигнала.
tf
T'(tf)
существует ребро (tf
zi)
V'
- вершина
zi
- приемник сигнала.
Или
а) Z(tf) – подмножество вершин таких, что
![]() Zi
Z(tf)
существует ребро (tf
zi)
V'
– вершина
tf
- источник сигнала,
Zi
Z(tf)
существует ребро (tf
zi)
V'
– вершина
tf
- источник сигнала,
б) Z'(tf) подмножество вершин таких, что
![]() zi
Z'(tf)
существует ребро (zi
tf)
V'
– вершина
tf
- приемник сигнала
zi
Z'(tf)
существует ребро (zi
tf)
V'
– вершина
tf
- приемник сигнала
Пример:
T(K1)={t1}, T'(K1)={0}, T(X3)={ t5 t6 }, T'(X3)={ t1}, T(X6)={o}, T'(X6)={t2 t5 t7}
Таким образом, модулю zi инцидентны цепи, входящие в состав подмножеств T(zi) и T'(zi), т. е. Tzi=T(zi) T'(zi).
Подмножества Z(tf) и Z'(tf) записываются аналогично:
- в виде пары матриц
||δif||T(Z) и ||δif||T'(Z), где
{
{
δif T(zi) = 1, если tf T(zi) δif T'(zi) = 1, если tf T'(zi)
0 0
Характеристики модели 3
1. Модель можно использовать для решения основных задач конструкторского проектирования. При этом одним из основных достоинств модели является возможность предварительного проведения временного моделирования схемы с дальнейшим учетом его результатов в виде ряда ограничений ,и весовых коэффициентов, используемых на всех этапах проектирования.
2. На основании модели можно точно определить все основные конструктивные параметры устройства. Отметим, что особенно просто при этом определяются задержки сигналов в цепях схемы. Поэтому при решении конструкторских задач в качестве показателя качества наиболее целесообразно использовать величину суммарных задержек в цепях. В случае применения других показателей качества проектирования можно воспользоваться более простыми моделями.
3. Все алгоритмы решения конструкторских задач достаточно простые и, как правило, совпадают с алгоритмами обработки модели 1.
4. Если в схеме для каждого компонента известны сигналы, на него поступающие, и сигналы, им генерируемые, то переход от схемы к ультраграфу является однозначным и не сложным.
5. Исходная информация об ультраграфе вводится в виде списков ненулевых элементов (как в случае применения гиперграфов), а внутреннее описание может быть представлено и в виде матриц инциденций. В последнем случае требуемый объем памяти возрастает вдвое по сравнению с аналогичным описанием гиперграфа.
6. Теоретический аппарат, базирующийся на ультраграфах, в настоящее время только зарождается.
7. От описания модели 3 всегда можно перейти к описанию моделей 2 и 1.
