1 , Если tf t(xj)
jf =
0
В этом случае для любой вершины xj X\X1 указанная оценка записывается
в
{
δgsf
xj)}
Δ
Kj
=
jf
*(g'f
– pf),
где g'f
= 0
Таким образом, g'f = 1 только тогда, когда ребро tf, кроме вершины xj, инцидентно хотя бы одной вершине оставшейся в X\X1. Т.е., электрическая цепь, представленная ребром tf, при переносе xj в подмножество X1, связывает X1 с X\X1 (связь между двумя блоками).
Величина pf = 1 в том случае, если хотя бы одна вершина, инцидентная tf, уже включена в подмножество X1.
Таким образом, оценка Kj отражает изменение числа электрических соединений (связывающих вершины из X1 и X\X1) при переносе модуля xj из одного подмножества X\X1 в подмножество X1. Эта величина может принимать положительные, отрицательные значения и нуль.
Исходя из смысла оценки Kj, на каждом шаге работы алгоритма в подмножество X1 можно включать ту вершину xj X\X1, для которой значение Kj отрицательно и имеет максимальное значение по модулю.
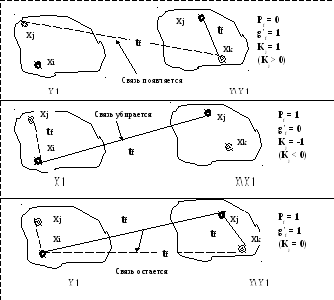
Рис. Геометрическая интерпретация работы алгоритма разрезания гиперграфа
Сформулируем алгоритм разрезания гиперграфа и приведем пример.
П1. В подмножество Х1 включается к.-н. вершина xi X (например модуль схемы с максимальным числом связей с другими модулями схемы. Задается мощность множества X1 |X1| = N1.
П2. Вычисляются оценки Kj для всех оставшихся вершин xj X\xi. Выбирается вершина с максимальным отрицательным значением Kj и эта вершина включается в подмножество Х1.
П3. Вычисляется мощность множества |X1|. Если это число равно заранее оговоренному допустимому числу вершин в формируемом множестве |X1| = N1, то Конец. Если |X1| < N1, то переход к П2.
П4. Конец.
Пример.
Пусть КС задана в виде матрицы инциденций. Требуется разбить множество модулей схемы на два подмножества с числом модулей |X1| = 3, |X\X1| = 2.
|
x\t |
1 |
2 |
3 |
4 |
5 |
6 |
∑tf |
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
3 |
|
2 |
1 |
0 |
1 |
1 |
0 |
0 |
3 |
|
3 |
0 |
1 |
0 |
0 |
1 |
1 |
3 |
|
4 |
1 |
1 |
0 |
1 |
0 |
0 |
3 |
|
5 |
1 |
1 |
1 |
1 |
0 |
0 |
4 |
||if||=
Решение.
П1. Включим в формируемое подмножество вершину х5 с максимальным числом связей - 4, т.е. Х1 = {x5}.
П2. Вычисляем Kj для оставшихся вершин в подмножестве X\X1 (j = 1,2,3,4).
K1 = 0+1+1=2, K2 = 0+(-1)+0 = -1, K3 = 0+1+1 = 2, K4 = 0+0+0 = 0.
В подмножество X1 включаем вершину х2, т.е. X1 = {x2 x5}. Повторяем П2.
П2. Подсчитываем Kj для оставшихся вершин в X\X1:
K1 = 0+1+1 = 2, K3 = 0+1+1 = 2, K4 = -1+0+(-1) = -2.
В подмножество X1 включаем вершину х4, т.е. Х1 = {х2 х4 х5}.
Множества Х1 и Х\Х1 сформированы: в них три и две вершины соответственно.
X1 X\X1
Рис. Результат разбиения
В результате разбиения два подмножества соединяет только одна цепь t2.