
- •Компьютерные технологии проектирования вычислительных устройств
- •Структура сапр
- •1. Математические модели конструкций и схем ву
- •Модель компонента
- •Модели электрических схем
- •Компьютерные технологии проектирования печатных плат в среде p-cad Создание символов компонентов
- •Конструкторско-технологические параметры печатных плат
- •Отверстия печатных плат
- •Стеки контактных площадок (Pad Stacks) и переходных отверстий (Via Stacks).
- •Создание на пп посадочных мест компонентов.
- •Создание схемы электрической принципиальной
- •2). Размещение модулей на мкп
- •Алгоритмы и модели компоновки ву
- •Критерии оптимизации при разрезании электрической схемы
- •1 , Если tf t(xj)
- •Итерационный алгоритм разбиения гиперграфа
- •Пример алгоритма типизации.
- •Покрытие функциональных схем модулями заданного библиотечного набора
- •Задача размещения модулей.
- •Размещение компонентов в регулярном монтажном пространстве
- •Размещение компонентов в нерегулярном монтажном пространстве
- •Алгоритм последовательного размещения
- •Метод силовых функций (непрерывно – дискретный алгоритм размещения)
- •Задача "перераспределения" выводов модуля
- •Подсчет изменения суммарной длины связей в итерационных алгоритмах
- •Трассировка электрических соединений
- •Математическая формулировка задачи трассировки электрических соединений.
- •Алгоритмы трассировки
- •Эвристический алгоритм трассировки. Двухлучевой алгоритм трассировки
Трассировка электрических соединений
Трассировка соединений является, как правило, заключительным этапом конструкторского проектирования ПП и состоит в определении проводящих линий, соединяющих эквипотенциальные контакты компонентов, составляющих проектируемое устройство.
Задача трассировки — одна из наиболее трудоемких в общей проблеме автоматизации проектирования ВУ. Это связано, в частности, с многообразием способов конструктивно-технологической реализации соединений, для каждого из которых при алгоритмическом решении задачи применяются специфические критерии оптимизации и ограничения.
С математической точки зрения трассировка — наисложнейшая задача выбора из огромного числа вариантов оптимального решения.
Одновременная оптимизация всех соединений при трассировке за счет перебора всех вариантов практически невозможна. Поэтому разрабатываются в основном локально оптимальные методы трассировки, когда при наличии ранее проведенных соединений трасса оптимальна лишь на данном шаге.
Основная задача трассировки формулируется следующим образом: по заданной схеме соединений проложить необходимые проводники на плоскости (плате, ТЭЗ, кристалле и т. п.), чтобы реализовать заданные электрические соединения с учетом заранее заданных ограничений. Основными являются ограничения на ширину проводников и минимальные расстояния между ними.
Исходной информацией для решения задачи трассировки соединений обычно являются список цепей, параметры конструкции элементов и коммутационного поля, а также данные по размещению элементов.
Критериями трассировки могут быть:
процент реализованных соединений,
суммарная длина проводников,
число пересечений проводников,
число монтажных слоев,
число межслойных переходов,
равномерность распределения проводников,
минимальная область трассировки и т. д.
Часто эти критерии являются взаимоисключающими, поэтому оценка качества трассировки ведется по доминирующему критерию при выполнении ограничений по другим критериям.
Задача трассировки всегда имеет топологический и метрический аспекты.
Топологический аспект связан с выбором допустимого пространственного расположения отдельных фрагментов соединений без фиксации их конкретного месторасположения при ограничениях на число пересечений и слоев и т. п.
Метрический аспект предполагает учет конструктивных размеров элементов, соединений и коммутационного поля, а также метрических ограничений на трассировку.
В известных алгоритмических методах решения задачи трассировки метрический аспект присутствует всегда, а топологический — в большей или меньшей степени. Все существующие методы трассировки можно подразделить на две большие группы: последовательные и параллельные.
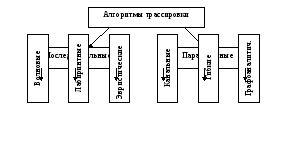
Рис. Классификация алгоритмов трассировки
К волновым относятся алгоритмы, основанные на идеях динамического программирования на дискретном рабочем поле (ДРП). В настоящее время разработано огромное число модификации волнового алгоритма, предложенного Ли еще в 1961 г., однако все они сохраняют его основной недостаток: большие объемы вычислений и памяти ЭВМ.
Эффективное использование волновых алгоритмов возможно лишь для ДРП с числом клеток не более 105. Число неразведенных трасс обычно не превышает 10%.
Основная идея лабиринтных алгоритмов состоит в отыскании пути между двумя ячейками ДРП посредством последовательного обхода преград в лабиринте, образованном занятыми и свободами ячейками. В отличие от волнового алгоритма поиск носит направленный характер, поэтому время поиска сокращается, алгоритмы обычно обеспечивают разводку около 80% соединений.
Эвристические алгоритмы трассировки эффективны, как правило, только на начальных стадиях трассировки, когда на плоскости мало преград. Основная идея состоит в генерации самых длинных отрезков в направлении цели с эвристическими приемами обхода препятствий.
А) В последовательных методах трассировки
трассы проводят одну за другой последовательно, при этом проведение какой-либо трассы а на (i—1)-м шаге может затруднить проведение трассы b на г-м шаге, так как является препятствием для проведения трассы b. Следовательно, особенно актуальным для последовательных алгоритмов трассировки является предварительное ранжирование (упорядочение) соединений до начала трассировки. Существуют различные стратегии упорядочения, основанные, в частности, на длине соединений, степени охвата соединением других соединений и др.
Однако объективных оценок эффективности таких методик в настоящее время нет, поэтому наиболее разумными представляются использование нескольких вариантов очередности и выбор из них наилучшего.
Задачу трассировки можно условно представить в виде четырех последовательно выполняемых этапов:
определение перечня соединений;
размещение по слоям;
определение порядка соединений;
трассировка проводников.
На первом этапе формируется точный список, указывающий, какие соединения (цепи или фрагменты цепей схемы) должны быть проведены (ЧТО проводить).
На втором этапе предпринимается попытка точно решить, ГДЕ (на каком слое) каждое соединение может располагаться.
На третьем этапе определяется последовательность проведения соединений для каждого слоя, т. е. указывается, КОГДА каждый проводник, помещенный в этот слой, будет проведен.
На четвертом этапе дается ответ, каким (КАК, каким алгоритмом) образом должно быть проведено каждое соединение.
Рассмотрим указанные этапы подробнее.
Исходная информация для первого этапа—это перечень соединений контактов каждого элемента с контактами других элементов. Одиночные контактные соединения записываются непосредственно в перечень соединений (матрицу цепей или список). Трудность при реализации возникает тогда, когда один контакт необходимо соединить с несколькими контактами. Для решения этого вопроса используют алгоритмы построения кратчайших покрывающих деревьев Прима или Штейнера. На этом этапе программа-трассировщик не производит соединений, она только определяет, какие проводники должны быть растрассированы.
При определении перечня соединений необходимо также решать вопросы распределения контактов элементов по контактам разъема.
Часто на практике пытаются исключить пересечение при проведении прямых линий между контактами элементов и соответствующими им контактами разъема. При трассировке многие элементы имеют логически эквивалентные контакты. Поэтому для упрощения трассировки просматривают проводники, подходящие к таким контактам, и при необходимости заменяют их друг на друга. Правило при замене проводников обычно заключается в исключении пересечений прямых линий.
Пример. Списки соединений, формируемые в текстовом файле *.alt.
1: D1/1 D5/3 X1/7 ;
GND: D1/7 D5/8 X1/12;
Задача размещения проводников по слоям. Она сводится к построению плоской укладки графа КС. Окончательный вариант размещения по слоям можно улучшить, если проанализировать каждый проводник.
Т.к. в большинстве случаев трассы состоят из горизонтальных и вертикальных отрезков, то прямые линии, проведенные между двумя контактами, и пересекающиеся между собой, не всегда пересекаются при использовании метрики
Dij = |zi – zj| + |yi – yj|
Однако, пересечение евклидовых прямых указывает на потенциальный "конфликт" между вершинами этой пары.
Обычно проблему размещения соединений по слоям рассматривают как задачу раскраски специального графа.
Информацию о том, какие проводники пересекаются можно задать в форме графа пересечений, в котором вершина означает проводник, а ребро – наличие потенциального пересечения.
Хроматическое число графа указывает наименьшее количество "цветов", с помощью которых можно "окрасить" его вершины таким образом, чтобы в нем не было ни одной дуги, которая соединяла бы вершины одного и того же цвета.
В примере – хроматическое число равно 3.
Раскраска узлов графа пересечений соответствует назначению каждого проводника в соответствующий (раскрашенный) слой.
Т.е., минимальное число слоев, которое требуется для распределения в них проводников без пересечений равно хроматическому числу графа.
Теорема Кенига: Граф может быть раскрашен в два цвета, если в нем не имеется циклов нечетной длины.
На третьем этапе производится исследование каждого слоя с целью точного определения момента, когда можно будет трассировать каждый проводник. Другими словами — определить очередность прокладки проводников в каждом слое.
Сформулируем общее эвристическое правило Айкерса о порядке трассировки проводников. Проводники трассируются в порядке приоритетных номеров. Приоритетный номер электрической цепи - обратный числу контактов, попавших в прямоугольник зоны реализации этой электрической цепи.
Пример.
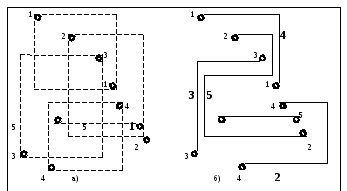
На Рис.а) показаны зоны реализации электрических цепей.
В Таблице установлено число контактов других цепей, попавших в зону реализации отдельной цепи и очередность прокладки трасс.
|
Номер цепи |
Число контактов в зоне реализации |
Очередность проведения |
|
1 |
2 |
4 |
|
2 |
4 |
5 |
|
3 |
1 |
3 |
|
4 |
1 |
2 |
|
5 |
0 |
1 |
На Рис. б) показана приблизительная трассировка цепей.
После того как все соединения распределены по слоям и определен порядок их обработки, решается задача трассировки фрагментов всех цепей, что и выполняется на четвертом этапе.
На практике короткие горизонтальные и вертикальные отрезки проводников трассируются первыми, далее трассируются окружающие их почти вертикальные и горизонтальные проводники. В заключение трассируются длинные соединения, которые по отношению к другим чаще располагаются с внешней стороны.
Четвертый этап трассировки является основным, наиболее трудоемким, определяющим эффективность и качество всей задачи трассировки. На рис. приведена классификация алгоритмов трассировки этого этапа.
Б) Параллельные алгоритмы трассировки.
В параллельных алгоритмах трассировки вначале определяется допустимое взаимное расположение трасс, которое оптимизируется по выбранному критерию, и лишь потом трассы фиксируются на коммутационном поле.
Канальные алгоритмы основаны на возможности в некоторых случаях регулярного разбиения коммутируемого поля (КП) на каналы трассировки. Внутри каналов проводятся вертикальные и горизонтальные отрезки цепей. Алгоритмы работают быстро, однако для них актуальна проблема качества получаемых решений. Отметим, что канальным алгоритмом свойствен иерархический подход к трассировке, когда исходная задача декомпозируется на несколько подзадач. При этом на каждом иерархическом уровне в зависимости от его специфики целесообразно применение различных методов трассировки.
В алгоритмах гибкой трассировки на первом этапе строятся модели топологии для трасс цепей на дискретном топологическом рабочем поле (ДТРП) (без жесткой фиксации), а на втором этапе—модели геометрии, которые метрически точно определяют конфигурацию и месторасположение каждой трассы на КП.
В графотеоретических методах используют графовые модели элементов и компонентов схем, на основе которых синтезируется топологический эскиз проектируемого устройства. На следующем этапе решается задача метризации топологического эскиза.
Для волновых и лабиринтных методов используется ДРП следующего вида.
Пусть задана прямоугольная система координат SOT на КП и выбраны единицы измерения hs и ht соответственно вдоль осей OS и ОТ. Проведем через точки осей с координатами lhs и lht, где l=1, 2, ..., прямые, параллельные осям координат.
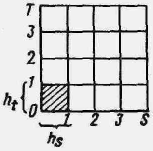
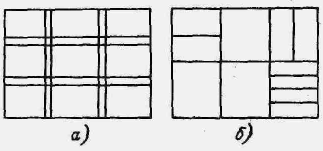
Рис. Модель КП: Модель КП: а) регулярное разбиение,
для волновых и 6) нерегулярное разбиение
и лабиринтных алго-
ритмов трассировки
Тогда плоскость КП может быть разбита на элементарные прямоугольные ячейки размером hs x ht, а прямые разбиения образуют координатную сетку с шагом hs по оси OS и шагом ht по оси ОТ. Совокупность элементарных ячеек, на которые разбивается КП, называется ДРП. Значения hs и ht выбираются в зависимости от площади КП, допустимой плотности расположения выводов элементов и проводников.
Модель КП для_канальных и эвристических алгоритмов, так же как и в предыдущем случае, разбивается на прямоугольные области, называемые каналами, но в отличие от предыдущей модели разбиение определяется расположением выводов элементов. Если элементы однотипны и размещены на плоскости регулярно, то разбиение на каналы также будет регулярным, в противном случае—нерегулярным (рис. а, б).
Длина стороны любого канала, параллельной преимущественному направлению трасс на слое, называется длиной этого канала, а длина другой стороны—его шириной. Число трасс, которые могут пересечь боковую границу канала, называется пропускной способностью канала.
Регулярное разбиение КП на прямоугольники не вызывает затруднений. Нерегулярное разбиение несколько сложнее. Желательно, чтобы прямоугольников разбиения было как можно меньше, так как при этом уменьшается время трассировки, также размеры таблиц для представления данных.
Для описания топологии трасс в методах гибкой трассировки строится ДТРП. Ее можно представить в виде графа Gr = (Xr, Ur), где Хr соответствует контактам элементов, характерным точкам края платы, внешним контактам, запрещенным зонам; Ur—линиям, соединяющим элементы х Хг.
Вообще, дискретами могут быть грани любой конфигурации. При этом ненасыщенные трассами грани могут сжиматься, а те, через которые проходит большое число трасс, - растягиваться.
