Математика 3 семестр

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Государственный аграрный университет Северного Зауралья

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

cos x sin xdx.

.pdf

Скачиваний:

Добавлен:

14.04.2015

Размер:

2.31 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 119 10 11 > Следующая >>>

6.Какие знакопеременные числовые ряды называются абсолютно сходящимися и какие условно сходящимися?

7.В чём заключается интегральный признак сходимости числового ряда?

8.Сформулировать один из признаков сравнения числовых рядов.

9.В чём заключается задача разложения функции f(x) в степенной ряд?

10.Как найти интервал сходимости степенного ряда

11.Как определяются коэффициенты ряда Тейлора?

12.Запишите остаточный член ряда Тейлора.

13.Какой ряд называется рядом Маклорена?

14.В чём состоит метод интегрирования дифференциальных уравнений с помощью степенных рядов?

15.В чём состоит метод интегрирования функции с помощью степенных рядов?

КОНТРОЛЬНАЯ РАБОТА № 2.

В ЗАДАЧАХ 111-120 найти неопределённые интегралы способом подстановки (методом замены переменной).

115.e x2 xdx.

112.

114.

116.

118.

120.

3	dx	.
ln x	x	.
	x

cos x dx. 3 sin x

	x		dx.
2	x	4

	x	dx.

	1 2x	2

xdxln x .

В ЗАДАЧАХ 121-130 найти неопределённые интегралы применяя метод интегрирования по частям.

121.

123.

125.

127.

ln xdx.

x 1 e2 x dx

arctg2xdx.

8x 2 sin 5xdx.

122.

124.

126.

128.

2x 1 sin 3xdx.

x cos2xdx.

5x 1 ln xdx.

x 3 e 2 x dx.

129.		x ln 3xdx.

В ЗАДАЧАХ 131-140 разложением рациональных

130.

найти неопределённые дробей на простейшие.

2x 8 e	7 x	dx.

интегралы, пользуясь

131.

133.

135.

137.

139.

			x	dx.
	x	3		dx.
	x		1
		3x 1
x x 2				1
						dx.
	3x 1
					dx.
	x3 3x				dx.
			7x 2					dx.
x				3 x 2			1	dx.
x				3 x 2			1
x				3x				dx.
				1 x 2			3	dx.
				1 x 2			3

132.

134.

136.

138.

140.

x 20				dx.
x		3	8

2x 5				dx.
x	3		2x

8x 5			dx.

x 1 x 2 2
	5x 11
x x 2 4
			dx.
	2x
		dx.
	x3 1

В ЗАДАЧАХ 141-150 вычислить определённые интегралы.

	2			1
141.	ln x 2	4 dx	142.	3x 2 arcsin x dx
	0			0

143.

145.

147.

149.

П
4
x	2	sin 2x			dx
x		sin 2x			dx
0
1
2
arcsin 2x dx
0
0
2x 3 e					2 x	dx
2x 3 e						dx
1
П			x
x cos			x	dx
x cos			2	dx
0			2
0

			2							x
144.					arctg					x	dx
					arctg					2	dx

			0
			0
			1
146.					x		3	arctgx dx
					x			arctgx dx

			0
	2						ln x 1 dx
148.		3x		2
		3x

	1
		e	ln			2		x
150.			ln					x	dx.
				x			2		dx.
							2
		1
		1

В ЗАДАЧАХ параболами.

151.	y	1
	y	2

151-160

x	2	x 1;

вычислить площадь, ограниченную заданными

y 12 x2 3x 6;

152.

153.

154.

155.

156.

157.

158.

159.

160.

y	1	x	2	x 2.

	2

y1 x 2 3x 2; 3

y 2x2 6x 3;

y 3x			2	5x 1;

y x	2		3x 1;

y 2x		2		6x 1;


y	1		x 2 2x 4;

3
y x2				5x 3;
y x		2		2x 5;

y		1		x		2	5x 7.

		2

y		2		x	2		2x 4.

		3

y x2				x 5.
y x		2		2x 1.

y x		2		2x 5.

y x		2	x 1.

y	2	x 2				x 2.
	3

y 3x		2	2x 1.

y x	2	x 1.

В ЗАДАЧАХ 161-170 вычислить расходимость.

						dx
161.						dx
161.		x	2	4x 13
	1	x		4x 13
	1
									3
		x	2	e		x			3	dx
163.			2			x


	0
			x dx
165.			x dx
165.		x						3
	0	x		2
	0
	3			dx
167.				dx
167.		x		3				2
	0	x		3
	0
							2
		x	e		x		2		dx
169.					x


	0

несобственные интегралы и установить их

					dx
162.					dx
162.						3
	e		x ln x
	e
					2dx
164.					2dx
164.			x	2	2x 2
	0		x		2x 2
	0
	2		x		dx
166.			x		dx
166.			4 x			2
	0					2
	0
	e				dx
168.					dx
168.		x			ln x
	1	x			ln x
	1
				dx
170.				dx
170.					4
	0	x 3
	0

В ЗАДАЧАХ 171-180 найти общее решение (общий интеграл) дифференциальных уравнений первого порядка.

171.

173.

175.

177.

179.

y	x 8y				;
	8x y

y	x y			;
	x y

xy y ln			y		0;
			x

xyy	x	2	y			2	;

xy y ln2 xy 0;

172.

174.

176.

178.

180.

xyy x

;

xy xtg

sin

;

x y y 2x y;

xy ln

x y ln

;

В ЗАДАЧАХ 181-190 найти частное решение дифференциального уравнения,

удовлетворяющего указанному начальному условию.

181.	y 2xy 3x 2 e x2				y (0)=0;
181.					y (0)=0;
182.	xy y y	2	sin x,				;
182.	xy y y		sin x,		y	2	;
					2	2
183.	y 2xy x ln xe x2			,	y(1)=0;
183.					y(1)=0;

184.

185.

186.

187.

188.

189.

190.

yctgx

sin x

sin x,

;

y cos2

x y tgx,

y (0)= -1;

y xy

;

y (1)=1;

1 x

y y y

arctgx,

y (0)= 1;

y (0)=0;

xy y x

cos x,

;

В ЗАДАЧАХ 191-200 найти: а) частное решение линейного одноро-дного дифференциального уравнения второго порядка с постоянными коэффициентами,

удовлетворяющее заданным начальным условиям; б) общее решение линейного неоднородного дифференциального уравне-ния второго порядка с постоянными коэффициентами.

191.

а)

7 y 10y 0;

y 0 2;

б)

y 2y 3x

192.

а)

10y 0;

y 5y 6y 2xe

б)

;

193.

а)

y 0 1;

y 8y x 1 e

б)

;

194.

а)

y 8y 7 y 0;

y 0 2;

б)

y 6y 8y 3e4x ;

195.

а)

9y 0;

y 0;

б)

y 2y 3y xe x ;

196.

а)

y 7 y 12y 0;

y 0 2;

б)

y y 2y x 2 e 2x

y	/	0 1;


			1;
y
	2

y / 0 0;

/	0 1;
y

y	1;
/

y / 0 2;

197. а)

б)

198. а)

б)

199. а)

б)

200. а)

б)

y 9y 0;

y 2y 8y 3x
y 3y 2y 0;
y 7y 2x	2	x;

y 5y 6y 0;
y y 8x	e		;
2		x
y 2y 5y 0;
y 3y 10y 2x

y 0 1;1 e2x y 0 0;

y 0 5;

y 0 1;

2	e	x	;

y	0 3;
/
/	0 1;
y	0 1;

y / 0 0;

В ЗАДАЧАХ 201-210: а) исследовать на сходимость с помощью признака Даламбера знакоположительный ряд; б) исследовать на сходимость с помощью признака Лейбница знакочередующийся ряд; в) найти радиус сходимости степенного ряда и определить тип сходимости ряда на концах интервала сходимости.

201. а)

202. а)

203. а)

204. а)

205.а)

206. а)

207. а)

208. а)

209.а)

210. а)

	2		n
	2				;
	n		2		;
n 1	n
n 1
				1
				1			;
	n5				n 1		;
n 1	n5
n 1
						1
						1

n 1		n 2 5
n 1
				n
				n			;
		3		n 2			;
n 1		3
n 1
	3		n
	3				;
	n		2		;
n 1	n
n 1
					1
					1
	n 1 7								n
n 1	n 1 7
n 1
		7			n
		7					;
	n 3						;
n 1	n 3
n 1
				2		n
				2					;
	1 n							2	;
n 1	1 n

n 2

2n ;

n 1

5n 1

n2 ;

n 1

n	;

;

б)

;

n 1

1 n

;

n 1

;

n 1

;

n 1

;

n 1

;

n 1

1 n

;

n 1

;

n 1

1 n

;

n 1

1 n

;

n 3

n 1

в)

n x

;

n 1

;

n 1

;

n 1

;

n 1

;

n 1

;

n 1

x n ;

n 1

;

n 1

;

n 1

;

n7n 1

n 1

Раздел 9. ТЕОРИЯ ВЕРОЯТНОСТЕЙ

9.1Случайные события. Вероятность событий

1.Определение. Вероятностью события А в данном испытании называется число,

выражающее меру объективной возможности появления этого события.

	( A)	m
	( A)	n
		n

- классическая формула для вычисления вероятности события А, где m-

число исходов испытания, благоприятствующих событию А, n- число всех единственно возможных, несовместных и равновозможных исходов испытания. Р(А) - вероятность события А.

3.Р(А)=0, если событие А- невозможное событие.

4.Р(А)=1, если событие А- достоверное событие.

5.0 Р(А) 1, если событие А- случайное.

6.Р(А+В)=Р(А)+Р(В), если события А и В несовместны.

Если А и А - противоположные события, то Р(А)+Р A =1- сумма

вероятностей двух противоположных событий.

(А+ А )- событие достоверное,

А и А - события несовместные.

Если события А и В независимы, то Р(А В)=Р(А) Р(В), где

событие (А В)

–

произведение (совмещение) двух независимых событий А и В.

Если

события

зависимы

данном

испытании,

то

P( A B) P( A) PA (B) , где событие (А В)- произведение двух зависимых событий. PA (B) -

вероятность события В при условии , что событие А наступило.

10. Если события А и В совместны, то Р(А+В)= Р(А)+ Р(В)- Р(А В)

11.	P( A) P(B1 ) PB	( A) P(B2 ) PB	( A) ... P(Bn ) PB	( A);	где
	1	2	n

B1, B2 …,Bn- несовместные события или гипотезы. Событие А может наступить совместно с одной гипотез.

12.

PA (Bi)

P(B )P		( A)
1	B
	1

P(Bi) P			( A)
		Bi
P(B ) P		( A) ..
2	B
	2

P(B ) P
n	B
	n

( A)

- формула Бейеса, которая

позволяет переоценить вероятность гипотез после того как становится известным результат испытания в результате которого появилось событие А.

13.	P	C m	m q n m - формула Бернулли, где C m		n!

	m,n	n		n	m!(n

элементов по m в каждом. р =P(A), q =P				( A) . Используется

повторении испытаний . Событие А может появиться или не испытаний.

- число сочетаний из n m)!

формула Бернулли при появиться в каждом из n

14.

Pm,n

1 npq

(x)

Локальная формула Лапласа, где

m np

x ,

npq

P P(A),

q P( A),

n- число испытаний.

	(x)	1
	(x)	2П
		2П

	x	2
	x
e	2
e

- значения этой функции можно найти в

соответствующей таблице (см приложение 1) Локальная формула Лапласа используется при повторении испытаний, когда число их (испытаний) велико.

15.

Pn (m1

m m2 ) Ф(x2 ) Ф(x1 ) - интегральная формула Лапласа.

где

x	m np	;
x	1	;
	1
1	npq
	npq

x		m	2	np
x

	2			npq
				npq

	Ф(x)	1
	Ф(x)	2П
		2П

x	x	2
x	x
e	2
e

0

функция Лапласа, значения которой можно найти в

соответствующей таблице (приложение 2). Для x 5 полагают Ф(x)= 0,5; Ф(-x)=-Ф(x) -

функция нечётная. Используется интегральная формула Лапласа при повторении испытаний (n-велико).

16.

Pm,n


m
	e
m!	e
m!

- формула Пуассона, где

n p;

n- число испытаний, р= P(A)

Формула Пуассона применяется в тех случаях , когда n 10, p = P(A)- невелика.

9.2 Случайная величина

1. Определение. Переменная величина x называется случайной величиной, если в результате испытания она примет одно и только одно возможное значение, наперёд неизвестное и зависящее от случайных причин.

2. F(x)=P(X x), где x- заданное значение, событие (X x) означает, что случайная величина X примет значение левее точки x.

3. Производная от функции распределения (F (x)) называется плотностью распределения вероятностей непрерывной случайной величины.

Т.е. F (x)=f(x) - плотность вероятности непрерывной случайной величины.

4. F (x) f (x)dx нахождение функции распределения непрерывной случайной

величины X по её плотности распределения.

5. P(a x b)=

(x)dx

- вероятность попадания непрерывной случайной величины Х в

интервал (a,b). P(a x b)=F (b)-F(a)- для дискретной случайной величины.

n M ( X ) xi i 1

p	i

- математическое ожидание дискретной случайной

величины X

M ( X )

(центр распределения X ).

	b
		xf (x)dx - математическое ожидание непрерывной слу-чайной величины X,

	a

все значения которой


8.	M ( X )	xf (x)
8.	M ( X )	xf (x)

находятся в a,b .

dx -математическое ожидание непрерывной слу-чайной величины X в

случае, если значения её сплошь заполняют числовую ось (ox) ,где f(x) - плотность вероятности.

9.M(X-M(X))2=Д(X) - определение дисперсии дискретной случайной величины X.

10.M(X2)-(M(X))2=Д(X) - формула для вычисления дисперсии.

11. 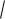Д ( X ) = ( X ) - среднее квадратическое отклонение случайной величины X.

12. Д ( X ) (x M ( X ))2 f (x)dx - определение дисперсии непрерыв-ной случайной

величины, где M(X) - математическое ожидание

f(x) - плотность вероятности

Д(X) - дисперсия непрерывной случайной величины X, если все её возможные значения сосредоточены на a,b .

13.


( X ) (x M ( X ))	2
( X ) (x M ( X ))

(x)dx

- дисперсия в случае, когда значения Н.С. В. сплошь

заполняют числовую ось (OX).

		b
14.	Д ( X )		x	2	f (x)dx (M ( X
				2

		a

))	2


Д ( X ) x	2
	2

(x)dx

(M ( X

))	2

формулы для вычисления дисперсии Н.С.В.
15.	k	M ( X k ) начальный момент k-го порядка.

M k		M ((x M ( X ))	k	) центральный момент k-го порядка.	k	и	M k	позволяют

лучше учесть влияние на математическое ожидание того возможного значения, которое велико и имеет малую вероятность.

16.

a	S

e	k

	M	3


	3

	M	4

		4

- асимметрия

3 эксцесс

aS	и ek оценивают

распределения.

отклонение теоретического распределения от нормального

17.Равномерное распределение.

Равномерным называется распределение таких случайных величин, все значения которых лежат на a,b и имеют постоянную плотность вероятности на этом отрезке (см. рис).

f(x)

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 119 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.11.20192.59 Mб14линия по пр-ву плавлен.сыра.doc
#
22.11.2019292.62 Кб8линия по сыру.docx
#
22.11.20195.47 Mб8линия по творогу.doc
#
14.04.2015135.17 Кб21лист достижения.doc
#
04.09.2019293.38 Кб13ЛР 3 Молотковые дробилки МШ Л.Р.№3.doc
#
14.04.20152.31 Mб39Математика 3 семестр.pdf
#
18.04.2019515.07 Кб12Мелиорация курсовая.doc
#
14.04.2015351.23 Кб95мелиорация.doc
#
23.09.201956.35 Кб5Менеджмент - методичка по курсовой.docx
#
14.04.201555.63 Кб7Мет указ по контр.раб для заочников.docx
#
22.11.2019108.54 Кб3МЕТЕОРОЛОГИЧЕСКИЕ ВЕЛИЧИНЫ.doc