Математика 3 семестр

Решение. Чтобы найти наибольшее, и наименьшее значения функции в заданной замкнутой области, необходимо:

1)найти стационарные точки, лежащие внутри области, и вычислить значения функции в этих точках; исследовать на экстремум эти точки не следует;

2)найти наибольшее и наименьшее значения функции на границе области; если граница состоит из нескольких линий, то исследование проводится для каждого участка в отдельности;

3)сравнить полученные значения функции и установить наибольшее и наименьшее значения функции в заданной замкнутой области.

Находим стационарные точки, лежащие внутри заданной области:

Приравняв нулю частные производные и решив полученную систему

2x 2 0, 4 y 8 0,

находим стационарную точку Р0(1; 2). Эта точка принадлежит заданной области. Вычислим значение функции в этой точке:

z P0 z 1;2 1 8 2 16 5 4

Граница области состоит из отрезка ОА оси Ох, отрезка 0В оси Оу и отрезка АВ. Определим наибольшее и наименьшее значения функции z на каждом из этих трех участков. На отрезке ОА

у = 0, а 0 x 4. Если у=0, то z(x) = х2 — 2x + 5. Находим наибольшее и наименьшее значения этой функции на отрезке [0, 4]:

z P1 z 1;0 4.

Вычислим значения функции на концах отрезка ОА, т. е. в точках 0(0; 0) и A(4; 0):

41

z(0) = 5, z(4)= 13.

На отрезке OB х = 0 и 0 y 4. Если х = 0, то z(y) = 2у 2 -8у + 5. Находим наибольшее и наименьшее значения функции z от переменной у на отрезке [0; 4]:

В точке О (0; 0) значение функции уже было найдено. Вычислим значение функции в точке В:

z(В) = z (0; 4) = 5.

Теперь исследуем отрезок АВ. Уравнением прямой АВ будет у = 4 - х. Подставив это выражениедля у в заданную функцию z, получим

Определим наибольшее и наименьшее значения этой функции на отрезке [0; 4]:

Рз — стационарная точка на отрезке АВ. Вычислим значение функции в этой точке:

Значения функции на концах отрезка АВ найдены ранее.

Сравнивая полученные значения функции z в стационарной точке Ро заданной области, в стационарных точках на границах области P1, Р2, Рз и в точках О, А и В,

Речь идёт о дифференцировании сложной функции.

42

Задача 13.

Исследовать на экстремум функцию z = - 4 + 6x-х2 –ху- у2.

Решение: Чтобы исследовать данную дважды дифференцируемую функцию z = f (x, у) на экстремум, необходимо:

Каждая пара действительных корней этой системы определяет одну стационарную точку исследуемой функции.

Пусть РО (Х0 , у0) одна из этих точек.

3. Составить и вычислить определитель второго порядка

4. Если в исследуемой стационарной точке Р0( X0, y0) >0, то функция z = f(x, у) в этой точке имеет максимум при A<0 и минимум при A>0; если <0, то в исследуемой точке нет экстремума.

Если = 0, то вопрос об экстремуме требует дополнительного исследования.

Находим стационарные точки заданной функции:

Следовательно, данная функция имеет только одну стационарную точку Ро(4, - 2). Находим частные производные второго порядка и их значения в найденной стационарной точке:

Как видно, частные производные второго порядка не содержат х, они постоянны в любой точке и, в частности, в точке Р0(4, -2). Имеем А = -2; В = - 1; С=-2.

Так как >0 и A<0, то в точке Ро(4; -2) данная функция имеет максимум:

4.5Вопросы для самопроверки

1.Сформулировать определение производной.

2.Каков геометрический смысл производной?

3.Как составить уравнение касательной?

4.Каков геометрический и механический смысл производной?

5.Как найти производную неявной функции? Параметрической функции?

6.Функция непрерывна в т. x0. Следует ли отсюда дифференцируемость функции?

7.В чём заключается геометрический смысл дифференциала функции?

Записать формулу, используемую в приближённых вычислениях. Найти приближённое

8.Сформулируйте определения функции двух, трёх переменных.

9.Каков геометрический смысл функции двух независимых переменных?

10.Что называется областью существования (определения) функции двух переменных?

11.Что называется пределом функции двух независимых переменных?

12.Сформулируйте определение непрерывности функции двух переменных в точке и в области.

13.Что называется частным приращением функции двух переменных? 14. Полным приращением функции двух (нескольких) переменных?

15.Дайте определение частной производной функции двух (нескольких) переменных. Укажите геометрический смысл частных производных функции двух переменных.

16.Что называется частным дифференциалом функции двух переменных и каков его геометрический смысл?

17.Что называется полным дифференциалом функции двух (нескольких) переменных? Каков геометрический смысл полного дифференциала функции двух переменных?

Раздел 5. Приложения производной функции

5.1 План исследования функции и построения графика

1.Найти область определения функции. Решение этого вопроса указывает на те интервалы оси (ОХ), над которыми пройдёт график и на те значения аргумента x, над которыми график не пройдёт, а также в каких точках пройдут вертикальные асимптоты.

2.Исследовать на чётность, нечётность. Решение этого вопроса облегчает построение. 3.Указать промежутки монотонности функции и найти экстремумы её, точки

экстремумов. Построить соответствующие точки на координатной плоскости.

4.Указать точки перегиба графика функции и нанести их на координатную плоскость. Указать промежутки выпуклости, вогнутости.

44

5.Найти уравнения вертикальных и наклонных асимптот, используя условия для существования этих асимптот. Построить эти линии на координатной плоскости.

6.Найти точки пересечения графика функции с осями координат. Нанести их на плоскость.

7.Исследовать поведение функции на концах области определения. Это поможет при построении графика.

8.Можно взять несколько контрольных точек, в случае уточнения поведения графика. 9.Построить график.

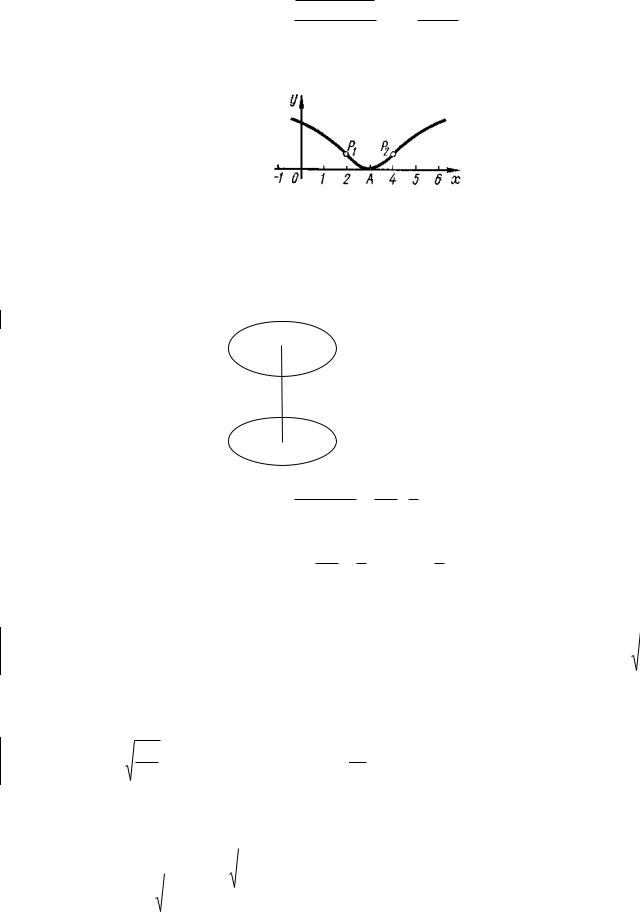
Задача. Исследовать функцию у = 1п(х2 — 6х +10) и построить ее график.

Решение:

1.Определим область существования функции. Квадратный трехчлен, стоящий под знаком логарифма, можно представить так: х2—6x+10=(x-3)2 + 1. Как видно, под знаком логарифма будет положительное число при любом значении аргумента х. Следовательно, областью существования данной функции служит вся числовая ось.

2.Исследуем функцию на непрерывность. Функция всюду непрерывна и не имеет точек разрыва.

3.Установим четность и нечетность функции. Так как у(-х) у(х) и у(- х) - у(х), то функция не является ни четной, ни нечетной.

4.Исследуем функцию на экстремум. Находим первую производную:

Знаменатель х2- 6x+10>0 для любого значения х. Как видно, при х < 3 первая

Итак, A(3; 0) - точка минимума . Функция убывает на интервале (- , 3) и возрастает на интервале (3, + ).

5. Определим точки перегиба графика функции и интервалы выпуклости и вогнутости

Разобьем всю числовую ось на три интервала: ( - , 2), (2, 4), (4, + ). Как видно, в первом и третьем интервалах вторая производная отрицательна, а во втором интервале

Следовательно, P1(2; ln 2) и P2(4; ln 2) — точки перегиба графика функции. График является выпуклым в интервалах ( - , 2) и (4, + ) и вогнутым в интервале (2, 4).

6. Определим уравнения асимптот графика функции. Для определения уравнения асимптоты y=kx+b воспользуемся формулами:

Чтобы найти искомый предел, дважды применяем правило Лопиталя:

45

5.2 Использование производной в задачах прикладного характера

Задача. Найти такой цилиндр, который имел бы наибольший объём при данной полной поверхности S.

Решение: Пусть радиус основания цилиндра равен x, а высота равна y.

46

Ответ: Цилиндр с квадратным сечением имеет наибольший объём при данной полной поверхности S.

План действий при решении задач прикладного характера.

1.Обозначить некоторую неизвестную величину прикладной задачи переменной x.

2.Записать ту величину, которая должна быть по условию наименьшей ( наибольшей ) как функцию переменной x.

3.Исследовать полученную функцию на экстремум, используя производные 1-го порядка и второго порядка, найти значение x, соответствующее точке экстремума исследуемой функции.

4.Записать ответ, вернувшись к прикладному значению x.

5.3 Примеры решения задач

Задача. Найти наибольшее и наименьшее значения функции:

f 1 8 0

f 1 8 0

В точке x=0 функция имеет максимум, равный f(0)=3.

В каждой из точек x=-1 и x=1 функция имеет минимум, равный f (-1)=f (1)=2 Найдём значения функции на концах сегмента :

f 2 f 2 11.

Итак , наибольшее значение равно 11, а наименьшее 2.

47

5.4Вопросы для самопроверки

1.Сформулируйте признаки возрастания (убывания) функции. Приведите примеры.

2.Дайте определение экстремума функции.

3.Как найти максимум, минимум функции (два правила)?

4.Приведите пример, когда обращение производной в нуль не является достаточным условием экстремума функции.

5.Как найти интервалы выпуклости (вогнутости) функции? Примеры.

КОНТРОЛЬНАЯ РАБОТА № 1.

В ЗАДАЧАХ 1 –10 решить заданную систему уравнений, пользуясь формулами Крамера. Сделать проверку полученного решения.

В ЗАДАЧАХ 11-20 даны координаты вершин треугольника ABC. Найти: 1) длину стороны AB; 2) уравнения сторон AB и BC и их угловые коэффициенты; 3) внутренний угол B в радианах с точностью до 0,01; 4) уравнение медианы AE; 5) уравнение и длину высоты CD; 6) уравнение прямой, проходящей через точку E параллельно стороне AB.

В ЗАДАЧАХ 21-30 даны координаты вершин пирамиды ABCD. Требуется:

1. записать векторы AB, AC, AD в системе орт i, j, k и найти модули этих векторов;

48

4.найти площадь грани ABC;

5.найти объём пирамиды ABCD;

27.A (1;3;1), B (-1;6;1), C (-1;3;7), D (1;6;9).

28.A (1;2;2), B (-1;5;2), C (-1;2;8), D (1;5;10).

В ЗАДАЧАХ 31-40 найти указанные пределы.

49

50