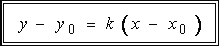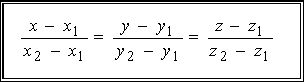- •1. Определение вектора. Длина вектора. Коллинеарность, компланарность векторов.
- •2. Умножение вектора на число. Свойства операции.
- •3. Сложение векторов, вычитание векторов.
- •4. Базис на плоскости. Теорема о разложении любого вектора по трём базисным векторам.
- •5. Базис в пространстве. Теорема о разложении любого вектора по трем базисным векторам.
- •6. Линейная зависимость векторов.
- •7. Декартова система координат на плоскости и в пространстве, координаты вектора.
- •8. Геометрический смысл координат вектора. Проекция вектора на координатные оси. Направляющие косинусы вектора
- •9. Деление отрезка в данном отношении.
- •6.4. Некоторые приложения скалярного произведения
- •11. Выражение скалярного произведения вектора через координаты сомножителей. Теорема.
- •12. Длина вектора, длина отрезка, угол между векторами, условие перпендикулярности векторов.
- •13. Векторное произведение векторов, его свойства. Площадь параллелограмма.
- •14. Смешанное произведение векторов, его свойства. Условие компланарности вектора. Объем параллелепипеда. Объём пирамиды.
- •15. Способы задания прямой на плоскости.
- •16. Нормальное уравнение прямой на плоскости (вывод). Геометрический смысл коэффициентов.
- •17. Уравнение прямой на плоскости в отрезках (вывод).
- •Приведение общего уравнения плоскости к уравнению плоскости в отрезках.
- •18. Уравнение прямой на плоскости с угловым коэффициентом (вывод).
- •19. Уравнение прямой на плоскости, проходящей через две точки (вывод).
- •20. Угол между прямыми на плоскости (вывод).
- •21. Расстояние от точки до прямой на плоскости (вывод).
- •22. Условия параллельности и перпендикулярности прямых на плоскости (вывод).
- •23. Уравнение плоскости. Нормальное уравнение плоскости (вывод). Геометрический смысл коэффициентов.
- •24. Уравнение плоскости в отрезках (вывод).
- •25. Уравнение плоскости, проходящей через три точки (вывод).
- •26. Угол между плоскостями (вывод).
- •27. Расстояние от точки до плоскости (вывод).
- •28. Условия параллельности и перпендикулярности плоскостей (вывод).
- •29. Уравнения прямой в r3. Уравнения прямой, проходящей через две фиксированные точки (вывод).
- •30. Канонические уравнения прямой в пространстве (вывод).
- •Составление канонических уравнений прямой в пространстве.
- •Частные случаи канонических уравнений прямой в пространстве.
- •Канонические уравнения прямой проходящей через две заданные точки пространства.
- •Переход от канонических уравнений прямой в пространстве к другим видам уравнений прямой.
- •31. Угол между прямыми (вывод).
- •32. Расстояние от точки до прямой на плоскости (вывод).
- •Расстояние от точки до прямой на плоскости – теория, примеры, решения.
- •Первый способ нахождения расстояния от заданной точки до заданной прямой на плоскости.
- •Второй способ, позволяющий найти расстояние от заданной точки до заданной прямой на плоскости.
- •Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости.
- •Расстояние от точки до прямой в пространстве – теория, примеры, решения.
- •Первый способ нахождения расстояния от точки до прямойaв пространстве.
- •Второй способ, позволяющий находить расстояние от точки до прямойaв пространстве.
- •33. Условия параллельности и перпендикулярности прямых в пространстве.
- •34. Взаимное расположение прямых в пространстве и прямой с плоскостью.
- •35. Классическое уравнение эллипса (вывод) и его построение. Каноническое уравнение эллипса имеет вид , где– положительные действительные числа, причём.Как построить эллипс?
- •36. Классическое уравнение гиперболы (вывод) и его построение. Асимптоты.
- •37. Каноническое уравнение параболы (вывод) и построение.
- •38. Функция. Основные определения. Графики основных элементарных функций.
- •39. Числовые последовательности. Предел числовой последовательности.
- •40. Бесконечно малые и бесконечно большие величины. Теорема о связи между ними, свойства.
- •41. Теоремы о действиях над переменными величинами, имеющими конечные пределы.
- •42. Число e.
- •Содержание
- •Способы определения
- •Свойства
- •История
- •Приближения
- •43. Определение предела функции. Раскрытие неопределённостей.
- •44. Замечательные пределы, их вывод. Эквивалентные бесконечно малые величины.
- •Содержание
- •Первый замечательный предел
- •Второй замечательный предел
- •45. Односторонние пределы. Непрерывность и разрывы функции. Односторонние пределы
- •Левый и правый пределы функции
- •Точка разрыва первого рода
- •Точка разрыва второго рода
- •Точка устранимого разрыва
- •46. Определение производной. Геометрический смысл, механический смысл производной. Уравнения касательной и нормали к кривой и точке.
- •47. Теоремы о производной обратной, сложной функций.
- •48. Производные простейших элементарных функций.
- •49. Дифференцирование параметрических, неявных и степенно-показательных функций.
- •21. Дифференцирование неявных и параметрически заданных функций
- •21.1. Неявно заданная функция
- •21.2. Функция, заданная параметрически
- •50. Производные высших порядков. Формула Тейлора.
- •51. Дифференциал. Применение дифференциала к приближенным вычислениям.
- •52. Теоремы Ролля, Лагранжа, Коши. Правило Лопиталя.
- •53. Теорема о необходимом и достаточном условиях монотонности функции.
- •54. Определение максимума, минимума функции. Теоремы о необходимом и достаточном условиях существования экстремума функции.
- •Теорема (необходимое условие экстремума)
- •55. Выпуклость и вогнутость кривых. Точки перегиба. Теоремы о необходимом и достаточном условиях существования точек перегиба.
- •Доказательство
- •57. Определители n-ого порядка, их свойства.
- •58. Матрицы и действия над ними. Ранг матрицы.
- •Определение
- •Связанные определения
- •Свойства
- •Линейное преобразование и ранг матрицы
- •59. Обратная матрица. Теорема о существовании обратной матрицы.
- •60. Системы линейных уравнений. Матричное решение систем линейных уравнений. Правило Крамера. Метод Гаусса. Теорема Кронекера-Капелли.
- •Решение систем линейных алгебраических уравнений, методы решения, примеры.
- •Определения, понятия, обозначения.
- •Решение элементарных систем линейных алгебраических уравнений.
- •Решение систем линейных уравнений методом Крамера.
- •Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
- •Решение систем линейных уравнений методом Гаусса.
- •Решение систем линейных алгебраических уравнений общего вида.
- •Теорема Кронекера – Капелли.
- •Метод Гаусса для решения систем линейных алгебраических уравнений общего вида.
- •Запись общего решения однородных и неоднородных систем линейных алгебраических с помощью векторов фундаментальной системы решений.
- •Решение систем уравнений, сводящихся к слау.
- •Примеры задач, сводящихся к решению систем линейных алгебраических уравнений.
15. Способы задания прямой на плоскости.
Рассмотрим
несколько способов задания прямой на
плоскости. Прежде всего отметим, что
это линейные уравнения, т. е. такие
уравнения,
в которых переменные
![]() и
и![]() содержатся
только в первых степенях.
содержатся
только в первых степенях.
Уравнение
прямой с угловым коэффициентом
![]()
Сначала
исследуем прямую, которая задана
уравнением
![]() .
Эта прямая всегда проходит через начало
координат, т. е. через точку
.
Эта прямая всегда проходит через начало
координат, т. е. через точку![]() Коэффициент
Коэффициент![]() называется
угловым коэффициентом. Равен он тангенсу
угла наклона, образуемого прямой с
положительным направлением оси
называется
угловым коэффициентом. Равен он тангенсу
угла наклона, образуемого прямой с
положительным направлением оси![]() (рис.
4), т. е.
(рис.
4), т. е.![]() .
Если учесть, что тангенс острого угла
есть величина положительная, а тангенс
тупого угла – величина отрицательная,
то можно очень быстро представить
расположение прямой на плоскости.
.
Если учесть, что тангенс острого угла
есть величина положительная, а тангенс
тупого угла – величина отрицательная,
то можно очень быстро представить
расположение прямой на плоскости.
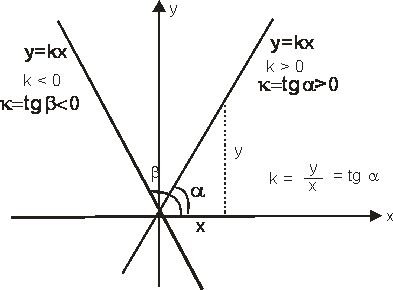
Рис.
4. Геометрический смысл углового
коэффициента
![]()
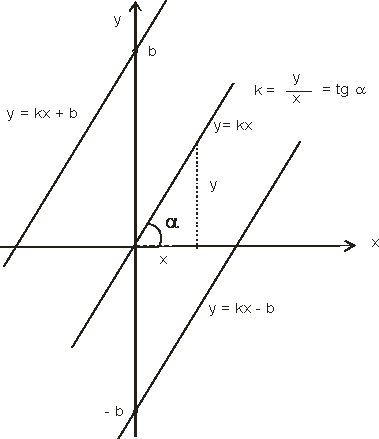
Рис.
5. Построение графика прямой
![]()
Прямая,
заданная уравнением
![]() ,
параллельна прямой, описанной уравнением
,
параллельна прямой, описанной уравнением![]() .
Коэффициент
.
Коэффициент![]() есть
величина отрезка, отсекаемого прямой
есть
величина отрезка, отсекаемого прямой![]() на
оси
на
оси![]() Эта
величина может быть как положительной,
так и отрицательной. Для того, чтобы
построить график прямой
Эта
величина может быть как положительной,
так и отрицательной. Для того, чтобы
построить график прямой![]() ,
зная график прямой
,
зная график прямой![]() ,
надо прямую
,
надо прямую![]() параллельно
поднять на величину
параллельно
поднять на величину![]() относительно
начала координат, если
относительно
начала координат, если![]() .
Если же величина
.
Если же величина![]() отрицательная,
тогда прямую
отрицательная,
тогда прямую![]() надо
параллельно опустить на величину
надо
параллельно опустить на величину![]() относительно
начала координат (рис. 5).
относительно
начала координат (рис. 5).
Общее уравнение прямой на плоскости
Линейное
уравнение вида
![]() называется
общим уравнением
прямой на плоскости.
называется
общим уравнением
прямой на плоскости.
Если
коэффициент
![]() ,
то прямая, уравнение которой в этом
случае записывается
,
то прямая, уравнение которой в этом
случае записывается![]() ,
проходит через начало координат.
,
проходит через начало координат.
Важную
роль выполняют коэффициенты
![]() .
Вектор
.
Вектор![]() ,
координатами которого являются эти
числа, называетсянормальным
вектором прямой, заданной уравнением
,
координатами которого являются эти
числа, называетсянормальным
вектором прямой, заданной уравнением
![]() .
.
Следует
обратить внимание на тот факт, что
![]()
это проекция нормального вектора
это проекция нормального вектора
![]() на
ось
на
ось![]()
![]()
это проекция нормального вектора
это проекция нормального вектора
![]() на
ось
на
ось![]()
Вектор
![]() ,
начало которого совпадает с началом
координат, задает общее расположение
прямой на плоскости: искомая прямая
перпендикулярна вектору
,
начало которого совпадает с началом
координат, задает общее расположение
прямой на плоскости: искомая прямая
перпендикулярна вектору![]() .
.
Взаимное расположение прямых на плоскости
На
плоскости заданы прямые
![]() общими
уравнениями:
общими
уравнениями:
![]()
Если
выполнены условия
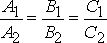 ,
то прямые
,
то прямые![]() совпадают.
совпадают.
Если
выполнены условия
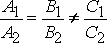 ,
то прямые
,
то прямые![]() параллельны.
параллельны.
Векторы
![]() нормальные
векторы прямых
нормальные
векторы прямых
![]() и
и![]() соответственно.
соответственно.
Если
скалярное произведение векторов
![]() и
и![]() обращается
в ноль, т. е.
обращается
в ноль, т. е.![]() то
прямые
то
прямые![]() и
и![]() перпендикулярны.
перпендикулярны.
Условие
перпендикулярности прямых
![]() и
и![]() в
координатной форме:
в
координатной форме:
|
| |
|
|
|
Уравнение прямой, проходящей через точку, с заданным угловым коэффициентом
На
плоскости дана точка
![]() .
Прямая, угловой коэффициент
.
Прямая, угловой коэффициент![]() которой
задан, проходит через эту точку
которой
задан, проходит через эту точку![]() (рис.
6). Уравнение ее имеет вид:
(рис.
6). Уравнение ее имеет вид:
|
| |
|
|
|
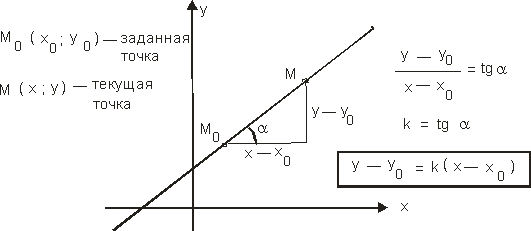
Рис.
6. Уравнение прямой, проходящей через
заданную точку
![]() ,
с заданным угловым коэффициентомk
,
с заданным угловым коэффициентомk
Уравнение прямой, проходящей через две заданные точки
На
плоскости даны две точки
![]() и
и
![]() .
Уравнение прямой, проходящей через эти
точки, очень легко написать. На прямой
возьмем текущую, т. е. любую, точку
.
Уравнение прямой, проходящей через эти
точки, очень легко написать. На прямой
возьмем текущую, т. е. любую, точку![]() .
Построим два вектора
.
Построим два вектора![]() и
и![]() .
По построению эти векторы коллинеарны.
Условие коллинерности – это
пропорциональность одноименных координат
векторов:
.
По построению эти векторы коллинеарны.
Условие коллинерности – это
пропорциональность одноименных координат
векторов: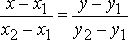 .
Это и есть искомое уравнение.
.
Это и есть искомое уравнение.
Преобразуем полученное равенство:
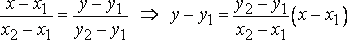
Заметим,
что отношение
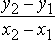 есть
ни что иное как угловой коэффициент
есть
ни что иное как угловой коэффициент![]() (рис.
7), т. е.
(рис.
7), т. е.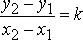 .
.
Возникает
вопрос:
изменится ли уравнение прямой, если
будем рассматривать векторы
![]() и
и![]() ?
Ведь в этом случае уравнение прямой
должны записать как
?
Ведь в этом случае уравнение прямой
должны записать как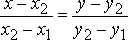 ,
или иначе
,
или иначе![]() [1].
[1].
Вывод. Уравнение
прямой, проходящей через две точки
![]() и
и![]() ,
имеет вид
,
имеет вид
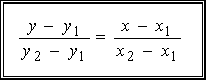
|
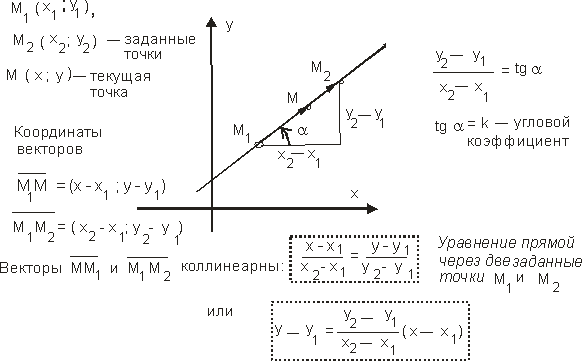
Рис. 7. Уравнение прямой, проходящей через две заданные точки М1 и М2
Примечание.
Уравнение прямой, проходящей через две
точки
![]() и
и![]() в
пространствеR3,
имеет вид
в
пространствеR3,
имеет вид
|
| |
|
|
|
Пример
41.
Найти нормальный вектор прямой
![]() .
.
Решение
Прямая
задана общим уравнением
![]() .
Она не проходит через начало координат.
Вектор
.
Она не проходит через начало координат.
Вектор![]() является
нормальным вектором прямой, а это
означает, что прямая перпендикулярна
вектору
является
нормальным вектором прямой, а это
означает, что прямая перпендикулярна
вектору![]()
Ответ:
![]() нормальный
вектор прямой.
нормальный
вектор прямой.
Примечание.
Общее уравнение прямой
![]() не
является самым удачным для ее
построения. Большей частью решение
задачи построения такой прямой сводят
к приведению общего уравнения к
уравнению с угловым коэффициентом
не
является самым удачным для ее
построения. Большей частью решение
задачи построения такой прямой сводят
к приведению общего уравнения к
уравнению с угловым коэффициентом![]() .
Однако есть одно красивое представление
прямой в виде так называемого уравнения
в «отрезках». Это уравнение позволяет
не только быстро построить прямую, но
и решить ряд других сопутствующих
задач.
.
Однако есть одно красивое представление
прямой в виде так называемого уравнения
в «отрезках». Это уравнение позволяет
не только быстро построить прямую, но
и решить ряд других сопутствующих
задач.
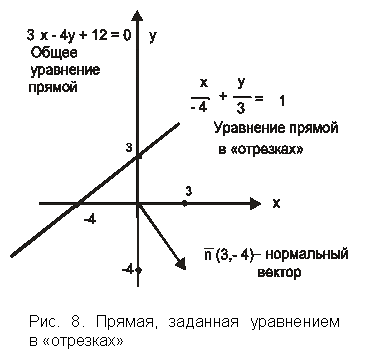
Уравнение прямой в «отрезках»
Предположим,
прямая задана общим уравнением
![]() .
Полагаем, что в уравнении коэффициент
.
Полагаем, что в уравнении коэффициент![]() .
В противном случае задача упрощается,
так как прямая проходит через начало
координат.
.
В противном случае задача упрощается,
так как прямая проходит через начало
координат.
Выполним
тождественные преобразования, проследите
за ними:
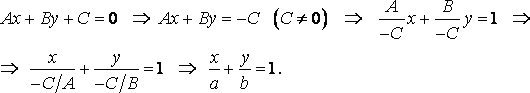
Здесь
введены обозначения:
![]() Обратите
внимание на уравнение
Обратите
внимание на уравнение![]() .
Это и есть уравнение прямой«в
отрезках». Возникает вопрос, где эти
отрезки?
.
Это и есть уравнение прямой«в
отрезках». Возникает вопрос, где эти
отрезки?
Величина
отрезка, который прямая
![]() отсекает
на оси
отсекает
на оси
![]() от
начала координат, равна
от
начала координат, равна![]() Действительно,
чтобы найти точку пересечения прямой
Действительно,
чтобы найти точку пересечения прямой![]() и
оси
и
оси![]() (
(![]() уравнение
оси
уравнение
оси
![]() ),
надо решить систему, содержащую уравнения
этих прямых:
),
надо решить систему, содержащую уравнения
этих прямых:
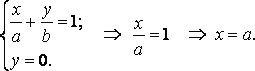
Аналогично
можно показать, что величина
отрезка, отсекаемого прямой
![]() на
оси
на
оси
![]() (
(![]() уравнение
оси
уравнение
оси
![]() )
от начала координат, равна
)
от начала координат, равна![]()
И
теперь, чтобы построить прямую, записанную
уравнением в
«отрезках», надо в прямоугольной системе
координат на оси
![]() от
начала координат отложить
отрезок
величины
от
начала координат отложить
отрезок
величины
![]() на
оси
на
оси![]() от
начала координат
отрезок величины
от
начала координат
отрезок величины
![]() и,
соединив их концы, получим искомый
график прямой.
и,
соединив их концы, получим искомый
график прямой.
В
уравнении
![]() дроби
дроби![]() и
и![]() должны
быть со знаками «+». Если появляются
знаки «»,
унесите их в знаменатели. Говорим, что
должны
быть со знаками «+». Если появляются
знаки «»,
унесите их в знаменатели. Говорим, что
![]() и
и![]()
это величины отрезков, а не длины. А это
значит, что
это величины отрезков, а не длины. А это
значит, что
![]() и
и![]() могут
быть не только положительными, но и
отрицательными.
могут
быть не только положительными, но и
отрицательными.
Пример
42.
Построить прямую
![]() .
.
|
Решение Что
можно сказать, глядя на заданное
уравнение? Информации достаточно.
Прямая описывается общим уравнением.
Свободный коэффициент не равен нулю
Приведем общее уравнение прямой к уравнению в «отрезках». Проследите за преобразованиями.
|
|