13. Векторное произведение векторов, его свойства. Площадь параллелограмма.

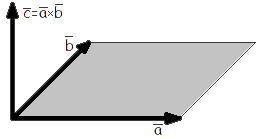
Векторным произведениемвектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах a и b, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора c (рис. 1).

рис. 1

Формулы вычисления векторного произведения векторов

Векторное произведениедвух векторов a = {a_x; a_y; a_z} и b = {b_x; b_y; b_z} в декартовой системе координат - это вектор, значение которого можно вычислить, используя следующие формулы:

a × b =	i	j	k	= i(aybz - azby) - j(axbz - azbx) + k(axby - aybx)
	ax	ay	az
	bx	by	bz

a × b = {a_yb_z- a_zb_y; a_zb_x- a_xb_z; a_xb_y- a_yb_x}

Свойства векторного произведения векторов

• Геометрический смысл векторного произведения.

Модуль векторного произведения двух векторов a и b равен площади параллелограмма построенного на этих векторах:

S_парал= a × b]

• Геометрический смысл векторного произведения.

Площадь треугольника построенного на векторах a и b равна половине модуля векторного произведения этих векторов:

SΔ =	1	|a × b|
	2

• Векторное произведения двух не нулевых векторов a и b равно нулю тогда и только тогда, когда вектора коллинеарны.

• Вектор c, равный векторному произведению не нулевых векторов a и b, перпендикулярен этим векторам.

• a × b = -b × a

• (k a) × b = a × (k b) = k (a × b)

• (a + b) × c = a × c + b × c

14. Смешанное произведение векторов, его свойства. Условие компланарности вектора. Объем параллелепипеда. Объём пирамиды.

Смешанным произведением некомпланарныхвекторов,взятых в данном порядке, называетсяобъём параллелепипеда, построенного на данных векторах, снабжённый знаком «+», если базисправый, и знаком «–», если базислевый.

1. Смешанное произведение не меняется при циклической перестановке его сомножителей (не меняется ни объем параллелепипеда, ни ориентация его ребер): .

2. Смешанное произведение не меняетсязнаков векторного и скалярного умножения:, поэтому смешанное произведение записывают.

3. Смешанное произведение меняет свой знак при перемене любых двух вектор-сомножителей: ,.

4. Смешанное произведение ненулевых векторов ,иравно нулю тогда и только тогда, когда они компланарны:,, – компланарны.

Доказательство. Предположим, что векторы ,и– не компланарны. Тогда можно построить параллелепипед имеющий объем, т.е., но это противоречит условию, согласно которого,. Следовательно, векторы,и– компланарны.

Обратно, пусть ,и– компланарны. Тогда вектори перпендикулярен плоскости, в которой находятся векторы,и, значит, он перпендикулярен любому вектору, лежащему в этой плоскости, напримерЭто значит, что .

Смешанное произведение векторов, заданных своими проекциями в декартовой системе координат.

Пусть векторы заданы своими разложениями по ортам в декартовой системе координат:

 

, и.

 

Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:

.

 

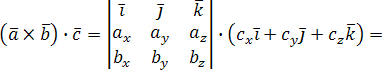
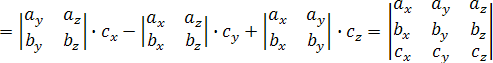Итак,

.

 

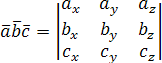Приложения смешанного произведения:

1. Определение взаимной ориентации векторов в пространстве.

Если ,и– правая тройка, еслилевая.

2. Установление компланарности векторов:

 

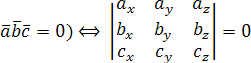
(  (,, – компланарны).

 

3. Определение объема параллелепипеда и треугольной пирамиды (тетраэдра):

, .

 

Пример. Компланарны ли векторы ,и, если .

Решение. Вычислим смешанное произведение векторов:

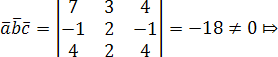векторы ,ине компланарны.

 

Пример. Доказать, что векторы ,икомпланарны.

Решение. Рассмотрим матрицу, составленную из координат векторов ,и 

 

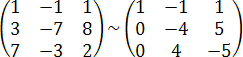, т. к. определитель матрицы равен нулю, то векторы линейно зависимы, следовательно они компланарны.

 

Пример. Вычислить объем тетраэдра с вершинами в точках и его высоту, опущенную из вершинына грань, если

Решение. Найдем координаты векторов:

, ,.

Вычислим объем:

.

 

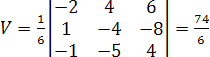Поскольку объем тетраэдра , то высота.

Вычислим площадь основания тетраэдра

.

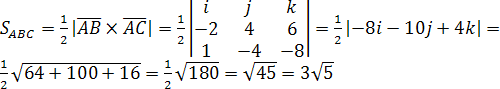Итак, высота .